Bu içeriği görüntülemek için JoVE aboneliği gereklidir. Oturum açın veya ücretsiz deneme sürümünü başlatın.
Research Article
Zaman Gecikmesini Dikkate Alan Manyetolojik Sönümleyicilere Dayalı Yapının Stokastik Yarı Aktif Kontrol Yöntemi
Bu Makalede
Özet
Bu yazıda, MR sönümleyiciler tarafından kontrol edilen yapıların güvenilirliğini korumak için tasarlanmış, zaman gecikmesi kompanzasyonlu bir Stokastik Optimal Yarı Aktif Kontrol yöntemi (SOSC-PSO) önerilmiştir.
Özet
Manyetorolojik (MR) sönümleyicilerin yarı aktif kontrol sistemlerinde kullanımı önemli bir zorlukla karşı karşıyadır: stokastik uyarımlar altında inşaat mühendisliği yapılarının güvenilirliğini azaltan geri besleme süreçlerinin neden olduğu zaman gecikmesi. Bu makale, bu sorunu ele almak ve yapısal güvenilirliği korumak için Fiziksel Stokastik Optimal kontrol teorisinden (PSO) yararlanarak, zaman gecikmesi telafisi (SOSC-PSO) ile bir Stokastik Optimal Yarı Aktif Kontrol yöntemi önermektedir. Önerilen yöntem, yarı aktif kontrol kuvvetini hem mevcut hem de önceki durumların bir fonksiyonu olarak türetir ve kontrol sürecindeki zaman gecikmelerini telafi eder. Kontrol etkinliğini optimize etmek için, temel parametreler sistem için bir güvenilirlik kriterine göre ayarlanır. Stokastik sismik uyarımlar altında tek serbestlik dereceli ve çok serbestlik dereceli yapılar üzerinde yapılan doğrulama analizleri, zaman gecikmelerinin MR sönümleyicilerin performansını önemli ölçüde bozduğunu göstermektedir. Bununla birlikte, zaman gecikmesi kompanzasyonlu SOSC-PSO yöntemi, kontrol etkinliğini önemli ölçüde artırır ve optimize edilmiş parametrelerle, yapısal kontrol sisteminin güvenilirliğini parametre optimizasyonu olmayan yöntemlerin ötesinde artırır.
Giriş
Depremler ve aşırı rüzgarlar gibi felaket olayları karşısında mühendislik yapılarının performansının iyileştirilmesi, inşaat mühendisliği topluluğu içinde birincil endişe kaynağı olmaya devam etmektedir. Titreşimleri azaltmak için etkili bir teknik olan yapısal kontrolün, bu tür yapıların hem güvenliğini hem de işlevselliğini arttırdığı kanıtlanmıştır 1,2,3. Son birkaç on yılda, bu amaç için çeşitli ileri yöntemler ve teknolojiler geliştirilmiştir. Bu yöntemler, kontrol cihazlarını çalıştırmak için kullanılan enerji türüne göre genel olarak dört kategoriye ayrılabilir: aktif, yarı aktif, pasif ve hibrit kontrol sistemleri 4,5,6,7.
Aktif kontrolde, gerekli kontrol kuvveti doğrudan kontrol cihazları aracılığıyla uygulanır ve bu da önemli miktarda enerji gerektirir 8,9,10. Yarı aktif kontrol ise, aktif sistemlere kıyasla çok daha az enerji gerektiren, kontrol sinyallerine dayalı olarak kontrol cihazlarının özelliklerinin (sönümleme veya sertlik gibi) ayarlanmasını içerir11. Pasif kontrol, aksine, sisteme herhangi bir harici enerji girişi olmadan enerji dağılımına dayanır 12,13,14. Hibrit sistemler, daha etkili performans elde etmek için aktif/yarı aktif ve pasif kontrol stratejilerinin özelliklerini birleştirir15. Bu yaklaşımlar arasında yarı aktif kontrol, düşük enerji tüketimi ve yüksek verimlilik dengesi nedeniyle özellikle umut verici olarak kabul edilmektedir 16,17,18. Manyetolojik (MR) sönümleyici, üstün dinamik sönümleme özellikleri ile en etkili yarı aktif kontrol cihazlarından biri olarak kabul edilmektedir 19,20,21,22.
Bununla birlikte, MR damperlerini kullanan yarı aktif kontrol sistemlerinde bir zorluk ortaya çıkar, çünkü geri besleme mantığı kaçınılmaz olarak zaman gecikmelerine neden olur. Bu gecikmelere tipik olarak aşağıdakiler dahil olmak üzere çeşitli faktörler 23,24,25 neden olur: (i) sensör verilerinin alınması ve işlenmesi, (ii) kontrolör26 tarafından gerekli kontrol kuvvetinin hesaplanması, (iii) transdüserler aracılığıyla MR damperlerine27 sinyal iletimi ve (iv) MR damperlerinin kendileri tarafından gerçek kuvvet üretimi28. Bu tür zaman gecikmeleri, üretilen kontrol kuvveti ile yapı tarafından beklenen kuvvet arasında tutarsızlıklara yol açabilir ve kontrol etkinliğini önemli ölçüde tehlikeye atabilir29. Ne yazık ki, MR damperleri için mevcut kontrol algoritmalarının çoğu bu gecikmeleri hesaba katmamaktadır.
Ek olarak, katastrofik olayların doğal rastgeleliği nedeniyle, herhangi bir etkili yarı aktif kontrol algoritması, stokastik uyarımlar altında performansı koruyabilmelidir. Klasik bir stokastik optimizasyon tekniği olan Doğrusal Kuadratik Gauss (LQG) kontrol yöntemi, MR damperleri ile donatılmış yapılarda titreşimleri azaltmak için araştırılmıştır. Örneğin, Dyke ve ark. hızlanma geri beslemesi30 kullanarak MR damperleri ile donatılmış yapıların sismik tepkisini iyileştirmek için bir LQG kırpılmış-optimal kontrol stratejisi önerdi. Ying ve ark. MR sönümleyicili doğrusal olmayan yapılar için stokastik ortalama alma ve dinamik programlama tekniklerini içeren, kırpılmamış yarı aktif stokastik optimal kontrol stratejisini tanıttı31. Diğer çalışmalar, taban yalıtımlı binaların19 sismik performansını artırmak için modal tabanlı LQG kontrolü uygulamış ve rüzgar türbini kulelerinde32 titreşim azaltma için etkinliğini analiz etmiştir. Bununla birlikte, beyaz Gauss gürültüsünü varsayan klasik LQG yöntemleri, depremler veya kuvvetli rüzgarlar gibi gerçek dünya uyarımlarının durağan olmayan, Gauss olmayan doğasını modellemek için pek uygun değildir. Bunu ele almak için, geleneksel LQG yöntemlerinin sınırlamalarının üstesinden gelen ve çeşitli stokastik uyarımları ele almak için daha doğru bir çerçeve sunan fiziksel tabanlı stokastik optimal (PSO) kontrol kavramıgeliştirilmiştir 33,34 35. Çalışmalar, PSO tabanlı yarı aktif stokastik optimal kontrolün, stokastik sismik kuvvetlere maruz kalan hem doğrusal hem de doğrusal olmayan yapılar için titreşim azaltmayı önemli ölçüde iyileştirdiğini göstermiştir36.
Bu nedenle, MR damperleri25,37 tarafından kontrol edilen yapıların güvenilirliğini artıran, zaman gecikmelerini telafi eden sağlam bir yarı aktif kontrol yöntemine acil ihtiyaç vardır. Ayrıca, stokastik uyarımlar altında optimum kontrol performansını sağlamak için, önerilen kontrol yönteminin kritik parametrelerini güvenilirliğe dayalı bir yaklaşım kullanarak optimize etmek esastır. Bu nedenle, MR sönümleyicilere sahip yapıların güvenilirliğini artırmak için bu yazıda zaman gecikmesi kompanzasyonlu bir Stokastik Optimal Yarı Aktif Kontrol yöntemi (SOSC-PSO) önerilmiştir.
Protokol
1. Stokastik optimal yarı aktif kontrol yöntemi
Bir MR damperinin kontrol etkisi, kaçınılmaz zaman gecikmesinden önemli ölçüde etkilendiğinden, kontrol edilen yapının performansını artırmak için zaman gecikmesi kompanzasyon algoritmasına sahip yarı aktif bir kontrol yöntemi geliştirilmiştir. Ayrıca, dış uyarımların doğasında bulunan rastgelelik, dinamik tepkilerin bariz belirsizliklerine neden olur. PSO kontrolü, yapı kontrol sisteminin güvenilirliğini sağlamak için önerilen yöntemin kritik parametrelerini optimize etmek için tanıtıldı.
1.1 Yarı aktif kontrolün kompanzasyon algoritması
Genellik kaybı olmadan, stokastik uyarımlara tabi hareket denkleminin şu şekilde verildiği, zaman gecikmeli MR sönümleyicileri tarafından kontrol edilen bir n-Serbestlik Derecesi (n-DOF) yapısını düşünün:
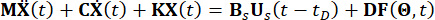 (1)
(1)
Burada  yapının sırasıyla n x n kütle, sönümleme ve sertlik matrislerini temsil eder; n, kontrol edilen yapının serbestlik derecesi sayısını temsil eder. Yapının yer değiştirme, hız ve ivme vektörleri sırasıyla ile temsil
yapının sırasıyla n x n kütle, sönümleme ve sertlik matrislerini temsil eder; n, kontrol edilen yapının serbestlik derecesi sayısını temsil eder. Yapının yer değiştirme, hız ve ivme vektörleri sırasıyla ile temsil 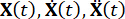 edilir. Sembollerin üzerindeki küçük bir ve iki nokta, birinci ve ikinci kez türevleri temsil eder. Us (t - tD), MR damperlerinin zaman gecikmeli kontrol kuvvetinin r boyutlu vektörünü temsil eder ve r, damper sayısını temsil eder; t zamanı temsil eder; tD , bu çalışmadaki tüm sönümleyiciler arasında aynı olduğu varsayılan zaman gecikmesini ifade eder, burada
edilir. Sembollerin üzerindeki küçük bir ve iki nokta, birinci ve ikinci kez türevleri temsil eder. Us (t - tD), MR damperlerinin zaman gecikmeli kontrol kuvvetinin r boyutlu vektörünü temsil eder ve r, damper sayısını temsil eder; t zamanı temsil eder; tD , bu çalışmadaki tüm sönümleyiciler arasında aynı olduğu varsayılan zaman gecikmesini ifade eder, burada 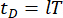 , burada integral sayısı
, burada integral sayısı  ile ve
ile ve  örnekleme periyodunu belirtir.
örnekleme periyodunu belirtir. 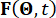 stokastik uyarımların p boyutlu vektörünü temsil eder ve
stokastik uyarımların p boyutlu vektörünü temsil eder ve  dış uyarımlarla ilişkili rastgeleliği karakterize eden stokastik parametre vektörünü temsil eder. Boyutu,
dış uyarımlarla ilişkili rastgeleliği karakterize eden stokastik parametre vektörünü temsil eder. Boyutu,  dış uyarımlar için kullanılan modele bağlıdır, ancak yapının mekanik serbestlik dereceleri ile ilgili değildir. Bs ve D , sırasıyla damperlerin ve harici uyarımların konumlarını belirten n x r ve n x p matrisleridir. Durum uzayı gösteriminde, Eşitlik (1) şu şekilde yazılır:
dış uyarımlar için kullanılan modele bağlıdır, ancak yapının mekanik serbestlik dereceleri ile ilgili değildir. Bs ve D , sırasıyla damperlerin ve harici uyarımların konumlarını belirten n x r ve n x p matrisleridir. Durum uzayı gösteriminde, Eşitlik (1) şu şekilde yazılır:
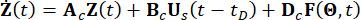 (2)
(2)
Burada 2n boyutlu durum vektörünü temsil eder 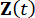 ;
; 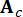 2n x 2n sistem matrisini temsil eder;
2n x 2n sistem matrisini temsil eder; 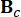 MR sönümleyicilerin 2n x r konum matrisini temsil eder;
MR sönümleyicilerin 2n x r konum matrisini temsil eder; 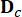 Dış uyarımların 2N x P konum matrisini temsil eder. Bu parametreler şu şekilde ifade edilir:
Dış uyarımların 2N x P konum matrisini temsil eder. Bu parametreler şu şekilde ifade edilir:
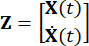 ,
, 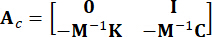 ,
, 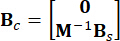 , (
, (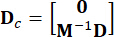 3)
3)
Nerede  , aynı sıraya sahip bir özdeşlik matrisini
, aynı sıraya sahip bir özdeşlik matrisini 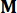 belirtir. Hesaplama kolaylığı için, sürekli durum uzayı denklemi Eşitlik (2) ayrık biçimde şu şekilde ifade edilebilir:
belirtir. Hesaplama kolaylığı için, sürekli durum uzayı denklemi Eşitlik (2) ayrık biçimde şu şekilde ifade edilebilir:
 (4)
(4)
Zaman noktasının  olarak basitleştirildiği
olarak basitleştirildiği 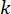 yer. Ve
yer. Ve  ,
, 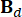 ,
, 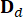 2n x 2n, 2n x r ve 2n x p matrislerini gösterir, bunlar şu şekilde ifade edilir:
2n x 2n, 2n x r ve 2n x p matrislerini gösterir, bunlar şu şekilde ifade edilir:
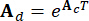 ,
, 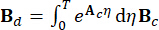 , (
, (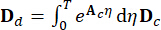 5)
5)
Nerede 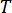 , örnekleme dönemini belirtir.
, örnekleme dönemini belirtir.
Aktif kontrol ile benzer etkinliği elde etmek için, zaman gecikmeli MR damper tabanlı kontrol için Hrovat algoritmasına38 dayalı basit ve verimli bir kontrol yöntemi önerilmiştir:
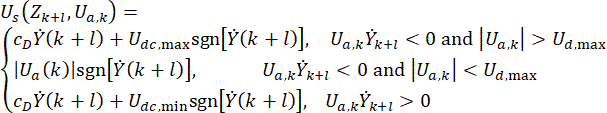 (6)
(6)
burada 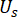 MR damperi için \ zaman noktasında\
MR damperi için \ zaman noktasında\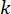 yarı aktif kontrol kuvveti sinyalini temsil eder;
yarı aktif kontrol kuvveti sinyalini temsil eder; 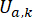 zaman gecikmesi telafisi ile referans aktif kontrol kuvvetini temsil eder;
zaman gecikmesi telafisi ile referans aktif kontrol kuvvetini temsil eder;  MR damperinin değiştirilebilir olan maksimum sönümleme kuvvetini temsil eder;
MR damperinin değiştirilebilir olan maksimum sönümleme kuvvetini temsil eder; 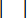 mutlak değer işlem sembolünü temsil eder;
mutlak değer işlem sembolünü temsil eder; 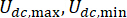 MR damperinin maksimum ve minimum Coulombic kuvvetlerini temsil eder;
MR damperinin maksimum ve minimum Coulombic kuvvetlerini temsil eder; 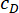 viskoz sönümleme katsayısını temsil eder;
viskoz sönümleme katsayısını temsil eder; 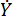 pistonun damper silindirine göre hareket hızı olan MR damperindeki hız girişini temsil eder. Eşitlik (6)'da,
pistonun damper silindirine göre hareket hızı olan MR damperindeki hız girişini temsil eder. Eşitlik (6)'da, 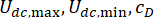 MR damperinin tasarlanmış parametrelerini temsil edin.
MR damperinin tasarlanmış parametrelerini temsil edin.
Denklem (6), MR damperinin yarı aktif kontrol kuvvetinin zaman gecikmeli olarak hesaplanmasını gösterir. Denklem (4)'teki zaman adımındaki 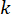 yarı aktif kontrol kuvvetinin
yarı aktif kontrol kuvvetinin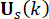 , zaman adımındaki
, zaman adımındaki 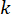 aktif kontrol kuvveti
aktif kontrol kuvveti  ve zaman adımındaki
ve zaman adımındaki 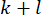 durum değişkenine
durum değişkenine 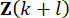
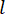 dayalı olarak hesaplandığı görülmektedir. Aktif kontrol kuvvetini
dayalı olarak hesaplandığı görülmektedir. Aktif kontrol kuvvetini  elde etmek için, geleneksel maliyet fonksiyonu şu şekilde belirlenir:
elde etmek için, geleneksel maliyet fonksiyonu şu şekilde belirlenir:
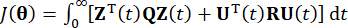 (7)
(7)
Burada  sistem durumunun 2n x 2n simetrik pozitif yarı kesin ağırlıklandırma matrisini temsil eder;
sistem durumunun 2n x 2n simetrik pozitif yarı kesin ağırlıklandırma matrisini temsil eder; 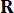 kontrol kuvvetinin r x r simetrik pozitif belirli ağırlıklandırma matrisini temsil eder. Dış uyarımın yok denecek kadar az olduğu görülmektedir. Aslında, Eşitlik (7)'ye dayanarak, yapı kontrol sistemi, harici uyarma türü ne olursa olsun optimum kontrol etkisini elde edebilir. Ayrık form olarak, Eşitlik (7)39 olarak ifade edilir:
kontrol kuvvetinin r x r simetrik pozitif belirli ağırlıklandırma matrisini temsil eder. Dış uyarımın yok denecek kadar az olduğu görülmektedir. Aslında, Eşitlik (7)'ye dayanarak, yapı kontrol sistemi, harici uyarma türü ne olursa olsun optimum kontrol etkisini elde edebilir. Ayrık form olarak, Eşitlik (7)39 olarak ifade edilir:
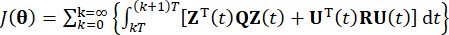 (8)
(8)
Maliyet fonksiyonunun  en aza indirilmesi, koşullu bir aşırı değer problemine yol açar ve aktif kontrol kuvveti
en aza indirilmesi, koşullu bir aşırı değer problemine yol açar ve aktif kontrol kuvveti 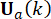 25 ile hesaplanır:
25 ile hesaplanır:
 (9)
(9)
Burada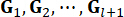 , ağırlıklandırma matrisleri ve 37 tarafından belirlenen, zaman adımındaki
, ağırlıklandırma matrisleri ve 37 tarafından belirlenen, zaman adımındaki 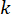 durum değişkeni
durum değişkeni 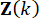 ve
ve 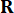 zaman adımındaki
zaman adımındaki  aktif kontrol kuvveti
aktif kontrol kuvveti 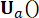 için kontrol kazançlarını
için kontrol kazançlarını 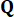 belirtin. Kaçınılmaz zaman gecikmesi nedeniyle, elde edilen kontrol kuvveti
belirtin. Kaçınılmaz zaman gecikmesi nedeniyle, elde edilen kontrol kuvveti  yapıya zaman noktalarında
yapıya zaman noktalarında 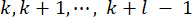 etki eder. Bu nedenle, Eşitlik (9)'daki aktif kontrol kuvveti şu şekilde hesaplanır:
etki eder. Bu nedenle, Eşitlik (9)'daki aktif kontrol kuvveti şu şekilde hesaplanır:
 (10) buyurmuştur.
(10) buyurmuştur.
Kavramın netliği için, Denklem (10)'daki yarı aktif kontrol kuvveti, Denklem (6)'ya dayalı olarak aşağıdaki gibi ifade edilir:
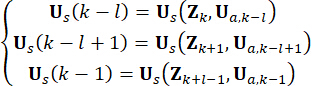 (11)
(11)
Nerede 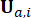 , zaman noktasındaki
, zaman noktasındaki  aktif kontrol kuvvetini belirtir. Eşitlik (11)'i Eşitlik (10) ile değiştirmek,
aktif kontrol kuvvetini belirtir. Eşitlik (11)'i Eşitlik (10) ile değiştirmek,
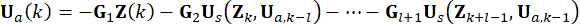 (12) buyurmuştur.
(12) buyurmuştur.
NOT: Hesaplama  için zaman noktasından
için zaman noktasından 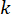 itibaren
itibaren 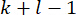 tüm durum
tüm durum  değerleri gereklidir. Bu nedenle, aşağıdaki durum tahmin yöntemitanıtılmıştır 40.
değerleri gereklidir. Bu nedenle, aşağıdaki durum tahmin yöntemitanıtılmıştır 40.
 (13)
(13)
Nerede , tahmin edilen değişkeni belirtir. Eşitlik (13) yinelemesi ile, 'deki
, tahmin edilen değişkeni belirtir. Eşitlik (13) yinelemesi ile, 'deki 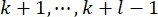 durum
durum  hesaplanır. Aktif kontrol kuvveti Ua(k) şu şekilde ifade edilir:
hesaplanır. Aktif kontrol kuvveti Ua(k) şu şekilde ifade edilir:
 (14) buyurmuştur.
(14) buyurmuştur.
Yarı aktif kontrol kuvveti, Eqs'in birleştirilmesiyle elde edilebilir. (6), (12) ve (13).
1.2 Yapı kontrol sisteminin güvenilirlik analizi
Olasılık koruma ilkesine göre, artırılmış sistem 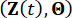 ve
ve  MR sönümleyicili yapı olasılık korunur ve aşağıdaki genelleştirilmiş olasılık yoğunluk evrimi denklemleri (GDEE'ler)38 tarafından yönetilir:
MR sönümleyicili yapı olasılık korunur ve aşağıdaki genelleştirilmiş olasılık yoğunluk evrimi denklemleri (GDEE'ler)38 tarafından yönetilir:
 (15) buyurmuştur.
(15) buyurmuştur.
 (16) buyurmuştur.
(16) buyurmuştur.
Burada  ,
, 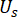 sırasıyla sistem durumunun ve yarı aktif kontrol kuvvetinin karşılık gelen bileşenlerini ve zaman gecikmeli olarak belirtir;
sırasıyla sistem durumunun ve yarı aktif kontrol kuvvetinin karşılık gelen bileşenlerini ve zaman gecikmeli olarak belirtir;  ve
ve 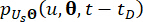 artırılmış örnek sistemlerinin
artırılmış örnek sistemlerinin 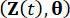 ortak olasılık yoğunluk fonksiyonlarını belirtir ve
ortak olasılık yoğunluk fonksiyonlarını belirtir ve  sırasıyla;
sırasıyla;  'nin
'nin  örnek uzayı içindeki örneği belirtir;
örnek uzayı içindeki örneği belirtir; 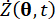 ve
ve 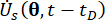 ) sırasıyla sistem durumu ve yarı aktif kontrol kuvveti bileşenlerinin birinci dereceden zaman kısmi türevlerini belirtir. Ortak olasılık yoğunluk fonksiyonları
) sırasıyla sistem durumu ve yarı aktif kontrol kuvveti bileşenlerinin birinci dereceden zaman kısmi türevlerini belirtir. Ortak olasılık yoğunluk fonksiyonları  ve
ve 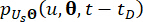 Eqs çözülerek elde edilebilir. (15) ve (16) aşağıdaki başlangıç koşullarıyla:
Eqs çözülerek elde edilebilir. (15) ve (16) aşağıdaki başlangıç koşullarıyla:
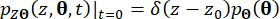 (17) buyurmuştur.
(17) buyurmuştur.
 (18) buyurmuştur.
(18) buyurmuştur.
Burada  Dirac delta fonksiyonunu gösterir;
Dirac delta fonksiyonunu gösterir; 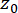 ve
ve 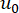 'nin
'nin 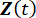 deterministik başlangıç değerlerini sırasıyla belirtir
deterministik başlangıç değerlerini sırasıyla belirtir 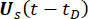 ;
;  örneğin
örneğin 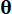 olasılık yoğunluk fonksiyonunu belirtir.
olasılık yoğunluk fonksiyonunu belirtir.
Anlık olasılık yoğunluk fonksiyonları 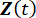 ve
ve 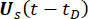 örnek uzayın alanının tek boyutlu integrali
örnek uzayın alanının tek boyutlu integrali 
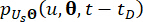 ile elde edilebilir:
ile elde edilebilir:
 (19) buyurmuştur.
(19) buyurmuştur.
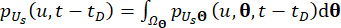 (20) buyurmuştur.
(20) buyurmuştur.
Nerede 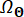 , 'nin
, 'nin  dağıtım etki alanını belirtir.
dağıtım etki alanını belirtir.
Eqs'ye dayalıdır. (19) ve (20), ilgili fiziksel büyüklüklerin tam olasılıksal bilgilerinin, algoritma parametreleriyle ilişkili ilişkileri tanımlandığı takdirde, kolayca türetildiği görülmektedir. İlgili fiziksel büyüklüklerin güvenilirliği, aşağıdaki ilgili performans fonksiyonu ile hesaplanabilir:
 (21) buyurmuştur.
(21) buyurmuştur.
 (22) buyurmuştur.
(22) buyurmuştur.
Burada 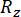 ve
ve 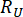 sırasıyla ilgili durum miktarının ve yarı aktif kontrol kuvvetinin hesaplanan güvenilirliğini belirtir;
sırasıyla ilgili durum miktarının ve yarı aktif kontrol kuvvetinin hesaplanan güvenilirliğini belirtir; 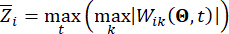 kontrol edilen yapının i'inci ilgili fiziksel miktarının eşdeğer uç değer vektörünü belirtir;
kontrol edilen yapının i'inci ilgili fiziksel miktarının eşdeğer uç değer vektörünü belirtir; 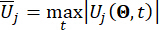 j'inci kontrol kuvvetinin eşdeğer uç değer vektörünü belirtir; sembollerdeki '-' şapkası, eşdeğer aşırı değer vektörünü41 gösterir;
j'inci kontrol kuvvetinin eşdeğer uç değer vektörünü belirtir; sembollerdeki '-' şapkası, eşdeğer aşırı değer vektörünü41 gösterir; 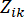 kontrol edilen yapının k'inci DOF'unun i'inci ilgili fiziksel miktarını belirtir;
kontrol edilen yapının k'inci DOF'unun i'inci ilgili fiziksel miktarını belirtir; 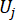 J-inci kontrol kuvvetini belirtir;
J-inci kontrol kuvvetini belirtir;  ,
, 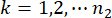 ,
, 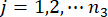 ,
,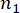 ,
, 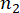 ve
ve 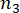 sırasıyla yapının ve yapıya monte edilen MR damperlerinin ilgili fiziksel büyüklüklerinin ve DOF'unun sayısını belirtir.
sırasıyla yapının ve yapıya monte edilen MR damperlerinin ilgili fiziksel büyüklüklerinin ve DOF'unun sayısını belirtir. 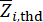 ve
ve  ve
ve  eşiklerini
eşiklerini 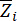 gösterir;
gösterir;  rastgele olayın olasılığını belirtir.
rastgele olayın olasılığını belirtir.
1.3 Parametrelerin optimizasyonu
Genliklerinin  oranı ve
oranı ve 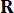 geri besleme kontrol modalitesinde kontrol etkinliğini38 yüksek oranda etkiler. Bu nedenle, en iyi kontrol etkinliğini
geri besleme kontrol modalitesinde kontrol etkinliğini38 yüksek oranda etkiler. Bu nedenle, en iyi kontrol etkinliğini elde etmek ve
elde etmek ve 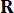 optimize etmek gerekir. Ayrıca, MR damper tabanlı bir kontrol yöntemi olarak, kontrol etkinliği de Eşitlik (6)'daki cihaz parametrelerinden
optimize etmek gerekir. Ayrıca, MR damper tabanlı bir kontrol yöntemi olarak, kontrol etkinliği de Eşitlik (6)'daki cihaz parametrelerinden 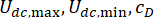 etkilenir. Yapı kontrol sisteminin optimal güvenilirliğini elde etmek için, güvenilirliğe dayalı kriter Eşitlik (25)'te önerilmiştir.
etkilenir. Yapı kontrol sisteminin optimal güvenilirliğini elde etmek için, güvenilirliğe dayalı kriter Eşitlik (25)'te önerilmiştir.

Şekil 1: Zaman gecikmesi kompanzasyonu ile stokastik optimal yarı aktif yapı kontrolü için parametre optimizasyonunun akış şeması. Kısaltmalar: GDEE = Olayın genelleştirilmiş diferansiyel denklemi ; PDF = Olasılık yoğunluk fonksiyonu. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Özetle, zaman gecikmesi kompanzasyonu ile MR sönümleyicilere dayalı stokastik optimal yarı aktif yapı kontrolünü gerçekleştirmek için iki aşama gereklidir:
1.3.1 Eşitlik (7)'de gösterilen maliyet fonksiyonunun  en aza indirilmesiyle, numuneler anlamında durum geri besleme mantığı elde edilir, yani Eşitlik 12)
en aza indirilmesiyle, numuneler anlamında durum geri besleme mantığı elde edilir, yani Eşitlik 12)
1.3.2 Güvenilirliğe dayalı performans fonksiyonunun  en aza indirilmesiyle, istatistik anlamında en uygun parametreler elde edilir. Şekil 1, adım 1.3.2'deki kontrolörün parametrelerinin optimizasyon akış şemasını sunar.
en aza indirilmesiyle, istatistik anlamında en uygun parametreler elde edilir. Şekil 1, adım 1.3.2'deki kontrolörün parametrelerinin optimizasyon akış şemasını sunar.
İki döngü katmanı içeren adım 1.3.2'deki aşağıdaki adımlar aşağıdaki gibidir:
1.3.2.1 Stokastik parametre vektörü 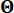 ile karakterize edilen stokastik uyarımların olasılık atanmış uzayının bölümlenmesi, ilişkili atanmış olasılıklarla birlikte bir dizi temsili noktanın
ile karakterize edilen stokastik uyarımların olasılık atanmış uzayının bölümlenmesi, ilişkili atanmış olasılıklarla birlikte bir dizi temsili noktanın  tanımlanmasına izin verirPq'lar. Bu yaklaşım, olarak gösterilen stokastik uyarma için numune süreçlerinin verimli bir şekilde oluşturulmasını sağlar, kolayca
tanımlanmasına izin verirPq'lar. Bu yaklaşım, olarak gösterilen stokastik uyarma için numune süreçlerinin verimli bir şekilde oluşturulmasını sağlar, kolayca 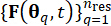 elde edilebilir.
elde edilebilir.
1.3.2.2 Yarı aktif yapı kontrol sisteminin parametre optimizasyonu için, maliyet-fonksiyon ağırlıklarının  değerlerini başlatın veya güncelleyin ve
değerlerini başlatın veya güncelleyin ve 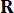 . Zaman gecikmeli ilişkili durum geri besleme kontrol kuvveti, bakınız Eşitlik (12), daha sonra hesaplanır.
. Zaman gecikmeli ilişkili durum geri besleme kontrol kuvveti, bakınız Eşitlik (12), daha sonra hesaplanır.
1.3.2.3 Eqs'de gösterilen GDEE'leri çözerek yapısal tepkilerin ve kontrol kuvvetinin olasılık yoğunluk fonksiyonlarının (PDF'ler) elde edilmesi. (17)–(20):
Optimizasyon çevrimdışıdır, tamamlanır ancak çevrimiçi değildir. Önerilen yöntemin gerçek yapı kontrol sistemlerinde uygulanabilirliğinde, optimal  ve
ve 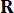 ulaşılabilir hale getirilmiştir ve gerçek uygulanabilir süreçte optimizasyona ihtiyaç duyulmamaktadır.
ulaşılabilir hale getirilmiştir ve gerçek uygulanabilir süreçte optimizasyona ihtiyaç duyulmamaktadır.
Numune uyarımına tabi tutulan yarı aktif yapı kontrol sisteminin deterministik dinamik analizi, bu sayede ilgili fiziksel büyüklükler 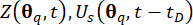 ve türevleri
ve türevleri  hesaplanmıştır.
hesaplanmıştır.
Toplam Varyasyon Azaltma (TVD) özelliklerine sahip modifiye edilmiş Lax-Wendroff şeması gibi bir sonlu fark yöntemi kullanılarak, Genelleştirilmiş Diferansiyel Denklemler (GDEE'ler) çözülebilir ve ortak olasılık yoğunluk fonksiyonları 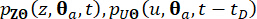 için sayısal çözümler türetilebilir.
için sayısal çözümler türetilebilir.
Deterministik dinamik analiz ve sonlu farklar yönteminin yukarıdaki iki adımını tekrarlayarak ve tüm temsili noktaların 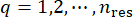 üzerinden geçerek, olasılık yoğunluk fonksiyonları toplama ile elde edilebilir:
üzerinden geçerek, olasılık yoğunluk fonksiyonları toplama ile elde edilebilir:
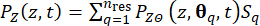 (23) buyurmuştur.
(23) buyurmuştur.
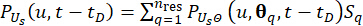 (24)
(24)
Nerede 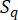 , örnek noktasıyla
, örnek noktasıyla  ilişkili alt etki alanının alan ölçüsünü temsil eder. Olayın Genelleştirilmiş Diferansiyel Denklemini (GDEE) çözmek için kullanılan yöntem, olasılık yoğunluk evrimi yöntemi (PDEM)42 olarak bilinir.
ilişkili alt etki alanının alan ölçüsünü temsil eder. Olayın Genelleştirilmiş Diferansiyel Denklemini (GDEE) çözmek için kullanılan yöntem, olasılık yoğunluk evrimi yöntemi (PDEM)42 olarak bilinir.
1.3.2.4 İlgili fiziksel büyüklüklerin PDF'leri, güvenilirliklerini değerlendirmek için kullanılır ve bunlar daha sonra olasılık kriterinin performans fonksiyonuna  dahil edilir.
dahil edilir.
1.3.2.5 Parametre optimizasyon süreci için sonlandırma kriterlerinin karşılanıp karşılanmadığını değerlendirin. Koşullar yerine getirilmezse, Adım 1.3.2.2'ye dönün; Eğer öyleyse, zaman gecikmeli kontrol sistemi için en uygun parametreler belirlenebilir. Bu çalışmada, parametre optimizasyonu için parametre güncellemelerini kolaylaştıran ve sonlandırma koşullarını tanımlayan MATLAB'daki genetik algoritma (GA) araç kutusu kullanılmıştır. Genetik algoritma ile, optimal değerler on yineleme içinde elde edilebilir ve yakınsama, yerel minimumma sorunları olmadan stabildir. GA'nın hesaplama maliyeti, parçacık sürüsü optimizasyonundan veya gradyan tabanlı yöntemlerden daha büyük olmasına rağmen, GA, bu makaledeki gibi karmaşık ve farklılaştırılamayan problemlerle başa çıkmada iyidir. Bu nedenle, GA uygulanır. Ve hızlı yakınsama özelliğinden dolayı, GA'nın hesaplama maliyeti kabul edilebilir.
1.3.2.6 Optimum güvenilirlik kontrolünü elde etmek için aşağıdaki performans fonksiyonu  formüle edilmiştir. Parametrelerin
formüle edilmiştir. Parametrelerin 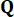 optimal değerlerini belirlemek için simge durumuna küçültün
optimal değerlerini belirlemek için simge durumuna küçültün  ve
ve :
:
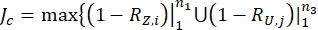 } (25)
} (25)
 (26) buyurmuştur.
(26) buyurmuştur.
Daha önce bahsedildiği gibi, kontrolörün ağırlıklandırma matrisleri simetriktir, burada matristeki 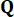 elemanlar yer değiştirmeye, hıza ve bunların etkileşimine atanan ağırlıklara karşılık gelirken, matristeki
elemanlar yer değiştirmeye, hıza ve bunların etkileşimine atanan ağırlıklara karşılık gelirken, matristeki  elemanlar kontrol kuvveti ile ilgili ağırlıkları temsil eder. Daha önceki çalışmalardan elde edilen bulgulara38 dayanarak, maliyet-fonksiyon ağırlıklarının
elemanlar kontrol kuvveti ile ilgili ağırlıkları temsil eder. Daha önceki çalışmalardan elde edilen bulgulara38 dayanarak, maliyet-fonksiyon ağırlıklarının 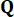 konfigürasyonlarının değiştirilmesinin ve
konfigürasyonlarının değiştirilmesinin ve  kontrol etkinliği üzerinde minimum etkiye sahip olduğu görülmüştür. Sonuç olarak, bu çalışmada aşağıda özetlendiği gibi basitleştirilmiş bir konfigürasyon benimsenmiştir:
kontrol etkinliği üzerinde minimum etkiye sahip olduğu görülmüştür. Sonuç olarak, bu çalışmada aşağıda özetlendiği gibi basitleştirilmiş bir konfigürasyon benimsenmiştir:
 ,
,  (27)
(27)
Nerede 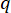 , tanımlanacak durum ağırlıklandırma matrisinin katsayısını belirtir;
, tanımlanacak durum ağırlıklandırma matrisinin katsayısını belirtir; 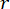 tanımlanacak kontrol ağırlıklandırma matrisinin katsayısını belirtir;
tanımlanacak kontrol ağırlıklandırma matrisinin katsayısını belirtir;  özdeşlik matrisini belirtir. Kontrol etkisi, değerlerin kendilerinden
özdeşlik matrisini belirtir. Kontrol etkisi, değerlerin kendilerinden 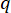 değil, oranından
değil, oranından 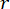 etkilenir. Ayrıca,
etkilenir. Ayrıca, 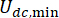 Denklem (6), MR damperinin minimum Coulombic kuvvetini belirtir, bu da damperdeki akım girişinin sıfır olduğu anlamına gelir
Denklem (6), MR damperinin minimum Coulombic kuvvetini belirtir, bu da damperdeki akım girişinin sıfır olduğu anlamına gelir 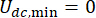 . Daha sonra, Eşitlik (26) şu şekilde daha da ifade edilebilir: T
. Daha sonra, Eşitlik (26) şu şekilde daha da ifade edilebilir: T
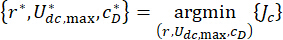 (28) buyurmuştur.
(28) buyurmuştur.
En uygun endişe katsayıları nerede 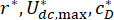 . Mühendislikte makul hale getirmek için, optimum aralıkları MR damper fabrikalarının üretim kapasitesine dayanmaktadır.
. Mühendislikte makul hale getirmek için, optimum aralıkları MR damper fabrikalarının üretim kapasitesine dayanmaktadır.
Açıkçası, Eşitlik (28) ile elde edilen optimal parametreler, önerilen yarı aktif kontrol algoritmasının zaman gecikmeli optimal kontrol etkinliğini korur, bu da yapı kontrol sisteminin stokastik uyarımlara maruz kalan dengeli optimal güvenilirliği elde etmesini sağlar.
2. Vaka çalışması
Bir MR damperi için zaman gecikmesi telafisi ile önerilen yarı aktif kontrol yönteminin etkinliğini analiz etmek için, bir MR damperine bağlı düzlemsel tek katlı bir kesme çerçevesi yapısı, Şekil 2'de gösterildiği gibi yatay stokastik sismik yer hareketine tabi tutulmuştur. Yarı aktif kontrollü yapı sisteminin parametreleri aşağıdaki gibidir: yapı kütlesi 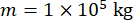 , doğal dairesel frekans
, doğal dairesel frekans 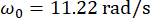 , sönümleme oranı
, sönümleme oranı 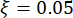 . Geçmiş deneyimlere ve piyasadaki mevcut damper kantarlarına göre, yapısal yer değiştirme, hız, ivme ve kontrol kuvveti eşik değerleri sırasıyla 10 mm, 100 mm/s, 1.500 mm/s2 ve 150 kN'dir. Stokastik sismik yer hareketini temsil etmek için, fiziksel olarak motive edilmiş stokastik yer hareketi modeli kullanılmıştır43:
. Geçmiş deneyimlere ve piyasadaki mevcut damper kantarlarına göre, yapısal yer değiştirme, hız, ivme ve kontrol kuvveti eşik değerleri sırasıyla 10 mm, 100 mm/s, 1.500 mm/s2 ve 150 kN'dir. Stokastik sismik yer hareketini temsil etmek için, fiziksel olarak motive edilmiş stokastik yer hareketi modeli kullanılmıştır43:
 (29) buyurmuştur.
(29) buyurmuştur.
Nerede 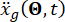 , mühendislik sahasındaki zaman alanındaki yer hareketini temsil eder ve
, mühendislik sahasındaki zaman alanındaki yer hareketini temsil eder ve 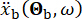 ana kayadaki frekans alanındaki yer hareketini belirtir. Vektör
ana kayadaki frekans alanındaki yer hareketini belirtir. Vektör 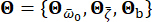 , mühendislik sahasının yüzeyindeki yer hareketinin stokastik doğasını karakterize eder. Parametreler
, mühendislik sahasının yüzeyindeki yer hareketinin stokastik doğasını karakterize eder. Parametreler 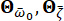 , baskın frekans
, baskın frekans 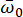 ve eşdeğer sönümleme
ve eşdeğer sönümleme 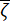 dahil olmak üzere saha toprağının özelliklerini tanımlayan stokastik değişkenlerdir. Vektör
dahil olmak üzere saha toprağının özelliklerini tanımlayan stokastik değişkenlerdir. Vektör 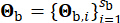 , kaynak özelliklerinden ve yayılma yolundan
, kaynak özelliklerinden ve yayılma yolundan 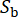 etkilenen ana kayadaki yer hareketinin stokastik doğasını temsil eder ve bu aşamada yer alan stokastik değişkenlerin sayısını gösterir.
etkilenen ana kayadaki yer hareketinin stokastik doğasını temsil eder ve bu aşamada yer alan stokastik değişkenlerin sayısını gösterir. 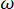 dairesel frekansı ifade eder ve i hayali birimdir.
dairesel frekansı ifade eder ve i hayali birimdir.
Mühendislik sahasının baskın frekansı  ve eşdeğer sönümleme oranı
ve eşdeğer sönümleme oranı 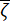 , saha toprağının dinamik özelliklerini karakterize eden temel parametrelerdir. Bu büyüklüklerin olasılık dağılımı ve istatistiksel parametreleri, belirli bir mühendislik alanı sınıfından toplanan sismik ivme kayıtlarına dayalı olarak belirlenebilir. Açıklama amacıyla, [150, 250] m/s kesme dalgası hız aralığına sahip bir saha sınıfı düşünülmüş ve yer hareketinin tasarım karakteristik periyodu 0,45 s olarak ayarlanmıştır.
, saha toprağının dinamik özelliklerini karakterize eden temel parametrelerdir. Bu büyüklüklerin olasılık dağılımı ve istatistiksel parametreleri, belirli bir mühendislik alanı sınıfından toplanan sismik ivme kayıtlarına dayalı olarak belirlenebilir. Açıklama amacıyla, [150, 250] m/s kesme dalgası hız aralığına sahip bir saha sınıfı düşünülmüş ve yer hareketinin tasarım karakteristik periyodu 0,45 s olarak ayarlanmıştır.
Kritik parametreler ,
, 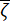 her ikisi de parametre tanımlaması için log-normal bir dağılımı takip eden karşılıklı bağımsız stokastik değişkenler olarak ele alındı. İstatistiksel parametreler aşağıdaki gibidir: 'nin
her ikisi de parametre tanımlaması için log-normal bir dağılımı takip eden karşılıklı bağımsız stokastik değişkenler olarak ele alındı. İstatistiksel parametreler aşağıdaki gibidir: 'nin 
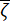 ortalaması sırasıyla 12 rad/s ve 0.1 idi. ve varyasyon
ortalaması sırasıyla 12 rad/s ve 0.1 idi. ve varyasyon 
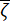 katsayıları sırasıyla 0.42 ve 0.35 idi. Ana kayadaki yer hareketi, 0.20 g'lık bir tepe yer ivmesine karşılık gelen 2 m/s2'lik bir Fourier genliğine sahip bir Gauss beyaz gürültü süreci olarak modellenmiştir. Ana kaya hareketini oluşturmak için kullanılan faz açısı şu şekilde
katsayıları sırasıyla 0.42 ve 0.35 idi. Ana kayadaki yer hareketi, 0.20 g'lık bir tepe yer ivmesine karşılık gelen 2 m/s2'lik bir Fourier genliğine sahip bir Gauss beyaz gürültü süreci olarak modellenmiştir. Ana kaya hareketini oluşturmak için kullanılan faz açısı şu şekilde 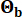 gösterildi: . Bu nedenle, Sb =1 ve
gösterildi: . Bu nedenle, Sb =1 ve 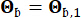 . Bu yaklaşım, belirli bir aşma olasılığı44 ile koşullu stokastik yer hareketlerinin modellenmesi olarak düşünülebilir. Log-normal dağılım varsayımı, gözlemlenen yer hareketi parametrelerinin çarpık doğasını yakalama kabiliyeti nedeniyle yer hareketi modellemesinde yaygın olarak kullanılmaktadır.
. Bu yaklaşım, belirli bir aşma olasılığı44 ile koşullu stokastik yer hareketlerinin modellenmesi olarak düşünülebilir. Log-normal dağılım varsayımı, gözlemlenen yer hareketi parametrelerinin çarpık doğasını yakalama kabiliyeti nedeniyle yer hareketi modellemesinde yaygın olarak kullanılmaktadır.
Bu varsayımın duyarlılığını değerlendirmek için, normal ve gama dağılımları da dahil olmak üzere alternatif olasılık dağılımları kullanılarak ek analizler yapılmıştır45,46. Bulgular, genel eğilimler tutarlı kalırken, log-normal dağılımın, özellikle yer hareketi yoğunluğu ölçümlerinin kuyruk davranışını yakalamak için gözlemlenen verilere en iyi uyumu sağladığını göstermektedir
Teğet küreler yöntemi47 sayesinde, ilişkili atanmış olasılıklara sahip 221 temsili noktadan oluşan bir koleksiyon seçildi ve temsili yer ivmeleri sentezlendi. Örnekleme frekansı 50 Hz ve yer hareketlerinin süresi 20.48 s idi. Simüle edilmiş yer hareketine durağan olmayan bir yoğunluk atamak için, düzgün bir modülasyon fonksiyonu kullanıldı ve formülasyonu aşağıdaki gibiydi42:
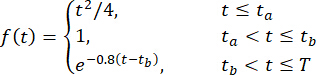 (30) buyurmuştur.
(30) buyurmuştur.
Burada 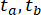 sırasıyla 2 ve 16 s alın.
sırasıyla 2 ve 16 s alın.
Stokastik sismik yer hareketinin ortalama ve standart sapması ve temsili sismik yer hareketinin zaman geçmişi Şekil 3'te gösterilmektedir. Ortalamanın genliği (0.06 m/s2), standart sapmanın (0.8 m/s2) genliğinin ~%8'i idi, bu da fiziksel olarak motive edilmiş stokastik yer hareketi modelinin sıfır ortalama özelliğini sergilediğini gösteriyor. Bu arada, sismik yer hareketi hem zamansal hem de frekans alanlarında dikkate değer durağan olmayan davranışlar sergiledi.
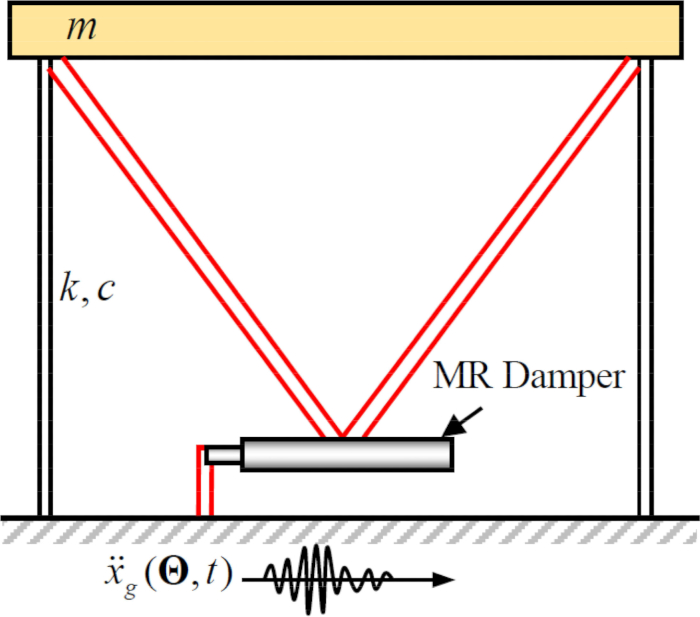
Şekil 2: Manyetolojik sönümleyicili tek katlı bir kesme çerçevesinin çizimi.  yapı kütlesini, sönümleme oranını ve sertliği belirtir;
yapı kütlesini, sönümleme oranını ve sertliği belirtir; 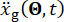 stokastik sismik uyarımı belirtir. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
stokastik sismik uyarımı belirtir. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
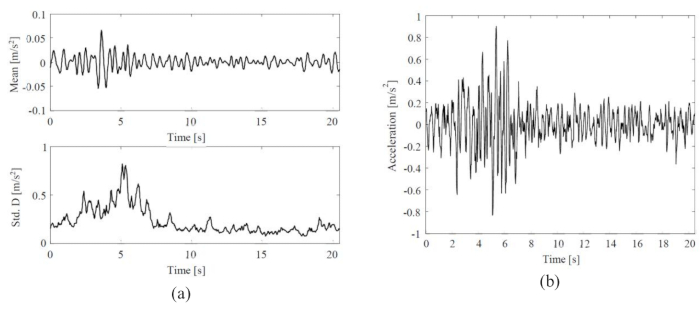
Şekil 3: Seçilen sismik yer hareketlerinin istatistikleri ve temsili örnekleri. (A) Stokastik sismik yer hareketinin ortalama ve standart sapması; (B) Temsili sismik yer hareketinin zaman geçmişi. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
2.1 Zaman gecikmesinin etki analizi
Zaman gecikmesinin bir MR damperinin yarı aktif kontrol etkinliği üzerindeki etkisini analiz etmek için, Şekil 4 , kontrol edilen yapının yer değiştirmesini, hızını ve ivme RMS'sini (kök-ortalama-kare yanıtı) göstermektedir. Ağırlıklandırma matrisi oranı ve damper parametreleri 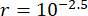 , zaman gecikmesi olmadan optimize edilmiş sonuçlar olan ,
, zaman gecikmesi olmadan optimize edilmiş sonuçlar olan , 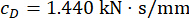 , ve
, ve 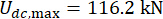 idi38. Kontrol edilen yapının zaman gecikmeli tepkileri, zaman gecikmeli olmayan kontrollü yapıdan daha büyüktü ve zaman gecikmesinin kontrol etkisi üzerindeki etkisi, zaman gecikmesinin artmasıyla birlikte periyodikliği temsil ediyordu. MR sönümleyici ile yarı aktif kontrol yöntemi bir tür geri besleme yöntemi olduğundan, etkinin periyodikliğinin kontrol edilen yapının doğal periyodu (T = 0.56 s) ile ilişkili olduğu düşünülmüştür.
idi38. Kontrol edilen yapının zaman gecikmeli tepkileri, zaman gecikmeli olmayan kontrollü yapıdan daha büyüktü ve zaman gecikmesinin kontrol etkisi üzerindeki etkisi, zaman gecikmesinin artmasıyla birlikte periyodikliği temsil ediyordu. MR sönümleyici ile yarı aktif kontrol yöntemi bir tür geri besleme yöntemi olduğundan, etkinin periyodikliğinin kontrol edilen yapının doğal periyodu (T = 0.56 s) ile ilişkili olduğu düşünülmüştür.
Maksimum MRS yer değiştirmesi, hızı ve ivmesi 24.6 mm, 270.0 mm/s ve 3111.3 mm/s2 olan kontrolsüz yapının tepkileri ile karşılaştırıldığında, MR sönümleyici kontrollü yapı kayda değer bir etki elde etti. Zaman gecikmesi25 ile aktif kontrollü yapının kararsızlığının aksine, MR damper tabanlı yarı aktif kontrol yöntemi, zaman gecikmeli olsa bile hala bir miktar etki elde etti.

Şekil 4: Kontrol edilen yapının zamanla verdiği yanıtların maksimum kök-ortalama-kareleri. (A) Yer değiştirme; (b) hız; (C) Hızlanma. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Zaman gecikmesinin yarı aktif olarak kontrol edilen bir yapının güvenilirliği üzerindeki etkisini analiz etmek için, Şekil 5 , artan zaman gecikmesi ile yer değiştirme, hız ve ivmenin güvenilirliğini göstermektedir. Herhangi bir zaman gecikmesi ile kontrol edilen yapı yanıtlarının güvenilirliği, zaman gecikmesi olmayan değerlere göre daha düşüktü, bu da kontrol edilen yapının güvenilirliğinin zaman gecikmesi ile azaldığı anlamına geliyor. Bu arada, maksimum RMS'ye benzer şekilde, güvenilirlik kontrol etkisi, artan zaman gecikmesi ile periyodiklik gösterdi. Ayrıca, zaman gecikmeli veya gecikmesiz kontrollü yapının güvenilirliği, yer değiştirme, hız ve ivme güvenilirliği 0.0954, 0.1058 ve 0.1111 olan kontrolsüz yapıların değerlerinden daha yüksekti.
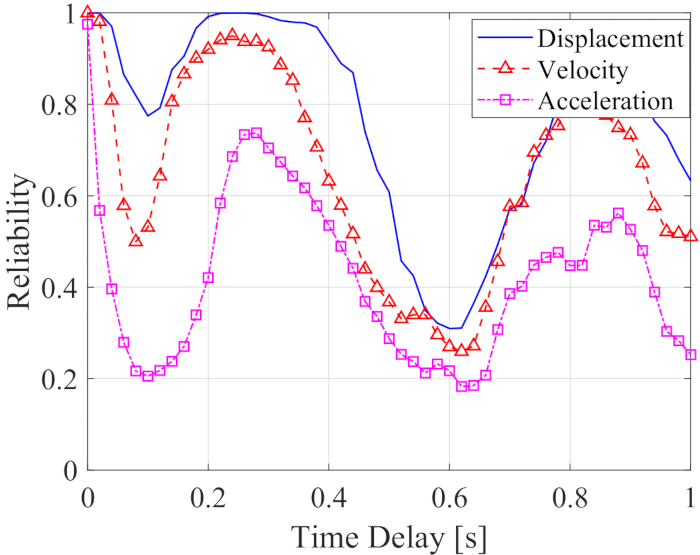
Şekil 5: Artan zaman gecikmesi ile kontrollü yapının yanıtlarının güvenilirliği. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Özetle, yapının tepkileri yarı aktif kontrol yöntemi ile hafifletilmiştir. Bununla birlikte, RMS veya güvenilirliğinden bağımsız olarak, yarı aktif kontrol yönteminin kontrol etkinliği, zaman gecikmesi ile azalmıştır. Bu nedenle, zaman gecikmesini telafi etmek gerekir.
2.1.1 Zaman gecikmesi kompanzasyon yönteminin analizi
Önerilen zaman gecikmesi kompanzasyon yönteminin etkinliğini analiz etmek için, kontrolsüz (Unc) için yer değiştirme, hız ve ivmenin RMS zaman geçmişleri, kompanzasyon kontrollü olmayan zaman gecikmeli sistem (TDN-SAC-PSO) ve kompanzasyon kontrollü zaman gecikmeli sistem (TDC-SAC-PSO) zaman gecikmesinin 0,1 s olduğu Şekil 6'da karşılaştırılmıştır. Ağırlıklandırma matrisinin ve yarı aktif kontrol yönteminin parametreleri, adım 2.1'deki ile aynıdır.

Şekil 6: Farklı yöntemlerle kontrol edilen yapıların kök-ortalama-kare zaman geçmişi karşılaştırması. (A) Yer değiştirme; (b) hız; (c) hızlanma; (D) Kontrol kuvveti. Kısaltmalar: Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; TDN -SAC-PSO = kompanzasyon kontrolsüz zaman gecikmeli sistem. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Her iki kontrol yöntemi de kontrolsüz yapıya kıyasla yapının tepkilerini önemli ölçüde azaltmış ve MR damper tabanlı kontrol yönteminin avantajlarını ortaya koymuştur. Kontrolsüz yapı ile karşılaştırıldığında, TDN-SAC-PSO yöntemi ile maksimum yer değiştirme, hız ve ivme RMS'si %75.79, %73.75 ve %61.22 oranında azaltılır. Ayrıca zaman gecikmesi kompanzasyonu ile kontrol edilen yapının tepkileri TDC-SAC-PSO yöntemi ile %82.59, %80.40 ve %73.04 oranında azaltılmıştır. TDC-SAC-PSO yöntemi ile kontrol kuvvetinin maksimum RMS'si, TDN-SAC-PSO yöntemine kıyasla %8,43 oranında azalmıştır, ancak eski yöntemin titreşim tepkileri ikincisine göre daha azdır. Yukarıdaki analiz, MR damper tabanlı kontrol yöntemi üzerindeki zaman gecikmesinin etkisinin, MR damper yarı aktif kontrol yöntemi için zaman gecikmesi kompanzasyonunun gerekliliğini gösteren kompanzasyon yöntemi ile etkili bir şekilde azaltıldığını göstermektedir.

Şekil 7: Yapı yanıtlarının tipik zamanlarında PDF karşılaştırması. (A) Yer değiştirme; (b) hız; (C) Hızlanma. Kısaltmalar: PDF = olasılık yoğunluk fonksiyonu; Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; TDN -SAC-PSO = kompanzasyon kontrolsüz zaman gecikmeli sistem. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Önerilen kompanzasyon yönteminin kontrol edilen yapının tepkilerinin belirsizliği üzerindeki etkisini kapsamlı bir şekilde ortaya çıkarmak için, tipik zamanlarda, 3, 7 ve 11s'de yer değiştirme, hız ve ivmenin olasılık yoğunluk fonksiyonu (PDF) karşılaştırmaları Şekil 7'de gösterilmektedir. TDN-SAC-PSO yöntemi için PDF'ler Kontrolsüz yapınınkinden daha dardı, bu da yapı yanıtlarının belirsizliğinin zaman gecikmeli olsa bile yarı aktif kontrol yöntemi ile azaldığı anlamına geliyor. Zaman gecikmesi telafi edildiğinde, yanıtların PDF'leri daha da daraltıldı. Bu nedenle, önerilen kompanzasyon yöntemi, yarı aktif kontrol etkisinin iyileştirilmesi için gereklidir.
| Kontrol metodu | Yer değiştirme | Hız | İvme | Kontrol Kuvveti | Minimum değer |
| UNC | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
Tablo 1: Farklı yöntemlerle kontrol edilen yapıların titreşim tepkileri ve kontrol kuvveti güvenilirliği. Kısaltmalar: Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; TDN -SAC-PSO = kompanzasyon kontrolsüz zaman gecikmeli sistem.
Kontrolsüz, TDC-SAC-PSO- ve TDN-SAC-PSO yöntemi ile kontrol edilen yapıların titreşim tepkileri ve kontrol kuvveti güvenilirliği Tablo 1'de gösterilmektedir. TDN-SAC-PSO yöntem kontrolü ile, yapının güvenilirliği, MR damper tabanlı kontrol yönteminin etkinliğini zamanla bile doğrulayan Kontrolsüz yapıya kıyasla önemli ölçüde artırıldı. Bununla birlikte, zaman gecikmesi telafisi ile, özellikle hızlanma için, tazminatsıza kıyasla güvenilirlik önemli ölçüde artırıldı. TDC-SAC-PSO yöntemi için farklı yanıtların güvenilirliği ve kontrol kuvvetinin önemli farklılıklar göstermesi de dikkat çekicidir. Bu, zaman gecikmeli kontrol için kritik parametrelerin optimal değerlerinin, zaman gecikmeli kontrol için optimal olmadığını gösterir. Titreşim tepkilerinin ve zaman gecikmesi etkisi ile kontrol kuvvetinin optimum kontrol etkisini elde etmek için parametrelerin daha da optimize edilmesi gerekir. Yukarıdaki analize dayanarak, bir MR damperi ile yarı aktif kontrol yönteminin yapının titreşim tepkilerini etkili bir şekilde azaltabileceği, zaman gecikmesinin etkisi nedeniyle parametrelerin optimize edilmesi gerektiği sonucuna varılmıştır.
2.2 Parametre optimizasyonu
Parametrelerin optimal değerlerini elde etmek için, güvenilirlik kriterine dayalı entegre optimizasyon yöntemi uygulanmıştır38. Kritik parametrelerin optimizasyonu , 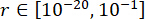 ,
, 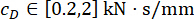
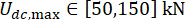 , ve MR damper kuvvetinin ayarlanabilir süreleri s = 8 ile
, ve MR damper kuvvetinin ayarlanabilir süreleri s = 8 ile  gerçekleştirilmiştir. Optimizasyonu uygulamak için MATLAB içindeki GA araç kutusu kullanıldı.
gerçekleştirilmiştir. Optimizasyonu uygulamak için MATLAB içindeki GA araç kutusu kullanıldı.
Parametrelerin 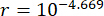 optimizasyon sonuçları ,
optimizasyon sonuçları , 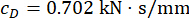 , ve
, ve  zaman gecikmesi
zaman gecikmesi  içindir. Şekil 8 , Kontrolsüz (Unc), TDC-SAC-PSO yöntemi ve SOSC-PSO yöntemi kontrollü yapılar için yer değiştirme, hız, ivme ve kontrol kuvvetinin RMS zaman geçmişlerini göstermektedir. SOSC-PSO yöntemi, zaman gecikmesi telafisi ve optimize edilmiş kritik parametre değerleri ile yarı aktif kontrol yöntemini ifade eder.
içindir. Şekil 8 , Kontrolsüz (Unc), TDC-SAC-PSO yöntemi ve SOSC-PSO yöntemi kontrollü yapılar için yer değiştirme, hız, ivme ve kontrol kuvvetinin RMS zaman geçmişlerini göstermektedir. SOSC-PSO yöntemi, zaman gecikmesi telafisi ve optimize edilmiş kritik parametre değerleri ile yarı aktif kontrol yöntemini ifade eder.

Şekil 8: Kontrolsüz ve TDC-SAC-PSO yöntemi ve SOSC-PSO yöntemi kontrollü yapılar için yer değiştirme, hız, ivme ve kontrol kuvvetinin RMS zaman geçmişleri. (A) Yer değiştirme; (b) hız; (c) hızlanma; (D) Kontrol kuvveti. Kısaltmalar: Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; SOSC-PSO = Zaman gecikmesi telafisi ile Stokastik Optimal Yarı aktif Kontrol yöntemi. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Şekil 8'den, TDC-SAC-PSO ve SOSC-PSO yöntemlerinin kontrol etkilerinin çok az fark gösterdiği görülmektedir. İlk yöntem için yer değiştirme hızı ve ivmesinin maksimum RMS'si, kontrolsüz yapının %81.60, %81.21, %73.62'si ve ikinci yöntem için %82.59, %80.40, %73.04 idi. Her iki kontrol yöntemi için yanıtların olasılık özelliklerini kapsamlı bir şekilde analiz etmek için, Şekil 9, Kontrolsüz, TDC-SAC-PSO yöntemi ve SOSC-PSO yöntemi kontrollü yapılar için yer değiştirme, hız ve ivme PDF'lerini göstermektedir. Her iki kontrol yöntemi de tipik zamanlarda neredeyse aynı yer değiştirme ve hız PDF'lerine sahipti. SOSC-PSO yönteminin ivme PDF'leri, TDC-SAC-PSO yöntemininkinden daha dardı, bu da ivme belirsizliğinin önceki yöntemle daha iyi bir kontrol etkisi elde ettiği anlamına geliyor.
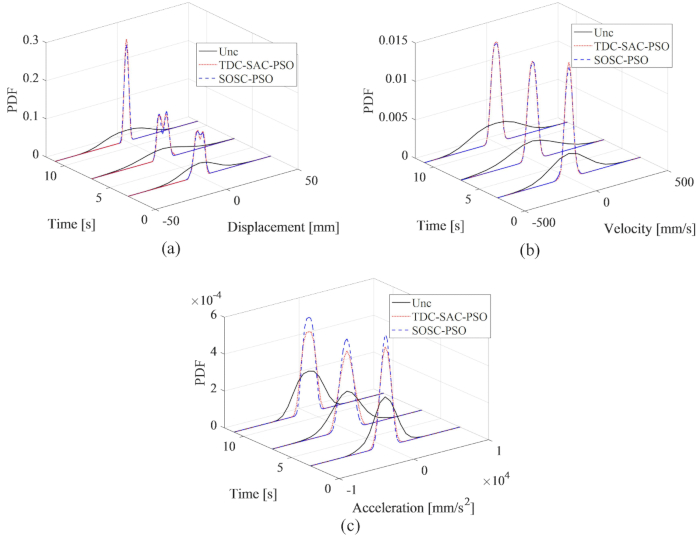
Şekil 9: Farklı kontrollü yapılar için yer değiştirme, hız ve ivmenin PDF'leri karşılaştırması. (A) Yer değiştirme; (b) hız; (C) Hızlanma. Kısaltmalar: PDF'ler = olasılık yoğunluk fonksiyonları; Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; SOSC-PSO = Zaman gecikmesi telafisi ile Stokastik Optimal Yarı aktif Kontrol yöntemi. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Kontrolsüz ve TDC-SAC-PSO- ve SOSC-PSO yöntemi kontrollü yapılar için yer değiştirme, hız, ivme ve kontrol kuvvetinin güvenilirliği Tablo 2'de gösterilmektedir. Her iki kontrol yöntemi de kontrolsüz yapıya kıyasla güvenilirlikte önemli bir artış sağlamıştır. Deplasman güvenilirliği TDC-SAC-PSO ve SOSC-PSO yöntemleri arasında çok az fark gösterdi. Kontrollü yapının en düşük güvenilirliği olan ivme güvenilirliği ise gözle görülür bir artış elde etti. Bu, SOSC-PSO yönteminin dengenin optimal kontrol etkisini sağladığı anlamına gelir.
| Kontrol metodu | Yer değiştirme | Hız | İvme | Kontrol kuvveti | Minimum değer |
| UNC | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
Tablo 2: Farklı yöntemlerle kontrol edilen yapılar için güvenilirlik. Kısaltmalar: Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; SOSC-PSO = Zaman gecikmesi telafisi ile Stokastik Optimal Yarı aktif Kontrol yöntemi.
Önerilen SOSC-PSO yönteminin zaman gecikmeli  etkinliği analiz edildi. Farklı zaman gecikmeleri için önerilen yöntemi daha fazla doğrulamak için, Tablo 3 , zaman gecikmesi aralığı
etkinliği analiz edildi. Farklı zaman gecikmeleri için önerilen yöntemi daha fazla doğrulamak için, Tablo 3 , zaman gecikmesi aralığı  için en uygun parametre değerlerini ve karşılık gelen güvenilirliği göstermektedir.
için en uygun parametre değerlerini ve karşılık gelen güvenilirliği göstermektedir.
| tD(ler) | lg(r*) | CD (kN·s / mm) | Udc,maks (kN) | Yer değiştirme | Hız | İvme | Kontrol kuvveti |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| UNC | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
Tablo 3: Farklı zaman gecikmeleri için optimum parametre değerleri ve karşılık gelen güvenilirlik değerleri. 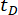 zaman gecikmesini belirtir;
zaman gecikmesini belirtir; 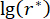 r'nin optimal Logaritmik değerini belirtir, r, kontrol ağırlıklandırma matrisinin katsayısını gösterir;
r'nin optimal Logaritmik değerini belirtir, r, kontrol ağırlıklandırma matrisinin katsayısını gösterir; 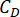 MR damperinin viskoz sönümleme katsayısını gösterir;
MR damperinin viskoz sönümleme katsayısını gösterir; 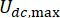 MR damperinin maksimum ve minimum Coulombic kuvvetlerini gösterir.
MR damperinin maksimum ve minimum Coulombic kuvvetlerini gösterir.
Yer değiştirme, hız ve ivmenin güvenilirliğinin, zaman gecikmesinin varlığında bile, kontrolsüz yapıya kıyasla iyileştirildiği gözlemlenebilir ve bu da önerilen yöntemin bu tür gecikmelere karşı sağlamlığını göstermektedir. Bununla birlikte, önerilen kontrol yöntemi ile yapısal tepkilerin güvenilirliği, zaman gecikmesi arttıkça azalmıştır, bu da zaman gecikmesinin kontrol etkinliği üzerindeki etkisinin hafifletilebildiğini, ancak tamamen ortadan kaldırılamayacağını göstermektedir. Özellikle, kontrol kuvvetinin güvenilirliği, farklı zaman gecikmelerinde %90'ın üzerinde kaldı.
3. Sayısal örnek
MDOF yapısında önerilen SOSC-PSO yöntemini doğrulamak için, Şekil 10'da gösterildiği gibi, birinci ve üçüncü katlara monte edilmiş iki MR damperli altı katlı bir yapı analiz edildi. Bölüm 2'de stokastik sismik model ile üretilen sismik numuneler uygulanmış ve yer değiştirme, hız, ivme ve kontrol kuvvetinin güvenilirlik eşikleri 20 mm, 200 mm/s, 3.000 mm/s2 ve 200 kN olarak bulunmuştur. Denk. (27) ile ağırlıklandırma matrisi  olarak kullanılmıştır. MATLAB'ın GA araç kutusu, ,
olarak kullanılmıştır. MATLAB'ın GA araç kutusu, ,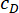 ve , en uygun aralıklarla
ve , en uygun aralıklarla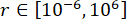 ,
, 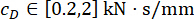 , ve
, ve 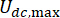
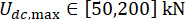 'yi optimize
'yi optimize 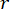 etmek için kullanıldı.
etmek için kullanıldı.

Şekil 10: İki MR damperli altı katlı yapı. Kısaltma: MR = manyetorheolojik. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
3.1 Zaman gecikmesinin etki analizi
Zaman gecikmesinin MDOF yapısındaki MR damperinin kontrol etkinliği üzerindeki etkisini analiz etmek için, Şekil 11, TDC-SAC-PSO yöntemi için zaman gecikmesi ile birlikte yer değiştirme (katlar arası yer değiştirme), hız (katlar arası hız) ve ivmenin (kat ivmesi) maksimum RMS'sini göstermektedir. Parametreler ,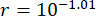
 , ve
, ve 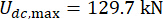 1. kattaki MR damperi için;
1. kattaki MR damperi için;  ve
ve 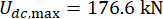 3. kattaki MR damperi için, zaman gecikmesi olmadan optimize edilmiş sonuçlardır. Kontrol edilen yapı yanıtlarının maksimum RMS'si, zaman gecikmesi ile birlikte periyot dalgalanması sergiledi. Maksimum yer değiştirme ve hız RMS'si 1. katta, maksimum ivme 6. kattaydı. Ayrıca, herhangi bir zaman gecikmesi ile verilen yanıtların tüm maksimum MRS'si, zaman gecikmesi olmayan değerlerden daha büyüktü, bu da zaman gecikmesinin MR damperinin kontrol etkisini azalttığı anlamına gelir.
3. kattaki MR damperi için, zaman gecikmesi olmadan optimize edilmiş sonuçlardır. Kontrol edilen yapı yanıtlarının maksimum RMS'si, zaman gecikmesi ile birlikte periyot dalgalanması sergiledi. Maksimum yer değiştirme ve hız RMS'si 1. katta, maksimum ivme 6. kattaydı. Ayrıca, herhangi bir zaman gecikmesi ile verilen yanıtların tüm maksimum MRS'si, zaman gecikmesi olmayan değerlerden daha büyüktü, bu da zaman gecikmesinin MR damperinin kontrol etkisini azalttığı anlamına gelir.

Şekil 11: TDC-SAC-PSO yöntem kontrollü yapı için zaman gecikmesi ile birlikte yanıtların maksimum RMS'si. (A) Yer değiştirme; (b) hız; (C) Hızlanma. Kısaltmalar: RMS = kök-ortalama-kare; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Zaman gecikmesi ile birlikte yer değiştirme, hız ve ivmenin güvenilirliği Şekil 12'de gösterilmektedir. Hız ve ivmenin güvenilirliği, zaman gecikmesi ile birlikte periyot dalgalanması gösterirken, yer değiştirmenin güvenilirliği zaman gecikmesi ile birlikte önemli ölçüde azalmıştır; Herhangi bir zaman gecikmesindeki tüm güvenilirlik değerleri, zaman gecikmesi olmayanlardan daha düşüktü. Bu nedenle, zaman gecikmesinin MR damper kontrollü yapının güvenilirliği üzerindeki etkisini azaltmak için zaman gecikmesi kompanzasyon yöntemi gereklidir.
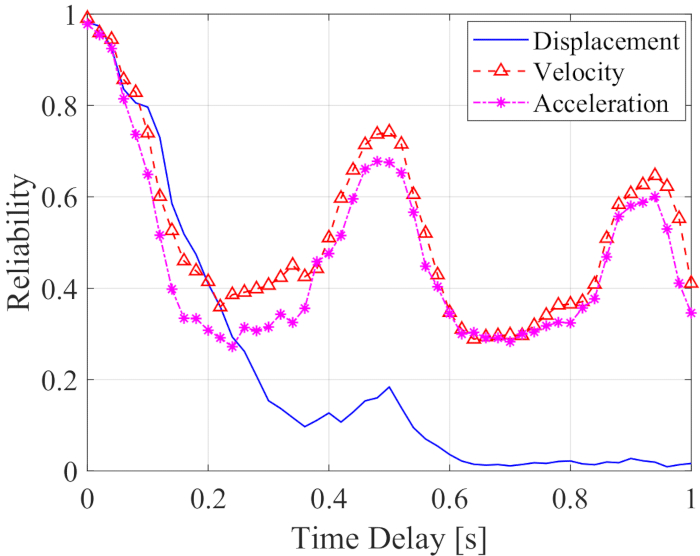
Şekil 12: Zaman gecikmesi ile birlikte kontrollü yapı tepkilerinin güvenilirliği. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
3.2 Zaman gecikmesi telafisinin kontrol etkisi
Önerilen TDC-SAC-PSO yöntemine dayanarak, iki MR sönümleyicili 6-DOF yapısı analiz edildi. Şekil 13, Kontrolsüz (Unc), TDC-SAC-PSO yöntem kontrollü ve TDN-SAC-PSO yöntem kontrollü yapılar için 1. ve 3. katlarda RMS yer değiştirme ve ivmelenme zaman geçmişlerini göstermektedir. Zaman gecikmesi 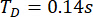 idi ve ağırlıklandırma matrisi oranı
idi ve ağırlıklandırma matrisi oranı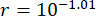 ; MR damper parametreleri 1. kat için idi
; MR damper parametreleri 1. kat için idi
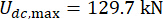 ; ve
; ve 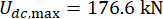 3. kat için.
3. kat için. 

Şekil 13: Farklı yöntemlerle kontrol edilen yapılar için 1. ve 3. katlarda yer değiştirme ve ivmenin RMS zaman geçmişleri. (A) 1. katta yer değiştirme; (B) 3. katta yer değiştirme; (C) 1. katta hızlanma; (D) 3. katta hızlanma. Kısaltmalar: RMS = kök-ortalama-kare; Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; TDN -SAC-PSO = kompanzasyon kontrolsüz zaman gecikmeli sistem. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
1. ve 3. katlardaki maksimum yer değiştirme RMS'si, zaman gecikmesinin telafi edilmediği TDN-SAC-PSO yöntemi ile %35.42 ve %30.44 oranında azaltılmıştır. Tazminat ile birlikte, 1. ve 3. katlardaki maksimum yer değiştirme RMS'si sırasıyla %49,33 ve %53,39 azaltıldı. Tazminat olmadan, 1. ve 3. katlardaki maksimum hızlanma RMS'si %16.22 ve %2.88 arttı, ancak tazminatla birlikte sırasıyla %25.77 ve %36.00 azaldı. Bu nedenle, MR damper kontrol yönteminde zaman gecikmesinin telafisi, özellikle ivmelenme için yapının tepkilerini azaltmak için gereklidir.
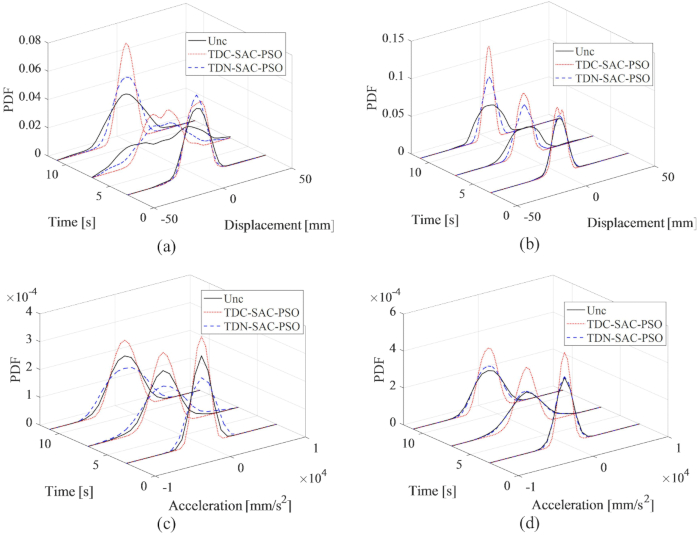
Şekil 14: Farklı kontrol yöntemleri için 1. ve 3. katlarda yer değiştirme ve ivme PDF'leri. (A) 1. katta yer değiştirme; (B) 3. katta yer değiştirme; (C) 1. katta hızlanma; (D) 3. katta hızlanma. Kısaltmalar: PDF'ler = olasılık yoğunluk fonksiyonları; Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; TDN -SAC-PSO = kompanzasyon kontrolsüz zaman gecikmeli sistem. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
1. ve 3. katlardaki yer değiştirme ve ivmelenme PDF'leri Şekil 14'te gösterilmekte olup, TDC-SAC-PSO ve TDN-SAC-PSO yöntemlerinin kontrolsüz yapıya kıyasla farklı kontrol etkilerini ortaya koymaktadır. Tazminat olmadan, 1. ve 3. katlardaki yer değiştirme PDF'leri hala kontrolsüz yapınınkinden daha dardı. Ayrıca, zaman gecikmesinin telafisi ile, yer değiştirme PDF'leri TDN-SAC-PSO yöntem kontrollü yapınınkinden daha dar hale geldi. Yer değiştirmeden farklı olarak, kompanzasyon olmadan, TDN-SAC-PSO yöntemi için 1. kattaki ivme PDF'leri kontrolsüz yapınınkinden daha genişti. Bununla birlikte, telafi ile, hem 1. hem de 3. katlardaki hızlanma PDF'leri, kontrolsüz yapınınkinden daha dardı. Bu nedenle, özellikle hızlanma için yapı tepkilerinin kesinliğini artırmak için zaman gecikmesi telafisinin gerekliliği doğrulanır.
| Kontrol metodu | Yer değiştirme | Hız | İvme | 1. katta kontrol kuvveti | 3. katta kontrol kuvveti |
| UNC | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
Tablo 4: Farklı yöntemlerle kontrol edilen yapılar için güvenilirlik. Kısaltmalar: Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; TDN -SAC-PSO = kompanzasyon kontrolsüz zaman gecikmeli sistem.
Farklı yöntemlerle kontrol edilen yapı sistemleri ile yer değiştirme, hız, ivme ve kontrol kuvvetinin güvenilirlik değerleri Tablo 4'te gösterilmektedir. Yapı yanıtlarının güvenirlik değerleri, eşdeğer uç değer yöntemi25 kullanılarak hesaplanmıştır. TDN-SAC-PSO yöntemi kontrolü ile yer değiştirmenin güvenilirliği kontrolsüz yapıya göre artarken, hız ve ivmenin güvenilirliği azalmıştır. TDC-SAC-PSO yönteminde zaman gecikmesi telafisi ile yer değiştirme, hız ve ivmenin güvenilirliği önemli ölçüde artmıştır. Ayrıca, hem TDN-SAC-PSO hem de TDN-SAC-PSO yöntemleri için kontrol kuvvetinin güvenilirlik değerleri yeterince korunmaktadır. Bu nedenle, önerilen zaman gecikmesi kompanzasyon kontrol yöntemi, MR damper kontrollü yapı için uygun kontrol etkisi sağlar.
3.3 Parametre optimizasyonu
Optimum kontrol etkisini elde etmek için, önerilen kontrol yönteminin parametreleri, güvenilirlik kriterine göre optimize edildi. Zaman gecikmesi 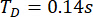 ile en optimal sonuç
ile en optimal sonuç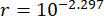 ;
; 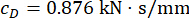 ve
ve  1. kat MR damperi için; ve
1. kat MR damperi için; ve 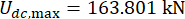 3. MR damperi için.
3. MR damperi için. 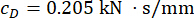
1. ve 3. katlardaki yer değiştirme ve ivmenin RMS zaman geçmişleri, TDC-SAC-PSO ve SOSC-PSO yöntemlerinin ve Kontrolsüz yapının kontrol etkilerinin karşılaştırıldığı Şekil 15'te gösterilmektedir. MR damper kontrolü ile, zaman gecikmesi telafisi olsun ya da olmasın, yer değiştirme ve hızlanma RMS'si önemli ölçüde azaldı. SOSC-PSO yöntemi ile 1. ve 3. katlardaki maksimum yer değiştirme RMS'si, kontrolsüz yapıya göre sırasıyla %65.15 ve %63.16 oranında azalmıştır. TDC-SAC-PSO yöntemi ile karşılaştırıldığında, yer değiştirme tepkisi daha da azaltılmıştır. 1. ve 3. katlardaki maksimum RMS ivmesi, SOSC-PSO yöntemi için %23,39 ve %35,60 oranında azaltılmıştır. SOSC-PSO ve TDC-SAC-PSO yöntemleri için ivmenin kontrol etkisinde çok az fark vardı, bu da zaman gecikmesi telafisinin kontrol etkisinin yer değiştirme ve ivme için farklı olduğunu gösterdi.
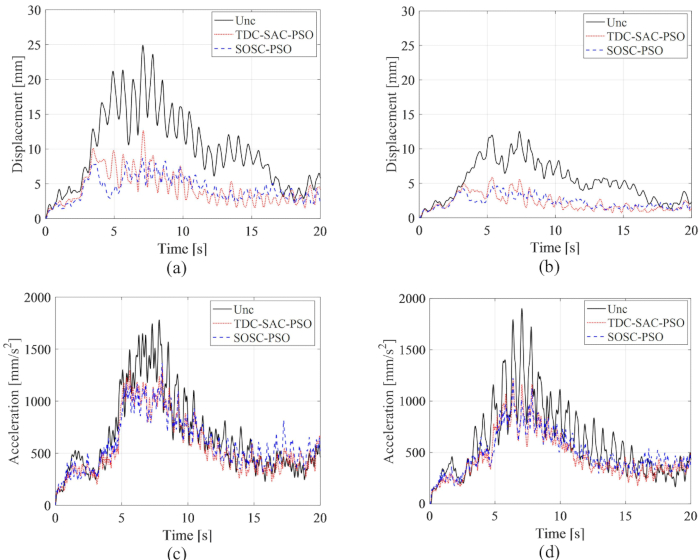
Şekil 15: Farklı kontrol yöntemleri için 1. ve 3. katlarda yer değiştirme ve ivmenin RMS zaman geçmişleri. (A) 1. katta yer değiştirme; (B) 3. katta yer değiştirme; (C) 1. katta hızlanma; (D) 3. katta hızlanma. Kısaltmalar: RMS = kök-ortalama-kare; Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; SOSC-PSO = Zaman gecikmesi telafisi ile Stokastik Optimal Yarı aktif Kontrol yöntemi. Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
1. ve 3. katlardaki yer değiştirme ve ivme PDF'leri Şekil 16'da sunulmuştur; yer değiştirme ve ivme PDF'leri, Kontrolsüz yapı ile karşılaştırıldığında TDC-SAC-PSO ve SOSC-PSO yöntemleriyle daraltıldı. Ayrıca, SOSC-PSO yöntemi için yer değiştirme ve ivme PDF'leri, TDC-SAC-PSO yöntemi kontrollü yapınınkilere kıyasla daha da daraltılmıştır. Bu nedenle, parametre optimizasyonu ile önerilen zaman gecikmesi kompanzasyon kontrol yöntemi, optimizasyon yapılmadığından daha iyi bir kontrol etkisi elde etti.

Şekil 16: Farklı kontrol yöntemleri için 1. ve 3. katlarda yer değiştirme ve ivme PDF'leri. (A) 1. katta yer değiştirme; (B) 3. katta yer değiştirme; (C) 1. katta hızlanma; (D) 3. katta hızlanma. Kısaltmalar: PDF'ler = olasılık yoğunluk fonksiyonları; Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; SOSC-PSO = Zaman gecikmesi telafisi ile Stokastik Optimal Yarı aktif Kontrol yöntemi Bu rakamın daha büyük bir sürümünü görüntülemek için lütfen buraya tıklayın.
Yer değiştirme, hız, ivme ve kontrol kuvvetinin güvenilirlik değerleri Tablo 5'te gösterilmektedir. SOSC-PSO yönteminin güvenirlik değerleri, TDC-SAC-PSO yönteminin güvenirlik değerlerinden daha yüksekti. Bu arada, kontrol kuvveti hala yeterli güvenilirliği korudu. Bu nedenle, MR damper tabanlı kontrol yöntemi için en iyi kontrol etkisini elde etmek için parametrelerin optimizasyonu gereklidir.
| Kontrol metodu | Yer değiştirme | Hız | İvme | 1. katta kontrol kuvveti | 3. katta kontrol kuvveti |
| UNC | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
Tablo 5: Farklı yöntemlerle kontrol edilen yapılar için güvenilirlik. Kısaltmalar: Unc = kontrolsüz; TDC-SAC-PSO = kompanzasyon kontrollü zaman gecikmeli sistem; SOSC-PSO = Zaman gecikmesi telafisi ile Stokastik Optimal Yarı aktif Kontrol yöntemi.
Sonuçlar
Bu yazıda, zaman gecikmesinin MR damper tabanlı yöntemin kontrol etkinliği üzerindeki etkisini amaçlayan, zaman gecikmesi kompanzasyonlu yarı aktif bir kontrol yöntemi önerilmiştir. Önerilen yöntemde, kritik parametreler güvenilirlik kriterine göre optimize edilmiştir. Kontrol etkinliğini karşılaştırarak, aşağıdaki sonuçlar ele alınmaktadır:
(1) Bir MR damperine dayalı yarı aktif kontrol yöntemi, aktif kontrol yönteminden daha sa?...
Tartışmalar
Fiziksel Stokastik Optimal kontrol teorisinin (PSO) tanıtılmasıyla birlikte, bu yazıda, MR damperleri tarafından kontrol edilen yapıların güvenilirliğini korumak için tasarlanmış, zaman gecikmesi kompanzasyonlu bir Stokastik Optimal Yarı Aktif Kontrol yöntemi (SOSC-PSO) önerilmiştir. Önerilen yöntemdeki zaman gecikmesini telafi etmek için, yarı aktif kontrol kuvveti sadece mevcut durumların değil, aynı zamanda ayrık durum uzayında önceki zaman adımlarındaki du...
Açıklamalar
Tüm yazarların beyan edeceği herhangi bir çıkar çatışması yoktur.
Teşekkürler
Yazarlar, Hebei Eyaleti Doğa Bilimleri Vakfı'nın (Hibe No. E2023210007) desteğini minnetle kabul ederler.
Malzemeler
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
Referanslar
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Yeniden Basımlar ve İzinler
Bu JoVE makalesinin metnini veya resimlerini yeniden kullanma izni talebi
Izin talebiThis article has been published
Video Coming Soon
JoVE Hakkında
Telif Hakkı © 2020 MyJove Corporation. Tüm hakları saklıdır