A subscription to JoVE is required to view this content. Sign in or start your free trial.
Research Article
שיטת בקרה סטוכסטית חצי אקטיבית של מבנה המבוססת על בולמים מגנטורולוגיים בהתחשב בעיכוב זמן
In This Article
Summary
במאמר זה מוצעת שיטת בקרה סטוכסטית אופטימלית למחצה עם פיצוי עיכוב זמן (SOSC-PSO), שנועדה לשמור על אמינות המבנים הנשלטים על ידי בולמי MR.
Abstract
השימוש בבולמים מגנטורולוגיים (MR) במערכות בקרה חצי אקטיביות עומד בפני אתגר מרכזי: עיכוב זמן הנגרם על ידי תהליכי משוב, מה שמפחית את האמינות של מבני הנדסה אזרחית תחת עירורים סטוכסטיים. מאמר זה מציע שיטת בקרה חצי אקטיבית אופטימלית סטוכסטית עם פיצוי עיכוב זמן (SOSC-PSO), הממנפת את תיאוריית הבקרה האופטימלית הסטוכסטית הפיזיקלית (PSO) כדי לטפל בבעיה זו ולשמור על אמינות מבנית. השיטה המוצעת גוזרת את כוח הבקרה החצי אקטיבי כפונקציה של המצב הנוכחי והקודם, ומפצה על עיכובי זמן בתהליך הבקרה. כדי לייעל את יעילות הבקרה, פרמטרים מרכזיים מכוונים על סמך קריטריון אמינות למערכת. ניתוחי אימות על מבנים של דרגת חופש אחת וריבוי דרגות חופש תחת עירורים סייסמיים סטוכסטיים מראים כי עיכובים בזמן פוגעים משמעותית בביצועים של בולמי MR. עם זאת, שיטת SOSC-PSO עם פיצוי עיכוב זמן משפרת משמעותית את יעילות הבקרה, ועם פרמטרים אופטימליים, היא משפרת את האמינות של מערכת הבקרה המבנית מעבר לשיטות ללא אופטימיזציה של פרמטרים.
Introduction
שיפור הביצועים של מבנים הנדסיים מול אירועים קטסטרופליים, כגון רעידות אדמה ורוחות קיצוניות, נותר דאגה עיקרית בקהילת ההנדסה האזרחית. בקרה מבנית, טכניקה יעילה להפחתת רעידות, הוכחה כמשפרת הן את הבטיחות והן את הפונקציונליות של מבנים כאלה 1,2,3. במהלך העשורים האחרונים פותחו שיטות וטכנולוגיות מתקדמות שונות למטרה זו. ניתן לסווג שיטות אלו באופן כללי לארבע קטגוריות על סמך סוג האנרגיה המשמשת להנעת התקני הבקרה: מערכות בקרה אקטיביות, חצי אקטיביות, פסיביות והיברידיות 4,5,6,7.
בבקרה אקטיבית, כוח הבקרה הנדרש מופעל ישירות דרך התקני הבקרה, מה שמצריך כמות משמעותית של אנרגיה 8,9,10. בקרה חצי אקטיבית, לעומת זאת, כוללת התאמת המאפיינים של התקני בקרה (כגון שיכוך או קשיחות) על סמך אותות בקרה, הדורשים הרבה פחות אנרגיה בהשוואה למערכות אקטיביות11. שליטה פסיבית, לעומת זאת, מסתמכת על פיזור אנרגיה ללא כל כניסת אנרגיה חיצונית למערכת 12,13,14. מערכות היברידיות משלבות את התכונות של אסטרטגיות בקרה אקטיביות/חצי אקטיביות ופסיביות כדי להשיג ביצועים יעילים יותר15. מבין גישות אלה, בקרה חצי אקטיבית נחשבת למבטיחה במיוחד בשל האיזון שלה בין צריכת אנרגיה נמוכה ויעילות גבוהה 16,17,18. הבולם המגנטורולוגי (MR), עם מאפייני השיכוך הדינמיים המעולים שלו, נחשב לאחד ממכשירי הבקרה החצי אקטיביים היעילים ביותר 19,20,21,22.
עם זאת, מתעורר אתגר במערכות בקרה חצי אקטיביות המשתמשות בבולמי MR, שכן לוגיקת משוב מציגה בהכרח עיכובים בזמן. עיכובים אלו נגרמים בדרך כלל ממספר גורמים 23,24,25, כולל: (i) רכישה ועיבוד של נתוני חיישנים, (ii) חישוב כוח הבקרה הנדרש על ידי הבקר 26, (iii) העברת אותות דרך מתמרים לבולמי MR27, ו-(iv) יצירת הכוח בפועל על ידי בולמי ה-MR עצמם28. עיכובי זמן כאלה יכולים להוביל לפערים בין כוח הבקרה המיוצר לבין הכוח הצפוי על ידי המבנה, מה שפוגע משמעותית ביעילות הבקרה29. למרבה הצער, רוב אלגוריתמי הבקרה הקיימים עבור בולמי MR אינם מביאים בחשבון את העיכובים הללו.
בנוסף, בשל האקראיות המובנית של אירועים קטסטרופליים, כל אלגוריתם בקרה פעיל למחצה יעיל חייב להיות מסוגל לשמור על ביצועים תחת עירורים סטוכסטיים. שיטת הבקרה הגאוסית הריבועית הליניארית (LQG), טכניקת אופטימיזציה סטוכסטית קלאסית, נחקרה להפחתת רעידות במבנים המצוידים בבולמי MR. לדוגמה, Dyke et al. הציעו אסטרטגיית בקרה אופטימלית חתוכה LQG לשיפור התגובה הסייסמית של מבנים המצוידים בבולמי MR, תוך שימוש במשוב תאוצה30. יינג ועמיתיו הציגו אסטרטגיית בקרה אופטימלית סטוכסטית חצי אקטיבית לא חתוכה למבנים לא ליניאריים עם בולמי MR, המשלבת מיצוע סטוכסטי וטכניקות תכנות דינמיות31. מחקרים אחרים יישמו בקרת LQG מבוססת מודאלית כדי לשפר את הביצועים הסייסמיים של מבנים מבודדים בבסיס19 וניתחו את יעילותה להפחתת רעידות במגדלי טורבינות רוח32. עם זאת, שיטות LQG קלאסיות, המניחות רעש גאוס לבן, אינן מתאימות היטב למידול האופי הלא-נייח והלא גאוס של עירורים בעולם האמיתי כמו רעידות אדמה או רוחות חזקות. כדי לטפל בכך, פותח הרעיון של בקרה אופטימלית סטוכסטית מבוססת פיזיקה (PSO)33,34, המתגברת על המגבלות של שיטות LQG מסורתיות ומציעה מסגרת מדויקת יותר לטיפול בעירורים סטוכסטיים מגוונים35. מחקרים הראו כי בקרה אופטימלית סטוכסטית חצי אקטיבית מבוססת PSO משפרת משמעותית את הפחתת הרעידות עבור מבנים ליניאריים ולא ליניאריים כאחד הנתונים לכוחות סייסמיים סטוכסטיים36.
לפיכך, יש צורך דחוף בשיטת בקרה חצי אקטיבית חזקה המפצה על עיכובים בזמן, ומשפרת את האמינות של מבנים הנשלטים על ידי בולמי MR25,37. יתר על כן, כדי להבטיח ביצועי בקרה מיטביים תחת עירורים סטוכסטיים, חיוני לייעל את הפרמטרים הקריטיים של שיטת הבקרה המוצעת באמצעות גישה מבוססת אמינות. לכן, מוצעת במאמר זה שיטת בקרה סטוכסטית אופטימלית למחצה עם פיצוי עיכוב זמן (SOSC-PSO) כדי לשפר את האמינות של מבנים עם בולמי MR.
Protocol
1. שיטת בקרה חצי אקטיבית אופטימלית סטוכסטית
מכיוון שהשפעת הבקרה של בולם MR מושפעת באופן משמעותי מעיכוב הזמן הבלתי נמנע, פותחה שיטת בקרה חצי אקטיבית עם אלגוריתם פיצוי עיכוב זמן כדי להגביר את ביצועי המבנה המבוקר. חוץ מזה, האקראיות הטבועה בעירורים חיצוניים גורמת לאי הוודאות הברורה של תגובות דינמיות. בקרת ה-PSO מוצגת כדי לייעל את הפרמטרים הקריטיים של השיטה המוצעת להבטחת האמינות של מערכת בקרת המבנה.
1.1 אלגוריתם פיצוי של בקרה חצי אקטיבית
מבלי לאבד את הכלליות, שקול מבנה n-Degree-Of-Freedoms (n-DOF) הנשלט על ידי בולמי MR עם עיכוב זמן, שמתוכם משוואת התנועה הנתונה לעירורים סטוכסטיים ניתנת על ידי:
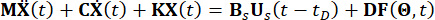 (1)
(1)
כאשר  מייצגים את מטריצות המסה, השיכוך והקשיחות של המבנה, בהתאמה; n מייצג את מספר דרגות החופש של המבנה המבוקר. וקטורי התזוזה, המהירות והתאוצה של המבנה מיוצגים על ידי
מייצגים את מטריצות המסה, השיכוך והקשיחות של המבנה, בהתאמה; n מייצג את מספר דרגות החופש של המבנה המבוקר. וקטורי התזוזה, המהירות והתאוצה של המבנה מיוצגים על ידי 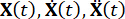 , בהתאמה. הנקודות הקטנות ושתי הנקודות מעל הסמלים מייצגות את הנגזרות של פעם ראשונה ושנייה. Us (t - tD) מייצג את הווקטור הממדי r של כוח הבקרה המושהה בזמן של בולמי MR, ו- r מייצג את מספר הבולמים; t מייצג את הזמן; tD מציין עיכוב זמן, בהנחה שהוא אחיד על פני כל הבולמים במחקר זה, כאשר
, בהתאמה. הנקודות הקטנות ושתי הנקודות מעל הסמלים מייצגות את הנגזרות של פעם ראשונה ושנייה. Us (t - tD) מייצג את הווקטור הממדי r של כוח הבקרה המושהה בזמן של בולמי MR, ו- r מייצג את מספר הבולמים; t מייצג את הזמן; tD מציין עיכוב זמן, בהנחה שהוא אחיד על פני כל הבולמים במחקר זה, כאשר 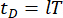 , עם כאן המספר
, עם כאן המספר  האינטגרלי , ומציין
האינטגרלי , ומציין  את תקופת הדגימה.
את תקופת הדגימה. 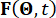 מייצג את וקטור ה-p של עירורים סטוכסטיים, ומייצג
מייצג את וקטור ה-p של עירורים סטוכסטיים, ומייצג  את וקטור הפרמטר הסטוכסטי המאפיין את האקראיות הקשורה לעירורים חיצוניים. הממד של
את וקטור הפרמטר הסטוכסטי המאפיין את האקראיות הקשורה לעירורים חיצוניים. הממד של  תלוי במודל המשמש לעירורים החיצוניים אך אינו קשור לדרגות החופש המכניות של המבנה. Bs ו-D הן מטריצות n x r ו-n x p המציינות את מיקומי הבולמים והעירורים החיצוניים, בהתאמה. בייצוג מרחב המצב, Eq. (1) נכתב כך:
תלוי במודל המשמש לעירורים החיצוניים אך אינו קשור לדרגות החופש המכניות של המבנה. Bs ו-D הן מטריצות n x r ו-n x p המציינות את מיקומי הבולמים והעירורים החיצוניים, בהתאמה. בייצוג מרחב המצב, Eq. (1) נכתב כך:
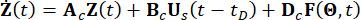 (2)
(2)
כאשר 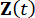 מייצג וקטור מצב דו-ממדי;
מייצג וקטור מצב דו-ממדי; 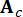 מייצג מטריצת מערכת 2n x 2n;
מייצג מטריצת מערכת 2n x 2n; 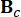 מייצג מטריצת מיקום 2n x r של בולמי MR;
מייצג מטריצת מיקום 2n x r של בולמי MR; 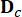 מייצג מטריצת מיקום של 2n x p של עירורים חיצוניים. פרמטרים אלה באים לידי ביטוי כך:
מייצג מטריצת מיקום של 2n x p של עירורים חיצוניים. פרמטרים אלה באים לידי ביטוי כך:
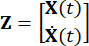 ,
, 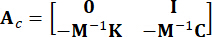 ,
, 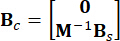 ,
, 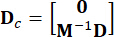 (3)
(3)
כאשר  מציין מטריצת זהות באותו סדר של
מציין מטריצת זהות באותו סדר של 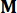 . לנוחיות החישוב, ניתן לבטא את משוואת מרחב המצב הרציף Eq. (2) בצורה בדידה כך:
. לנוחיות החישוב, ניתן לבטא את משוואת מרחב המצב הרציף Eq. (2) בצורה בדידה כך:
 (4)
(4)
כאשר נקודת  הזמן מפושטת כ-
הזמן מפושטת כ- 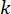 . ו
. ו  - ,
- , 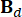 ,
, 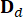 מציין מטריצות 2n x 2n, 2n x r ו- 2n x p, המתבטאות כ:
מציין מטריצות 2n x 2n, 2n x r ו- 2n x p, המתבטאות כ:
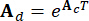 ,
, 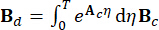 ,
, 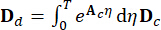 (5)
(5)
כאשר 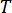 מציין את תקופת הדגימה.
מציין את תקופת הדגימה.
כדי להשיג יעילות דומה לבקרה האקטיבית, מוצעת שיטת בקרה פשוטה ויעילה המבוססת על אלגוריתם Hrovat 38 לבקרה מבוססת בולמי MR עם עיכוב זמן:
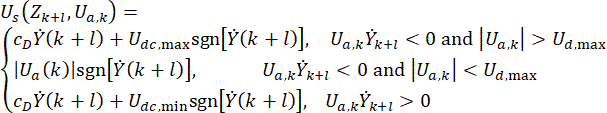 (6)
(6)
כאשר 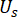 מייצג את אות כוח הבקרה החצי אקטיבי בנקודת הזמן \
מייצג את אות כוח הבקרה החצי אקטיבי בנקודת הזמן \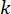 עבור בולם ה-MR;
עבור בולם ה-MR; 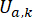 מייצג את כוח הבקרה האקטיבי הייחוס עם פיצוי עיכוב זמן;
מייצג את כוח הבקרה האקטיבי הייחוס עם פיצוי עיכוב זמן;  מייצג את כוח השיכוך המרבי של בולם ה-MR, הניתן לשינוי;
מייצג את כוח השיכוך המרבי של בולם ה-MR, הניתן לשינוי; 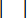 מייצג את סמל פעולת הערך המוחלט;
מייצג את סמל פעולת הערך המוחלט; 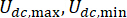 מייצגים את הכוחות הקולומביים המקסימליים והמינימליים של בולם MR;
מייצגים את הכוחות הקולומביים המקסימליים והמינימליים של בולם MR; 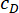 מייצג את מקדם השיכוך הצמיג;
מייצג את מקדם השיכוך הצמיג; 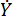 מייצג את כניסת המהירות בבולם MR, שהיא מהירות התנועה של הבוכנה ביחס לצילינדר הבולם. ב-Eq. (6),
מייצג את כניסת המהירות בבולם MR, שהיא מהירות התנועה של הבוכנה ביחס לצילינדר הבולם. ב-Eq. (6), 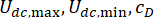 מייצגים את הפרמטרים המתוכננים של בולם ה-MR.
מייצגים את הפרמטרים המתוכננים של בולם ה-MR.
Eq. (6) מציג את חישוב כוח הבקרה החצי אקטיבי של בולם ה-MR עם עיכוב בזמן. נראה כי כוח 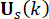 הבקרה החצי אקטיבי , בצעד
הבקרה החצי אקטיבי , בצעד 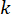 הזמן במשוואה (4), מחושב על סמך כוח
הזמן במשוואה (4), מחושב על סמך כוח  הבקרה הפעיל בצעד
הבקרה הפעיל בצעד 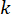 הזמן ומשתנה
הזמן ומשתנה 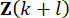 המצב בצעד
המצב בצעד 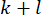 הזמן מאז עיכוב צעדי הזמן
הזמן מאז עיכוב צעדי הזמן 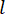 . כדי להשיג את כוח
. כדי להשיג את כוח  הבקרה הפעיל , פונקציית העלות הקונבנציונלית נקבעת על ידי
הבקרה הפעיל , פונקציית העלות הקונבנציונלית נקבעת על ידי
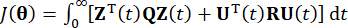 (7)
(7)
כאשר  מייצג את מטריצת השקלול החיובית הסימטרית 2n x 2n של מצב המערכת;
מייצג את מטריצת השקלול החיובית הסימטרית 2n x 2n של מצב המערכת; 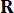 מייצג את מטריצת השקלול החיובית הסימטרית של כוח הבקרה. ניתן לראות כי ההתרגשות החיצונית זניחה. למעשה, בהתבסס על Eq. (7), מערכת בקרת המבנה יכולה להשיג את אפקט הבקרה האופטימלי ללא קשר לסוג העירור החיצוני. כצורה הבדידה, משוואה (7) מבוטאתכ-39:
מייצג את מטריצת השקלול החיובית הסימטרית של כוח הבקרה. ניתן לראות כי ההתרגשות החיצונית זניחה. למעשה, בהתבסס על Eq. (7), מערכת בקרת המבנה יכולה להשיג את אפקט הבקרה האופטימלי ללא קשר לסוג העירור החיצוני. כצורה הבדידה, משוואה (7) מבוטאתכ-39:
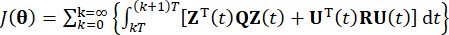 (8)
(8)
המזעור של פונקציית  העלות מוביל לבעיית ערך קיצוני מותנה, וכוח
העלות מוביל לבעיית ערך קיצוני מותנה, וכוח 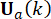 הבקרה האקטיבי מחושב על ידי25:
הבקרה האקטיבי מחושב על ידי25:
 (9)
(9)
כאשר 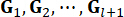 מציין את רווחי הבקרה עבור משתנה
מציין את רווחי הבקרה עבור משתנה 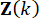 המצב בצעד
המצב בצעד 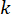 הזמן וכוח
הזמן וכוח 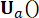 הבקרה הפעיל בצעד
הבקרה הפעיל בצעד  הזמן , אשר נקבע על ידי מטריצות
הזמן , אשר נקבע על ידי מטריצות 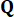 השקלול ו
השקלול ו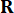 - 37. מאז עיכוב הזמן הבלתי נמנע, כוח
- 37. מאז עיכוב הזמן הבלתי נמנע, כוח  הבקרה המתקבל מופעל על המבנה בנקודות
הבקרה המתקבל מופעל על המבנה בנקודות 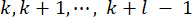 זמן . לכן, כוח הבקרה הפעיל במשוואה (9) מחושב על ידי:
זמן . לכן, כוח הבקרה הפעיל במשוואה (9) מחושב על ידי:
 (10)
(10)
למען בהירות התפיסה, כוח הבקרה הפעיל למחצה ב-Eq. (10) מבוטא באופן הבא בהתבסס על Eq. (6):
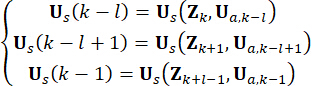 (11)
(11)
כאשר 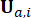 מציין את כוח הבקרה הפעיל בנקודת
מציין את כוח הבקרה הפעיל בנקודת  הזמן . החלפת Eq. (11) ב-Eq. (10),
הזמן . החלפת Eq. (11) ב-Eq. (10),
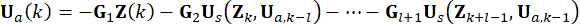 (12)
(12)
הערה: כל ערכי המצב  מנקודת
מנקודת 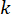 זמן עד
זמן עד 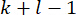 דרושים לחישוב
דרושים לחישוב  . לכן, שיטת חיזוי המצב הבאה מוצגת40.
. לכן, שיטת חיזוי המצב הבאה מוצגת40.
 (13)
(13)
כאשר  מציין את המשתנה החזוי. על ידי האיטרציה של Eq. (13), המצב
מציין את המשתנה החזוי. על ידי האיטרציה של Eq. (13), המצב  ב
ב 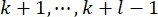 - מחושב. כוח הבקרה הפעיל Ua(k) מתבטא כך:
- מחושב. כוח הבקרה הפעיל Ua(k) מתבטא כך:
 (14)
(14)
ניתן להשיג את כוח הבקרה החצי אקטיבי על ידי שילוב Eqs. (6), (12) ו-(13).
1.2 ניתוח אמינות של מערכת בקרת המבנה
על פי עקרון שימור ההסתברות, המערכת 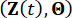 המוגברת והמבנה
המוגברת והמבנה  עם בולמי MR נשמרים בהסתברות, והם נשלטים על ידי משוואות התפתחות צפיפות ההסתברות הכלליות הבאות (GDEEs)38:
עם בולמי MR נשמרים בהסתברות, והם נשלטים על ידי משוואות התפתחות צפיפות ההסתברות הכלליות הבאות (GDEEs)38:
 (15)
(15)
 (16)
(16)
כאשר  ,
, 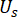 מציין את הרכיבים המתאימים של מצב המערכת וכוח הבקרה הפעיל למחצה עם עיכוב זמן, בהתאמה;
מציין את הרכיבים המתאימים של מצב המערכת וכוח הבקרה הפעיל למחצה עם עיכוב זמן, בהתאמה;  ומציין
ומציין 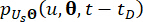 את פונקציות צפיפות ההסתברות המשותפת של מערכות
את פונקציות צפיפות ההסתברות המשותפת של מערכות 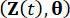 מדגם מוגברות ו- , בהתאמה
מדגם מוגברות ו- , בהתאמה  ;
;  מציין את המדגם בתוך מרחב הדגימה של
מציין את המדגם בתוך מרחב הדגימה של  ;
; 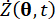 ו
ו 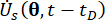 - ) מציין את הנגזרות החלקיות של זמן מסדר ראשון של מצב המערכת ורכיבי כוח בקרה אקטיביים למחצה, בהתאמה. צפיפות ההסתברות המשותפת מתפקדת
- ) מציין את הנגזרות החלקיות של זמן מסדר ראשון של מצב המערכת ורכיבי כוח בקרה אקטיביים למחצה, בהתאמה. צפיפות ההסתברות המשותפת מתפקדת  וניתן
וניתן 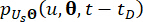 להשיג אותה על ידי פתרון Eqs. (15) ו-(16) בתנאים הראשוניים הבאים:
להשיג אותה על ידי פתרון Eqs. (15) ו-(16) בתנאים הראשוניים הבאים:
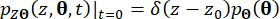 (17)
(17)
 (18)
(18)
כאשר  מציין את פונקציית הדלתא של דיראק;
מציין את פונקציית הדלתא של דיראק; 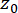 ומציין
ומציין 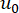 את הערכים ההתחלתיים הדטרמיניסטיים של
את הערכים ההתחלתיים הדטרמיניסטיים של 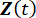 ו
ו 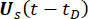 - , בהתאמה;
- , בהתאמה;  מציין את פונקציית צפיפות ההסתברות של המדגם
מציין את פונקציית צפיפות ההסתברות של המדגם 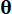 .
.
פונקציות צפיפות ההסתברות המיידיות של 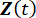 וניתן
וניתן 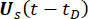 להשיג על ידי אינטגרציה חד-ממדית של
להשיג על ידי אינטגרציה חד-ממדית של  ומעל
ומעל 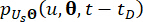 תחום מרחב הדגימה:
תחום מרחב הדגימה:
 (19)
(19)
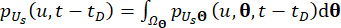 (20)
(20)
כאשר 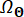 מציין את תחום ההתפלגות של
מציין את תחום ההתפלגות של  .
.
מבוסס על Eqs. (19) ו-(20), ניתן לראות כי המידע ההסתברותי המלא של הכמויות הפיזיקליות הנוגעות בדבר נגזר בקלות, אם מגדירים את הקשרים הקשורים לפרמטרים של אלגוריתם. ניתן לחשב את האמינות של הכמויות הפיזיקליות הנוגעות בדבר על ידי פונקציית הביצועים הרלוונטית הבאה:
 (21)
(21)
 (22)
(22)
כאשר 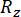 ומציין
ומציין 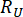 את האמינות המחושבת של כמות המצב הנוגעת בדבר וכוח הבקרה הפעיל למחצה, בהתאמה;
את האמינות המחושבת של כמות המצב הנוגעת בדבר וכוח הבקרה הפעיל למחצה, בהתאמה; 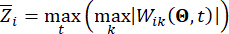 מציין את וקטור הערך הקיצוני המקביל של ה-i-th הנוגע לכמות הפיזית של המבנה המבוקר;
מציין את וקטור הערך הקיצוני המקביל של ה-i-th הנוגע לכמות הפיזית של המבנה המבוקר; 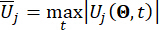 מציין את וקטור הערך הקיצוני המקביל של כוח הבקרה j-th; הכובע '-' על סמלים מציין את וקטור הערך הקיצוני המקביל41;
מציין את וקטור הערך הקיצוני המקביל של כוח הבקרה j-th; הכובע '-' על סמלים מציין את וקטור הערך הקיצוני המקביל41; 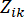 מציין את ה-i-th הנוגע לכמות הפיזית של ה-k-th DOF של המבנה המבוקר;
מציין את ה-i-th הנוגע לכמות הפיזית של ה-k-th DOF של המבנה המבוקר; 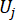 מציין את כוח הבקרה J-th;
מציין את כוח הבקרה J-th;  ,
, 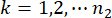 ,
, 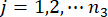 ,
,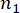 ,
, 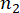 ומציין
ומציין 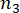 את מספר הכמויות הפיזיקליות הנוגעות בדבר ו-DOF של המבנה ובולמי MR המותקנים במבנה, בהתאמה.
את מספר הכמויות הפיזיקליות הנוגעות בדבר ו-DOF של המבנה ובולמי MR המותקנים במבנה, בהתאמה. 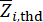 ומציין
ומציין  את הסף של
את הסף של 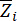 ו
ו - ;
- ;  מציין את ההסתברות של האירוע האקראי.
מציין את ההסתברות של האירוע האקראי.
1.3 אופטימיזציה של פרמטרים
היחס בין המשרעות של  ומשפיע
ומשפיע 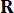 מאוד על יעילות הבקרה38 בשיטת בקרת המשוב. לכן, כדי להשיג את יעילות הבקרה הטובה ביותר,
מאוד על יעילות הבקרה38 בשיטת בקרת המשוב. לכן, כדי להשיג את יעילות הבקרה הטובה ביותר, וצריך
וצריך 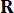 לייעל. חוץ מזה, כשיטת בקרה מבוססת בולם MR, יעילות הבקרה מושפעת גם מפרמטרי המכשיר,
לייעל. חוץ מזה, כשיטת בקרה מבוססת בולם MR, יעילות הבקרה מושפעת גם מפרמטרי המכשיר, 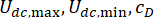 ב-Eq. (6). להשגת האמינות האופטימלית של מערכת בקרת המבנה, הקריטריון מבוסס האמינות מוצע ב-Eq. (25).
ב-Eq. (6). להשגת האמינות האופטימלית של מערכת בקרת המבנה, הקריטריון מבוסס האמינות מוצע ב-Eq. (25).

איור 1: תרשים זרימה של אופטימיזציה של פרמטרים עבור בקרת מבנה חצי-אקטיבי אופטימלי סטוכסטי עם קיזוז עיכוב זמן. קיצורים: GDEE = משוואה דיפרנציאלית כללית של האירוע; PDF = פונקציית צפיפות הסתברות. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
לסיכום, נדרשים שני שלבים לביצוע בקרת מבנה חצי אקטיבית סטוכסטית אופטימלית המבוססת על בולמי MR עם פיצוי עיכוב זמן:
1.3.1 מזעור פונקציית  העלות המוצגת במשוואה (7), מושגת לוגיקת משוב המצב במובן של דגימות, כלומר, Eq. 12)
העלות המוצגת במשוואה (7), מושגת לוגיקת משוב המצב במובן של דגימות, כלומר, Eq. 12)
1.3.2 מזעור פונקציית  ביצועים מבוססת אמינות, מושגים הפרמטרים האופטימליים במובן של סטטיסטיקה. איור 1 מציג את תרשים הזרימה של האופטימיזציה של הפרמטרים של הבקר בשלב 1.3.2.
ביצועים מבוססת אמינות, מושגים הפרמטרים האופטימליים במובן של סטטיסטיקה. איור 1 מציג את תרשים הזרימה של האופטימיזציה של הפרמטרים של הבקר בשלב 1.3.2.
השלבים הבאים בשלב 1.3.2, הכוללים שתי שכבות של לולאות, הם כדלקמן:
1.3.2.1 חלוקת המרחב המוקצה להסתברות של עירורים סטוכסטיים, המאופיין על ידי וקטור 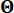 הפרמטר הסטוכסטי , מאפשרת זיהוי של קבוצה של נקודות
הפרמטר הסטוכסטי , מאפשרת זיהוי של קבוצה של נקודות  מייצגות יחד עם ההסתברויות שהוקצו להןPq's. גישה זו מאפשרת ליצור בקלות תהליכי דגימה לעירור הסטוכסטי, המסומן כ
מייצגות יחד עם ההסתברויות שהוקצו להןPq's. גישה זו מאפשרת ליצור בקלות תהליכי דגימה לעירור הסטוכסטי, המסומן כ 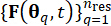 -,
-,
1.3.2.2 לאופטימיזציה של הפרמטרים של מערכת בקרת המבנה החצי אקטיבית, אתחל או עדכן את הערכים של משקלי עלות-פונקציה  ו
ו 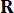 -. לאחר מכן מחושב כוח בקרת משוב המצב המשויך עם עיכוב הזמן, ראה Eq. (12).
-. לאחר מכן מחושב כוח בקרת משוב המצב המשויך עם עיכוב הזמן, ראה Eq. (12).
1.3.2.3 השגת פונקציות צפיפות ההסתברות (PDFs) של תגובות מבניות וכוח בקרה על ידי פתרון ה-GDEEs המוצגים ב-Eqs. (17)–(20):
האופטימיזציה היא השלמה לא מקוונת אך לא מקוונת. ביישום השיטה המוצעת במערכות בקרת מבנה אמיתיות, האופטימלי  והושג
והושג 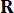 , והאופטימיזציה אינה נחוצה בתהליך היישום האמיתי.
, והאופטימיזציה אינה נחוצה בתהליך היישום האמיתי.
ניתוח דינמי דטרמיניסטי של מערכת בקרת המבנה הפעילה למחצה הנתונה לעירור דגימה, שבאמצעותו מחושבים הכמויות הפיזיקליות 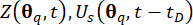 הנוגעות בדבר ונגזרותיהן
הנוגעות בדבר ונגזרותיהן .
.
על ידי שימוש בשיטת הפרש סופי, כגון סכימת Lax-Wendroff ששונתה עם תכונות הפחתת שונות כוללת (TVD), ניתן לפתור את המשוואות הדיפרנציאליות המוכללות (GDEEs), וניתן לגזור פתרונות מספריים לפונקציות 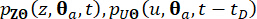 צפיפות ההסתברות המשותפת.
צפיפות ההסתברות המשותפת.
אם נחזור על שני השלבים לעיל של ניתוח דינמי דטרמיניסטי ושיטת ההפרש הסופי, ומעבר על כל הנקודות המייצגות 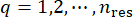 , ניתן לקבל את פונקציות צפיפות ההסתברות על ידי סיכום:
, ניתן לקבל את פונקציות צפיפות ההסתברות על ידי סיכום:
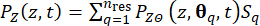 (23)
(23)
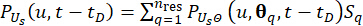 (24)
(24)
כאשר 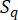 מייצג את מדידת השטח של תת-הדומיין המשויך לנקודת
מייצג את מדידת השטח של תת-הדומיין המשויך לנקודת  הדגימה . השיטה המשמשת לפתרון המשוואה הדיפרנציאלית המוכללת של האירוע (GDEE) ידועה בשם שיטת התפתחות צפיפות ההסתברות (PDEM)42.
הדגימה . השיטה המשמשת לפתרון המשוואה הדיפרנציאלית המוכללת של האירוע (GDEE) ידועה בשם שיטת התפתחות צפיפות ההסתברות (PDEM)42.
1.3.2.4 קובצי ה-PDF של הכמויות הפיזיקליות הרלוונטיות משמשים להערכת מהימנותן, אשר משולבות לאחר מכן בפונקציית  הביצועים של הקריטריון ההסתברותי.
הביצועים של הקריטריון ההסתברותי.
1.3.2.5 העריכו אם התקיימו קריטריוני הסיום לתהליך אופטימיזציית הפרמטרים. אם התנאים אינם מתקיימים, חזור לשלב 1.3.2.2; אם כן, ניתן לקבוע את הפרמטרים האופטימליים למערכת הבקרה המושהית בזמן. בעבודה זו, ארגז הכלים של האלגוריתם הגנטי (GA) ב-MATLAB משמש לאופטימיזציה של פרמטרים, מה שמקל על עדכוני פרמטרים ומגדיר את תנאי הסיום. על ידי אלגוריתם גנטי, ניתן להשיג את הערכים האופטימליים תוך עשר איטרציות, וההתכנסות יציבה ללא בעיות מינימום מקומיות. למרות שהעלות החישובית של GA גדולה יותר מאופטימיזציה של נחיל חלקיקים או שיטות מבוססות שיפוע, ה-GA טוב בהתמודדות עם בעיות מורכבות ובלתי ניתנות להבחנה, כמו זו שבכתב יד זה. לכן, ה-GA מיושם. ומכיוון שמאפיין ההתכנסות המהירה, העלות החישובית של GA מקובלת.
1.3.2.6 כדי להשיג בקרת אמינות אופטימלית, מנוסחת פונקציית  הביצועים הבאה. מזער
הביצועים הבאה. מזער  כדי לקבוע את הערכים האופטימליים של פרמטרים
כדי לקבוע את הערכים האופטימליים של פרמטרים 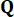 ו
ו  :
:
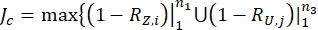 } (25)
} (25)
 (26)
(26)
כאמור, מטריצות השקלול של הבקר הן סימטריות, כאשר האלמנטים במטריצה 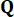 תואמים את המשקולות שהוקצו לתזוזה, מהירות ואינטראקציה ביניהם, ואילו האלמנטים במטריצה
תואמים את המשקולות שהוקצו לתזוזה, מהירות ואינטראקציה ביניהם, ואילו האלמנטים במטריצה  מייצגים את המשקולות הקשורות לכוח הבקרה. בהתבסס על הממצאים ממחקרים קודמים38, נצפה כי לשינוי התצורות של משקולות
מייצגים את המשקולות הקשורות לכוח הבקרה. בהתבסס על הממצאים ממחקרים קודמים38, נצפה כי לשינוי התצורות של משקולות 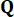 העלות-פונקציה יש
העלות-פונקציה יש  השפעה מינימלית על יעילות הבקרה. כתוצאה מכך, תצורה פשוטה מאומצת במחקר זה, כמתואר להלן:
השפעה מינימלית על יעילות הבקרה. כתוצאה מכך, תצורה פשוטה מאומצת במחקר זה, כמתואר להלן:
 ,
,  (27)
(27)
כאשר 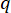 מציין את המקדם של מטריצת שקלול המצב שיש להגדיר;
מציין את המקדם של מטריצת שקלול המצב שיש להגדיר; 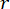 מציין את המקדם של מטריצת שקלול הבקרה שיש להגדיר;
מציין את המקדם של מטריצת שקלול הבקרה שיש להגדיר;  מציין את מטריצת הזהות. אפקט הבקרה מושפע מהיחס בין
מציין את מטריצת הזהות. אפקט הבקרה מושפע מהיחס בין 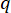 ל
ל 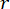 אך לא מהערכים עצמם. חוץ מזה,
אך לא מהערכים עצמם. חוץ מזה, 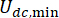 ב-Eq. (6) מציין את הכוח הקולומבי המינימלי של בולם ה-MR, מה שאומר שכאשר
ב-Eq. (6) מציין את הכוח הקולומבי המינימלי של בולם ה-MR, מה שאומר שכאשר 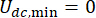 הכניסה הנוכחית בבולם היא אפס. לאחר מכן, ניתן לבטא את Eq. (26) כ:T
הכניסה הנוכחית בבולם היא אפס. לאחר מכן, ניתן לבטא את Eq. (26) כ:T
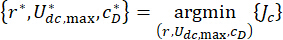 (28)
(28)
היכן 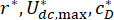 נמצאים מקדמי הדאגה האופטימליים. כדי להפוך אותם לסבירים בהנדסה, הטווחים האופטימליים שלהם מבוססים על כושר הייצור של מפעלי הבולמים MR.
נמצאים מקדמי הדאגה האופטימליים. כדי להפוך אותם לסבירים בהנדסה, הטווחים האופטימליים שלהם מבוססים על כושר הייצור של מפעלי הבולמים MR.
ברור שהפרמטרים האופטימליים המתקבלים על ידי Eq. (28) שומרים על יעילות הבקרה האופטימלית של אלגוריתם הבקרה החצי אקטיבי המוצע עם עיכוב זמן, המאפשר למערכת בקרת המבנה להשיג את האמינות האופטימלית המאוזנת הנתונה לעירורים סטוכסטיים.
2. מקרה בוחן
כדי לנתח את היעילות של שיטת הבקרה החצי אקטיבית המוצעת עם פיצוי עיכוב זמן עבור בולם MR, מבנה מסגרת גזירה מישורי בן קומה אחת המחובר לבולם MR היה נתון לתנועת הקרקע הסייסמית הסטוכסטית האופקית, כפי שמוצג באיור 2. הפרמטרים של מערכת המבנה המבוקרת למחצה הם כדלקמן: מסת 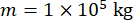 מבנה , תדר
מבנה , תדר 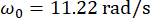 מעגלי טבעי , יחס
מעגלי טבעי , יחס 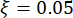 שיכוך . על פי ניסיון העבר ומאזני הבולמים הקיימים בשוק, ערכי הסף של תזוזה מבנית, מהירות, תאוצה וכוח בקרה הם 10 מ"מ, 100 מ"מ לשנייה, 1,500 מ"מ לשנייה2 ו-150 קילו-ניוטון, בהתאמה. לייצוג תנועת הקרקע הסייסמית הסטוכסטית, נעשה שימוש במודל תנועת הקרקע הסטוכסטית המונעת פיזית43:
שיכוך . על פי ניסיון העבר ומאזני הבולמים הקיימים בשוק, ערכי הסף של תזוזה מבנית, מהירות, תאוצה וכוח בקרה הם 10 מ"מ, 100 מ"מ לשנייה, 1,500 מ"מ לשנייה2 ו-150 קילו-ניוטון, בהתאמה. לייצוג תנועת הקרקע הסייסמית הסטוכסטית, נעשה שימוש במודל תנועת הקרקע הסטוכסטית המונעת פיזית43:
 (29)
(29)
כאשר 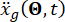 מייצג את תנועת הקרקע במרחב הזמן באתר ההנדסי, ומציין
מייצג את תנועת הקרקע במרחב הזמן באתר ההנדסי, ומציין 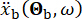 את תנועת הקרקע בתחום התדר בסלע האם. הווקטור
את תנועת הקרקע בתחום התדר בסלע האם. הווקטור 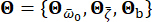 מאפיין את האופי הסטוכסטי של תנועת הקרקע על פני האתר ההנדסי. הפרמטרים
מאפיין את האופי הסטוכסטי של תנועת הקרקע על פני האתר ההנדסי. הפרמטרים 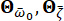 הם משתנים סטוכסטיים המתארים את מאפייני קרקע האתר, כולל התדירות
הם משתנים סטוכסטיים המתארים את מאפייני קרקע האתר, כולל התדירות 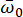 השולטת והשיכוך
השולטת והשיכוך 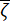 המקביל. הווקטור
המקביל. הווקטור 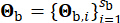 מייצג את האופי הסטוכסטי של תנועת הקרקע בסלע האם, המושפע מתכונות המקור ומנתיב ההתפשטות, תוך
מייצג את האופי הסטוכסטי של תנועת הקרקע בסלע האם, המושפע מתכונות המקור ומנתיב ההתפשטות, תוך 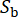 ציון מספר המשתנים הסטוכסטיים המעורבים בשלב זה.
ציון מספר המשתנים הסטוכסטיים המעורבים בשלב זה. 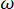 מתייחס לתדר המעגלי, ו-i היא היחידה הדמיונית.
מתייחס לתדר המעגלי, ו-i היא היחידה הדמיונית.
התדירות  השולטת ויחס
השולטת ויחס 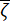 השיכוך המקביל של האתר ההנדסי הם פרמטרים מרכזיים המאפיינים את התכונות הדינמיות של קרקע האתר. ניתן לקבוע את ההתפלגות ההסתברותית והפרמטרים הסטטיסטיים של כמויות אלה על סמך רשומות תאוצה סייסמיות שנאספו מסוג מסוים של אתרים הנדסיים. למטרות המחשה, נלקחה בחשבון מחלקת אתר עם טווח מהירות גלי גזירה של [150, 250] מטר לשנייה, ותקופת התכנון האופיינית לתנועת הקרקע נקבעה ל-0.45 שניות.
השיכוך המקביל של האתר ההנדסי הם פרמטרים מרכזיים המאפיינים את התכונות הדינמיות של קרקע האתר. ניתן לקבוע את ההתפלגות ההסתברותית והפרמטרים הסטטיסטיים של כמויות אלה על סמך רשומות תאוצה סייסמיות שנאספו מסוג מסוים של אתרים הנדסיים. למטרות המחשה, נלקחה בחשבון מחלקת אתר עם טווח מהירות גלי גזירה של [150, 250] מטר לשנייה, ותקופת התכנון האופיינית לתנועת הקרקע נקבעה ל-0.45 שניות.
הפרמטרים  הקריטיים טופלו
הקריטיים טופלו 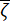 כמשתנים סטוכסטיים בלתי תלויים זה בזה, שניהם בעקבות התפלגות לוג-נורמלית לזיהוי פרמטרים. הפרמטרים הסטטיסטיים היו כדלקמן: הממוצע של
כמשתנים סטוכסטיים בלתי תלויים זה בזה, שניהם בעקבות התפלגות לוג-נורמלית לזיהוי פרמטרים. הפרמטרים הסטטיסטיים היו כדלקמן: הממוצע של  ,
, 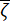 היה 12 rad/s ו-0.1, בהתאמה. מקדמי השונות של
היה 12 rad/s ו-0.1, בהתאמה. מקדמי השונות של  ו
ו 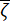 - היו 0.42 ו-0.35, בהתאמה. תנועת הקרקע בסלע האם תוכננה כתהליך רעש לבן גאוס עם משרעת פורייה של 0.20 מטר לשנייה2, המקבילה לתאוצה קרקעית שיא של 0.11 גרם. זווית הפאזה ששימשה ליצירת תנועת הסלע צוינה כ
- היו 0.42 ו-0.35, בהתאמה. תנועת הקרקע בסלע האם תוכננה כתהליך רעש לבן גאוס עם משרעת פורייה של 0.20 מטר לשנייה2, המקבילה לתאוצה קרקעית שיא של 0.11 גרם. זווית הפאזה ששימשה ליצירת תנועת הסלע צוינה כ 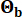 -. לכן, Sb = 1 ו-
-. לכן, Sb = 1 ו- 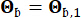 . גישה זו יכולה להיחשב כמידול תנועות קרקע סטוכסטיות מותנות עם הסתברות חריגה נתונה44. ההנחה של התפלגות לוג-נורמלית נמצאת בשימוש נרחב במודלים של תנועת קרקע בשל יכולתה ללכוד את האופי המוטה של פרמטרים של תנועת קרקע נצפית.
. גישה זו יכולה להיחשב כמידול תנועות קרקע סטוכסטיות מותנות עם הסתברות חריגה נתונה44. ההנחה של התפלגות לוג-נורמלית נמצאת בשימוש נרחב במודלים של תנועת קרקע בשל יכולתה ללכוד את האופי המוטה של פרמטרים של תנועת קרקע נצפית.
כדי להעריך את הרגישות של הנחה זו, הניתוחים הנוספים המשתמשים בהתפלגויות הסתברותיות חלופיות, כולל ההתפלגות הנורמלית וההתפלגות הגמא נערכו במחקרים אחרים45,46. הממצאים מצביעים על כך שבעוד שהמגמות הכלליות נשארות עקביות, ההתפלגות הלוג-נורמלית מספקת את ההתאמה הטובה ביותר לנתונים שנצפו, במיוחד ללכידת התנהגות הזנב של מדדי עוצמת תנועת הקרקע
בזכות שיטת הספירות המשיקות47, נבחר אוסף של 221 נקודות מייצגות עם הסתברויות מוקצות קשורות וסונתזו תאוצות קרקע מייצגות. תדר הדגימה היה 50 הרץ, ומשך תנועות הקרקע היה 20.48 שניות. כדי להקצות עוצמה לא נייחת לתנועת הקרקע המדומה, נעשה שימוש בפונקציית אפנון אחידה והניסוח שלה היה כדלקמן42:
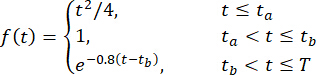 (30)
(30)
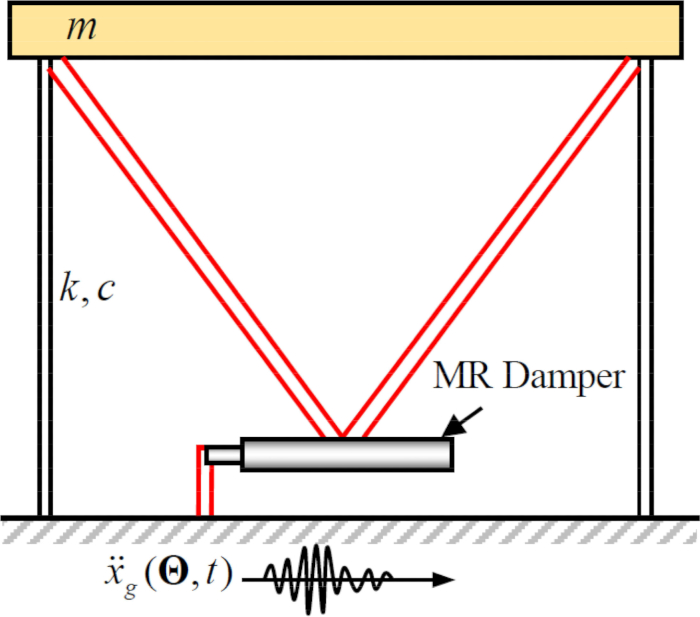
כאשר 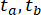 לוקחים 2 ו -16 שניות, בהתאמה.
לוקחים 2 ו -16 שניות, בהתאמה.
הממוצע וסטיית התקן של תנועת הקרקע הסייסמית הסטוכסטית, והיסטוריית זמן של תנועת קרקע סייסמית מייצגת מוצגים באיור 3. משרעת הממוצע (0.06 m/s2) הייתה ~8% מהמשרעת של סטיית התקן (0.8 m/s2), מה שמצביע על כך שמודל תנועת הקרקע הסטוכסטית המונעת פיזית הציג את התכונה של ממוצע אפס. בינתיים, תנועת הקרקע הסייסמית הפגינה התנהגויות לא נייחות יוצאות דופן הן בתחום הזמן והן בתחום התדר.
איור 2: שרטוט של מסגרת גזירה חד-קומתית עם בולם מגנטורולוגי.  לציין מסת מבנה, יחס שיכוך ונוקשות;
לציין מסת מבנה, יחס שיכוך ונוקשות; 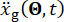 מציין את העירור הסייסמי הסטוכסטי. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
מציין את העירור הסייסמי הסטוכסטי. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
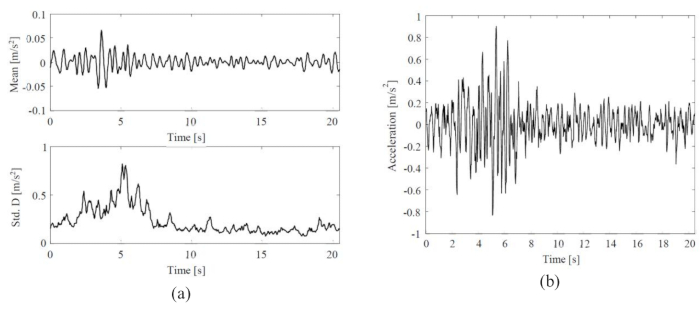
איור 3: סטטיסטיקות ודגימות מייצגות של תנועות קרקע סייסמיות נבחרות. (א) ממוצע וסטיית תקן של תנועת קרקע סייסמית סטוכסטית; (ב) היסטוריית זמן של תנועת קרקע סייסמית מייצגת. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
2.1 ניתוח השפעה של עיכוב זמן
כדי לנתח את השפעת עיכוב הזמן על יעילות הבקרה החצי אקטיבית של בולם MR, איור 4 מציג את התזוזה, המהירות והתאוצה RMS (תגובת שורש-ממוצע-ריבוע) של המבנה המבוקר. יחס מטריצת השקלול ופרמטרי הבולם היו 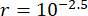 ,
, 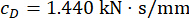 ו
ו 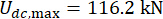 - , שהם התוצאות האופטימליות ללא עיכוב זמן38. התגובות של המבנה המבוקר עם עיכוב זמן היו גדולות יותר מהמבנה המבוקר ללא עיכוב בזמן, והשפעת עיכוב הזמן על אפקט הבקרה ייצגה מחזוריות יחד עם עליית עיכוב הזמן. מכיוון ששיטת הבקרה החצי אקטיבית עם בולם MR היא סוג של שיטת משוב, מחזוריות ההשפעה נחשבה קשורה לתקופה הטבעית של המבנה המבוקר (T = 0.56 שניות).
- , שהם התוצאות האופטימליות ללא עיכוב זמן38. התגובות של המבנה המבוקר עם עיכוב זמן היו גדולות יותר מהמבנה המבוקר ללא עיכוב בזמן, והשפעת עיכוב הזמן על אפקט הבקרה ייצגה מחזוריות יחד עם עליית עיכוב הזמן. מכיוון ששיטת הבקרה החצי אקטיבית עם בולם MR היא סוג של שיטת משוב, מחזוריות ההשפעה נחשבה קשורה לתקופה הטבעית של המבנה המבוקר (T = 0.56 שניות).
בהשוואה לתגובות של מבנה בלתי מבוקר, שמתוכם התזוזה, המהירות והתאוצה המקסימלית של MRS היו 24.6 מ"מ, 270.0 מ"מ לשנייה ו-3111.3 מ"מ לשנייה2, המבנה הנשלט על ידי בולם MR השיג אפקט בולט. בניגוד לחוסר היציבות של המבנה המבוקר הפעיל עם עיכוב זמן25, שיטת הבקרה החצי אקטיבית המבוססת על בולם MR עדיין השיגה השפעה מסוימת גם עם עיכוב בזמן.

איור 4: ריבועי השורש הממוצע המקסימליים של תגובות המבנה המבוקר עם הזמן. (א) עקירה; (ב) מהירות; (ג) תאוצה. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
כדי לנתח את השפעת עיכוב הזמן על האמינות של מבנה מבוקר חצי אקטיבי, איור 5 מציג את האמינות של תזוזה, מהירות ותאוצה עם עיכוב זמן הולך וגובר. האמינות של תגובות מבנה מבוקר עם כל עיכוב זמן הייתה נמוכה מהערכים ללא עיכוב זמן, מה שאומר שהאמינות של המבנה המבוקר ירדה על ידי עיכוב זמן. בינתיים, בדומה ל-RMS המקסימלי, אפקט בקרת האמינות הראה מחזוריות עם עיכוב זמן הולך וגובר. יתר על כן, האמינות של המבנה המבוקר, עם או בלי עיכוב בזמן, הייתה גבוהה יותר מהערכים של מבנים בלתי מבוקרים עם אמינות של תזוזה, מהירות ותאוצה 0.0954, 0.1058 ו-0.1111.
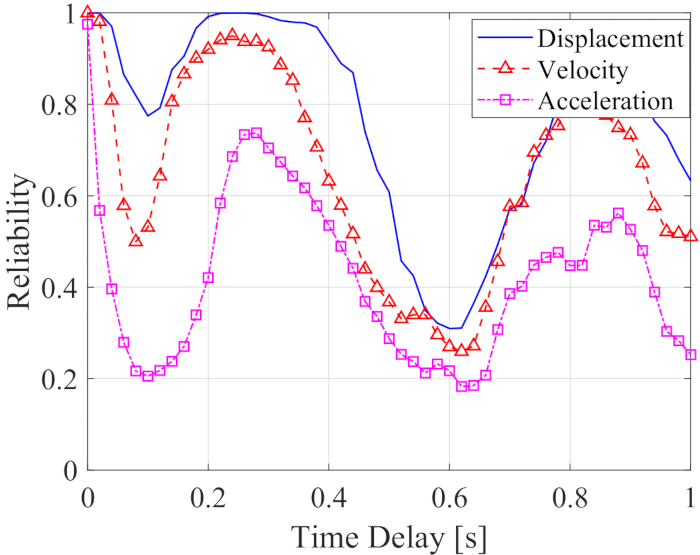
איור 5: אמינות התגובות של מבנה מבוקר עם עיכוב זמן הולך וגדל. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
לסיכום, תגובות המבנה הופחתו על ידי שיטת הבקרה החצי אקטיבית. עם זאת, יעילות הבקרה, ללא קשר ל-RMS או לאמינות, של שיטת הבקרה החצי אקטיבית פחתה על ידי עיכוב הזמן. לכן, יש צורך לפצות על עיכוב הזמן.
2.1.1 ניתוח שיטת פיצוי עיכוב הזמן
לניתוח האפקטיביות של שיטת פיצוי עיכוב הזמן המוצעת, היסטוריית הזמן של RMS של תזוזה, מהירות ותאוצה עבור מערכת לא מבוקרת (Unc), מערכת מושהית בזמן עם מבוקרת ללא פיצוי (TDN-SAC-PSO) ומערכת מושהית בזמן עם מבוקרת קיזוז (TDC-SAC-PSO) מושווים באיור 6, שם עיכוב הזמן היה 0.1 שניות. הפרמטרים של מטריצת השקלול ושיטת הבקרה החצי אקטיבית זהים לשלב 2.1.

איור 6: השוואת היסטוריית זמן שורש-ממוצע-ריבוע של מבנים הנשלטים בשיטות שונות. (א) עקירה; (ב) מהירות; (ג) תאוצה; (ד) כוח בקרה. קיצורים: unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; TDN -SAC-PSO = מערכת מושהית בזמן עם אי-קיזוז מבוקר. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
שתי שיטות הבקרה הפחיתו משמעותית את תגובות המבנה בהשוואה למבנה הבלתי מבוקר, וחשפו את היתרונות של שיטת הבקרה מבוססת בולם MR. בהשוואה למבנה הבלתי מבוקר, ה-RMS המקסימלי של תזוזה, מהירות ותאוצה יורד ב-75.79%, 73.75% ו-61.22% בשיטת TDN-SAC-PSO. יתר על כן, עם פיצוי עיכוב הזמן, התגובות של המבנה המבוקר מופחתות ב-82.59%, 80.40% ו-73.04% בשיטת TDC-SAC-PSO. ה-RMS המרבי של כוח הבקרה בשיטת TDC-SAC-PSO ירד ב-8.43% בהשוואה לשיטת TDN-SAC-PSO, אם כי תגובות הרטט של השיטה הראשונה היו נמוכות מהשנייה. הניתוח לעיל מצביע על כך שהשפעת עיכוב הזמן על שיטת הבקרה המבוססת על בולם MR פחתה למעשה על ידי שיטת הפיצוי, המראה את הצורך בפיצוי עיכוב זמן עבור שיטת בקרה חצי אקטיבית של בולם MR.

איור 7: השוואת PDF בזמנים אופייניים של תגובות מבנה. (א) עקירה; (ב) מהירות; (ג) תאוצה. קיצורים: PDF = פונקציית צפיפות הסתברות; Unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; TDN -SAC-PSO = מערכת מושהית בזמן עם אי-קיזוז מבוקר. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
כדי לחשוף באופן מקיף את ההשפעה של שיטת הפיצוי המוצעת על אי הוודאות של התגובות של המבנה המבוקר, השוואות פונקציית צפיפות ההסתברות (PDF) של תזוזה, מהירות ותאוצה בזמנים טיפוסיים, 3, 7 ו-11 שניות, מוצגות באיור 7. קובצי ה-PDF עבור שיטת TDN-SAC-PSO היו צרים יותר מאלה של המבנה הבלתי מבוקר, מה שאומר שאי הוודאות של תגובות המבנה פחתה בשיטת הבקרה הפעילה למחצה גם עם עיכוב בזמן. כאשר פיצו על עיכוב הזמן, קובצי ה-PDF של התגובות צומצמו עוד יותר. לכן, שיטת הפיצוי המוצעת נחוצה לשיפור אפקט הבקרה החצי אקטיבי.
| שיטת בקרה | הזחה | מהירות | תאוצה | כוח בקרה | ערך מינימלי |
| אונק | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
טבלה 1: תגובות רטט ואמינות כוח בקרה של מבנים הנשלטים בשיטות שונות. קיצורים: unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; TDN -SAC-PSO = מערכת מושהית בזמן עם אי-קיזוז מבוקר.
תגובות הרטט ואמינות כוח הבקרה של מבנים מבוקרי שיטה בלתי מבוקרים, TDC-SAC-PSO- ו-TDN-SAC-PSO מוצגים בטבלה 1. עם בקרת שיטת TDN-SAC-PSO, אמינות המבנה גדלה באופן דרמטי בהשוואה למבנה הבלתי מבוקר, מה שמאמת את היעילות של שיטת הבקרה מבוססת מנחת MR, גם עם הזמן. עם זאת, עם פיצוי עיכוב בזמן, האמינות גדלה משמעותית בהשוואה ללא פיצוי, במיוחד עבור התאוצה. ראוי לציין גם כי האמינות של תגובות שונות וכוח הבקרה הראו הבדלים משמעותיים בשיטת TDC-SAC-PSO. זה מצביע על כך שהערכים האופטימליים של פרמטרים קריטיים לבקרה ללא עיכוב זמן אינם אופטימליים לבקרה עם עיכוב זמן. כדי להשיג את אפקט הבקרה האופטימלי של תגובות הרטט וכוח הבקרה עם השפעת עיכוב הזמן, יש לבצע אופטימיזציה נוספת של הפרמטרים. בהתבסס על הניתוח לעיל, המסקנה היא ששיטת הבקרה החצי אקטיבית עם בולם MR יכולה להפחית ביעילות את תגובות הרטט של המבנה, בעוד שיש לייעל את הפרמטרים בגלל השפעת עיכוב הזמן.
2.2 אופטימיזציה של פרמטרים
כדי להשיג את הערכים האופטימליים של הפרמטרים, יושמה שיטת האופטימיזציה המשולבת המבוססת על קריטריון האמינות38. האופטימיזציה של פרמטרים קריטיים בוצעה עם  ,
, 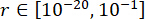 ,
, 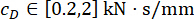 ,
, 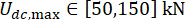 והזמנים הניתנים לכוונון של כוח הבולם MR s = 8. ארגז הכלים של GA בתוך MATLAB שימש ליישום האופטימיזציה.
והזמנים הניתנים לכוונון של כוח הבולם MR s = 8. ארגז הכלים של GA בתוך MATLAB שימש ליישום האופטימיזציה.
תוצאות האופטימיזציה של הפרמטרים הן 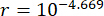 , ועבור
, ועבור  עיכוב
עיכוב 
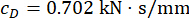 הזמן . איור 8 מציג את היסטוריית הזמן של RMS של תזוזה, מהירות, תאוצה וכוח בקרה עבור מבנים מבוקרים בשיטת TDC-SAC-PSO ושיטת SOSC-PSO. שיטת SOSC-PSO מציינת את שיטת הבקרה החצי אקטיבית עם פיצוי עיכוב זמן וערכי פרמטרים קריטיים אופטימליים.
הזמן . איור 8 מציג את היסטוריית הזמן של RMS של תזוזה, מהירות, תאוצה וכוח בקרה עבור מבנים מבוקרים בשיטת TDC-SAC-PSO ושיטת SOSC-PSO. שיטת SOSC-PSO מציינת את שיטת הבקרה החצי אקטיבית עם פיצוי עיכוב זמן וערכי פרמטרים קריטיים אופטימליים.

איור 8: היסטוריית זמן RMS של תזוזה, מהירות, תאוצה וכוח בקרה עבור מבנים מבוקרי שיטת TDC-SAC-PSO ושיטת TDC-SAC-PSO ו-SOSC-PSO. (א) עקירה; (ב) מהירות; (ג) תאוצה; (ד) כוח בקרה. קיצורים: unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; SOSC-PSO = שיטת בקרה חצי אקטיבית אופטימלית סטוכסטית עם פיצוי עיכוב זמן. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
מאיור 8, ניתן לראות שהשפעות הבקרה של שיטות TDC-SAC-PSO ו-SOSC-PSO הראו הבדל מועט. ה-RMS המקסימלי של מהירות התזוזה והתאוצה עבור השיטה הראשונה היה 81.60%, 81.21%, 73.62% מהמבנה הבלתי מבוקר ו-82.59%, 80.40%, 73.04% עבור השיטה השנייה. כדי לנתח באופן מקיף את מאפייני ההסתברות של התגובות עבור שתי שיטות הבקרה, איור 9 מציג את קובצי ה-PDF של תזוזה, מהירות ותאוצה עבור המבנים הבלתי מבוקרים, שיטת TDC-SAC-PSO ושיטת SOSC-PSO. לשתי שיטות הבקרה היו כמעט אותם קובצי PDF של תזוזה ומהירות בזמנים טיפוסיים. קובצי ה-PDF של התאוצה של שיטת SOSC-PSO היו צרים יותר מאלה של שיטת TDC-SAC-PSO, מה שאומר שאי הוודאות של התאוצה השיגה אפקט בקרה טוב יותר בשיטה הראשונה.
איור 9: השוואת קובצי PDF של תזוזה, מהירות ותאוצה עבור מבנים מבוקרים שונים. (א) עקירה; (ב) מהירות; (ג) תאוצה. קיצורים: קובצי PDF = פונקציות צפיפות הסתברות; Unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; SOSC-PSO = שיטת בקרה חצי אקטיבית אופטימלית סטוכסטית עם פיצוי עיכוב זמן. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
האמינות של תזוזה, מהירות, תאוצה וכוח בקרה עבור המבנים הבלתי מבוקרים והמבוקרים בשיטת TDC-SAC-PSO- ו- SOSC-PSO מוצגת בטבלה 2. שתי שיטות הבקרה השיגו עלייה משמעותית באמינות בהשוואה למבנה הבלתי מבוקר. אמינות התזוזה הראתה הבדל קטן בין שיטות TDC-SAC-PSO ו-SOSC-PSO. בעוד שאמינות התאוצה, האמינות הנמוכה ביותר של המבנה המבוקר, השיגה עלייה ניכרת. המשמעות היא ששיטת SOSC-PSO משיגה את אפקט הבקרה האופטימלי של האיזון.
| שיטת בקרה | הזחה | מהירות | תאוצה | כוח בקרה | ערך מינימלי |
| אונק | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
טבלה 2: אמינות למבנים הנשלטים בשיטות שונות. קיצורים: unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; SOSC-PSO = שיטת בקרה חצי אקטיבית אופטימלית סטוכסטית עם פיצוי עיכוב זמן.
נותחה היעילות של שיטת SOSC-PSO המוצעת עם עיכוב  בזמן. כדי לאמת עוד יותר את השיטה המוצעת לעיכובי זמן שונים, טבלה 3 מציגה את ערכי הפרמטרים האופטימליים ואת האמינות המתאימה לטווח
בזמן. כדי לאמת עוד יותר את השיטה המוצעת לעיכובי זמן שונים, טבלה 3 מציגה את ערכי הפרמטרים האופטימליים ואת האמינות המתאימה לטווח  עיכוב הזמן.
עיכוב הזמן.
| tD(s) | lg(r*) | CD(kN·s/mm) | U DC, מקסימום (kN) | הזחה | מהירות | תאוצה | כוח בקרה |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
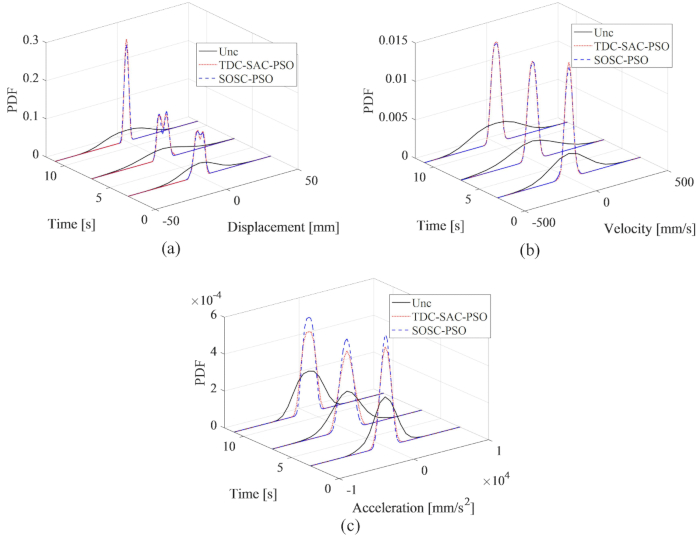
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| אונק | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
טבלה 3: ערכי הפרמטרים האופטימליים וערכי המהימנות המתאימים עבור עיכובי זמן שונים. 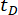 מציין עיכוב זמן;
מציין עיכוב זמן; 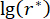 מציין את הערך הלוגריתמי האופטימלי של r,r מציין את מקדם מטריצת שקלול הבקרה;
מציין את הערך הלוגריתמי האופטימלי של r,r מציין את מקדם מטריצת שקלול הבקרה; 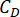 מציין את מקדם השיכוך הצמיג של בולם MR;
מציין את מקדם השיכוך הצמיג של בולם MR; 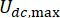 לציין את הכוחות הקולומביים המקסימליים והמינימליים של בולם MR.
לציין את הכוחות הקולומביים המקסימליים והמינימליים של בולם MR.
ניתן לראות כי האמינות של תזוזה, מהירות ותאוצה השתפרה בהשוואה למבנה הבלתי מבוקר, אפילו בנוכחות עיכוב בזמן, מה שמדגים את החוסן של השיטה המוצעת לקראת עיכובים כאלה. עם זאת, האמינות של התגובות המבניות בשיטת הבקרה המוצעת פחתה ככל שעיכוב הזמן גדל, מה שמצביע על כך שבעוד שניתן להפחית את ההשפעה של עיכוב הזמן על יעילות הבקרה, לא ניתן לבטל אותה במלואה. יש לציין כי האמינות של כוח הבקרה נותרה מעל 90% על פני עיכובים שונים בזמן.
3. דוגמה מספרית
כדי לאמת את שיטת SOSC-PSO המוצעת במבנה MDOF, נותח מבנה בן שש קומות עם שני בולמי MR המותקנים בקומה הראשונה והשלישית, כפי שמוצג באיור 10. הדגימות הסייסמיות שהופקו על ידי מודל סייסמי סטוכסטי בסעיף 2 יושמו, וספי האמינות של תזוזה, מהירות, תאוצה וכוח בקרה היו 20 מ"מ, 200 מ"מ לשנייה, 3,000 מ"מ לשנייה2 ו-200 קילו-ניוטון. שווים. (27) שימשו כמטריצת השקלול עם  . ארגז הכלים GA של MATLAB שימש לאופטימיזציה
. ארגז הכלים GA של MATLAB שימש לאופטימיזציה 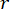 ,
,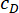 , ו
, ו 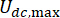 - , עם טווחים אופטימליים
- , עם טווחים אופטימליים 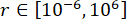 ,
, 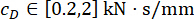 ו
ו 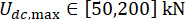 - .
- .

איור 10: מבנה בן שש קומות עם שני בולמי MR. קיצור: MR = מגנטורולוגי. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
3.1 ניתוח השפעה על עיכוב זמן
כדי לנתח את השפעת עיכוב הזמן על יעילות הבקרה של בולם ה-MR במבנה MDOF, איור 11 מציג את ה-RMS המקסימלי של תזוזה (תזוזה בין קומות), מהירות (מהירות בין קומות) ותאוצה (תאוצת סיפור) יחד עם עיכוב זמן עבור שיטת TDC-SAC-PSO. הפרמטרים היו 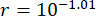 ,
, ועבור
ועבור 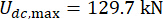 בולם ה-MR בקומה הראשונה;
בולם ה-MR בקומה הראשונה;  ועבור
ועבור 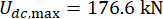 בולם ה-MR בקומה השלישית, שהן התוצאות האופטימליות ללא עיכוב בזמן. ה-RMS המקסימלי של תגובות המבנה המבוקר הראה תנודות תקופתיות יחד עם עיכוב בזמן. ה-RMS המקסימלי של תזוזה ומהירות היו בקומה הראשונה, התאוצה המקסימלית בקומה השישית. חוץ מזה, כל ה-MRS המקסימלי של תגובות עם כל עיכוב זמן היו גדולים מהערכים ללא עיכוב זמן, מה שאומר שעיכוב זמן מקטין את אפקט הבקרה של מנחת MR.
בולם ה-MR בקומה השלישית, שהן התוצאות האופטימליות ללא עיכוב בזמן. ה-RMS המקסימלי של תגובות המבנה המבוקר הראה תנודות תקופתיות יחד עם עיכוב בזמן. ה-RMS המקסימלי של תזוזה ומהירות היו בקומה הראשונה, התאוצה המקסימלית בקומה השישית. חוץ מזה, כל ה-MRS המקסימלי של תגובות עם כל עיכוב זמן היו גדולים מהערכים ללא עיכוב זמן, מה שאומר שעיכוב זמן מקטין את אפקט הבקרה של מנחת MR.

איור 11: RMS מקסימלי של תגובות יחד עם עיכוב זמן עבור המבנה המבוקר בשיטת TDC-SAC-PSO. (א) עקירה; (ב) מהירות; (ג) תאוצה. קיצורים: RMS = שורש-ממוצע-ריבוע; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
האמינות של תזוזה, מהירות ותאוצה יחד עם עיכוב זמן מוצגת באיור 12. אמינות המהירות והתאוצה מראות תנודות תקופתיות יחד עם עיכוב הזמן, בעוד שאמינות התזוזה ירדה באופן דרמטי יחד עם עיכוב הזמן; כל ערכי המהימנות בכל עיכוב זמן היו נמוכים מאלה ללא עיכוב זמן. לכן, שיטת פיצוי עיכוב הזמן נחוצה כדי להפחית את השפעת עיכוב הזמן על אמינות המבנה הנשלט על ידי בולם MR.
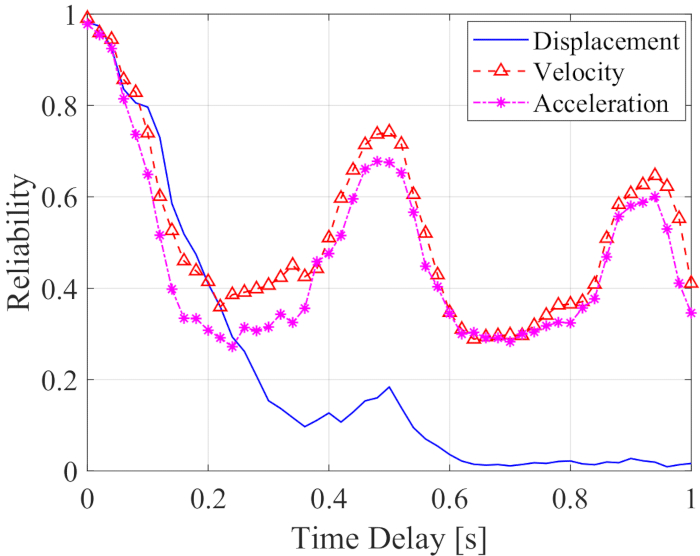
איור 12: מהימנות של תגובות מבנה מבוקרות יחד עם עיכוב בזמן. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
3.2 השפעת בקרה של פיצוי עיכוב זמן
בהתבסס על שיטת TDC-SAC-PSO המוצעת, נותח מבנה 6-DOF עם שני בולמי MR. איור 13 מציג את היסטוריית הזמן של RMS של תזוזה ותאוצה בקומות 1 ו-3 עבור מבנים מבוקרים בשיטת TDC-SAC-PSO ו-TDN-SAC-PSO. עיכוב הזמן היה 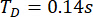 , ויחס
, ויחס 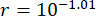 מטריצת השקלול; פרמטרי הבולם MR היו
מטריצת השקלול; פרמטרי הבולם MR היו  ,
, 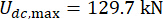 עבור הקומה הראשונה;
עבור הקומה הראשונה;  ועבור
ועבור 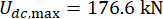 הקומה השלישית.
הקומה השלישית.

איור 13: היסטוריית זמן RMS של תזוזה ותאוצה בקומות 1 ו-3 עבור מבנים הנשלטים בשיטות שונות. (א) תזוזה בקומה הראשונה; (ב) תזוזה בקומה 3; (ג) האצה בקומה הראשונה; (ד) האצה בקומה 3. קיצורים: RMS = שורש-ממוצע-ריבוע; Unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; TDN -SAC-PSO = מערכת מושהית בזמן עם אי-קיזוז מבוקר. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
ה-RMS המקסימלי של תזוזה בקומות 1 ו-3 הופחת ב-35.42% ו-30.44% בשיטת TDN-SAC-PSO, שבה עיכוב הזמן לא פוצה. בעוד שעם פיצויים, ה-RMS המקסימלי של תזוזה בקומות 1 ו-3 הופחת ב-49.33% ו-53.39%, בהתאמה. ללא פיצוי, ה-RMS המקסימלי של האצה בקומות 1 ו-3 עלה ב-16.22% ו-2.88% אך ירד ב-25.77% ו-36.00%, בהתאמה, עם פיצוי. לכן, פיצוי עיכוב הזמן בשיטת בקרת בולם MR הכרחי להפחתת תגובות המבנה, במיוחד לתאוצה.
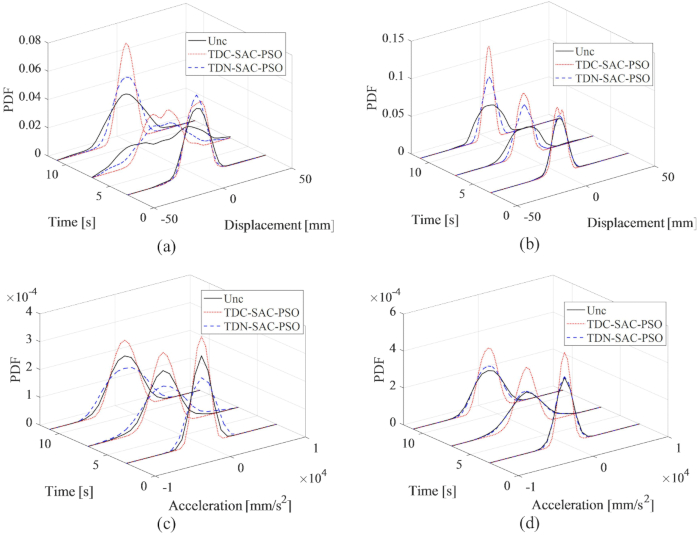
איור 14: קובצי PDF של תזוזה ותאוצה בקומות 1 ו-3 עבור שיטות בקרה שונות. (א) תזוזה בקומה הראשונה; (ב) תזוזה בקומה 3; (ג) האצה בקומה הראשונה; (ד) האצה בקומה 3. קיצורים: קובצי PDF = פונקציות צפיפות הסתברות; Unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; TDN -SAC-PSO = מערכת מושהית בזמן עם אי-קיזוז מבוקר. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
קובצי ה-PDF של תזוזה ותאוצה בקומות 1 ו-3 מוצגים באיור 14, וחושפים את השפעות הבקרה השונות של שיטות TDC-SAC-PSO ו-TDN-SAC-PSO בהשוואה למבנה הבלתי מבוקר. ללא פיצוי, קובצי ה-PDF של התזוזה בקומות 1 ו-3 היו עדיין צרים יותר מאלה של המבנה הבלתי מבוקר. יתר על כן, עם פיצוי על עיכוב הזמן, קובצי ה-PDF של התזוזה הפכו צרים יותר מאלה של המבנה הנשלט בשיטת TDN-SAC-PSO. בניגוד לתזוזה, ללא פיצוי, קובצי ה-PDF של התאוצה בקומה הראשונה בשיטת TDN-SAC-PSO היו רחבים יותר מאלה של המבנה הבלתי מבוקר. עם זאת, עם פיצוי, קובצי ה-PDF של התאוצה הן בקומה הראשונה והן בקומה השלישית היו צרים יותר מאלה של המבנה הבלתי מבוקר. לפיכך, הצורך בפיצוי עיכוב זמן מאומת להגברת הוודאות של תגובות המבנה, במיוחד עבור התאוצה.
| שיטת בקרה | הזחה | מהירות | תאוצה | כוח בקרהבקומה 1 | כוח בקרהבקומה 3 |
| אונק | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
טבלה 4: אמינות למבנים הנשלטים בשיטות שונות. קיצורים: unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; TDN -SAC-PSO = מערכת מושהית בזמן עם אי-קיזוז מבוקר.
ערכי האמינות של תזוזה, מהירות, תאוצה וכוח בקרה עם מערכות המבנה הנשלטות על ידי השיטות השונות מוצגים בטבלה 4. ערכי המהימנות של תגובות המבנה חושבו באמצעות שיטת הערך הקיצוני המקבילה25. על ידי בקרת שיטת TDN-SAC-PSO, אמינות התזוזה גדלה בהשוואה למבנה הבלתי מבוקר, בעוד שאמינות המהירות והתאוצה פחתה. עם פיצוי עיכוב זמן בשיטת TDC-SAC-PSO, אמינות התזוזה, המהירות והתאוצה גדלה משמעותית. חוץ מזה, ערכי האמינות של כוח הבקרה עבור שתי שיטות TDN-SAC-PSO ו- TDN-SAC-PSO נשמרים מספיק. לפיכך, שיטת בקרת פיצוי עיכוב הזמן המוצעת משיגה אפקט בקרה חיובי עבור המבנה הנשלט על ידי בולם MR.
3.3 אופטימיזציה של פרמטרים
כדי להשיג את אפקט הבקרה האופטימלי, הפרמטרים של שיטת הבקרה המוצעת עברו אופטימיזציה על סמך קריטריון האמינות. עם עיכוב 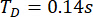 הזמן, התוצאה האופטימלית הייתה
הזמן, התוצאה האופטימלית הייתה 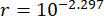 ;
; 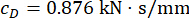 ועבור
ועבור  בולם MR בקומה הראשונה;
בולם MR בקומה הראשונה; 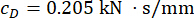 ועבור
ועבור 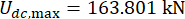 בולם MR השלישי.
בולם MR השלישי.
היסטוריית הזמן של RMS של תזוזה ותאוצה בקומות 1 ו-3 מוצגת באיור 15 שם משווים את השפעות הבקרה של שיטות TDC-SAC-PSO ו-SOSC-PSO והמבנה הבלתי מבוקר. עם בקרת בולם MR, עם או בלי פיצוי עיכוב זמן, ה-RMS של תזוזה ותאוצה ירד משמעותית. בשיטת SOSC-PSO, ה-RMS המקסימלי של תזוזה בקומות 1 ו-3 ירד ב-65.15% ו-63.16% ביחס למבנה הבלתי מבוקר, בהתאמה. בהשוואה לשיטת TDC-SAC-PSO, תגובת התזוזה הופחתה עוד יותר. ה-RMS המקסימלי של התאוצה בקומות 1 ו-3 יורד ב-23.39% וב-35.60% בשיטת SOSC-PSO. היה הבדל קטן בהשפעת הבקרה של תאוצה עבור שיטות SOSC-PSO ו-TDC-SAC-PSO, מה שמצביע על כך שהשפעת הבקרה של פיצוי עיכוב הזמן הייתה שונה עבור תזוזה ותאוצה.
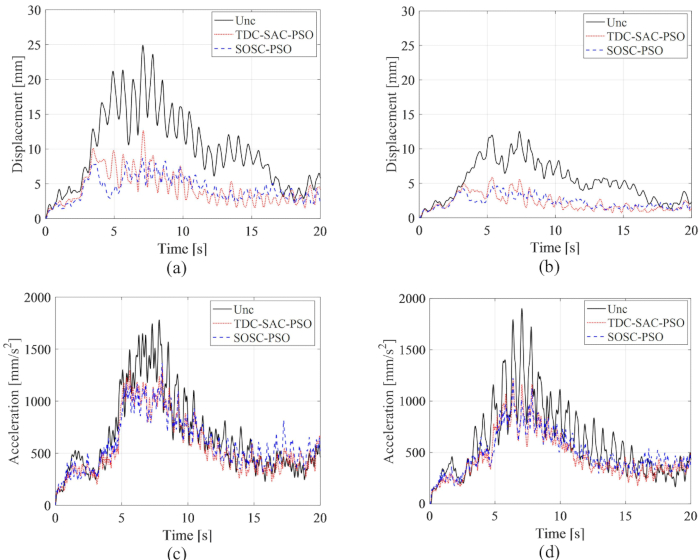
איור 15: היסטוריית זמן RMS של תזוזה ותאוצה בקומות 1 ו-3 עבור שיטות בקרה שונות. (א) תזוזה בקומה הראשונה; (ב) תזוזה בקומה 3; (ג) האצה בקומה הראשונה; (ד) האצה בקומה 3. קיצורים: RMS = שורש-ממוצע-ריבוע; Unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; SOSC-PSO = שיטת בקרה חצי אקטיבית אופטימלית סטוכסטית עם פיצוי עיכוב זמן. אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
קובצי ה-PDF של תזוזה ותאוצה בקומות 1 ו-3 מוצגים באיור 16; קובצי ה-PDF של תזוזה ותאוצה הצטמצמו בשיטות TDC-SAC-PSO ו-SOSC-PSO בהשוואה למבנה הבלתי מבוקר. חוץ מזה, קובצי ה-PDF של תזוזה ותאוצה עבור שיטת SOSC-PSO הצטמצמו עוד יותר בהשוואה לאלו של המבנה המבוקר בשיטת TDC-SAC-PSO. לכן, עם אופטימיזציה של פרמטרים, שיטת בקרת פיצוי עיכוב הזמן המוצעת השיגה אפקט בקרה טוב יותר מאשר ללא אופטימיזציה.

איור 16: קובצי PDF של תזוזה ותאוצה בקומות 1 ו-3 עבור שיטות בקרה שונות. (א) תזוזה בקומה הראשונה; (ב) תזוזה בקומה 3; (ג) האצה בקומה הראשונה; (ד) האצה בקומה 3. קיצורים: קובצי PDF = פונקציות צפיפות הסתברות; Unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; SOSC-PSO = שיטת בקרה חצי אקטיבית אופטימלית סטוכסטית עם פיצוי עיכוב זמן אנא לחץ כאן לצפייה בגרסה גדולה יותר של איור זה.
ערכי האמינות של תזוזה, מהירות, תאוצה וכוח בקרה מוצגים בטבלה 5. ערכי המהימנות של שיטת SOSC-PSO היו גבוהים יותר מאלה של שיטת TDC-SAC-PSO. בינתיים, כוח הבקרה עדיין שמר על אמינות מספקת. לפיכך, אופטימיזציה של פרמטרים נחוצה להשגת אפקט הבקרה הטוב ביותר עבור שיטת הבקרה המבוססת על בולם MR.
| שיטת בקרה | הזחה | מהירות | תאוצה | כוח בקרהבקומה 1 | כוח בקרהבקומה 3 |
| אונק | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
טבלה 5: אמינות למבנים הנשלטים בשיטות שונות. קיצורים: unc = לא מבוקר; TDC-SAC-PSO = מערכת מושהית בזמן עם פיצוי מבוקר; SOSC-PSO = שיטת בקרה חצי אקטיבית אופטימלית סטוכסטית עם פיצוי עיכוב זמן.
תוצאות
במטרה להשפיע על יעילות הבקרה של השיטה המבוססת על מנחת MR, מוצעת במאמר זה שיטת בקרה חצי אקטיבית עם פיצוי עיכוב זמן. בשיטה המוצעת, הפרמטרים הקריטיים מותאמים על סמך קריטריון האמינות. על ידי השוואת יעילות הבקרה, מתייחסים למסקנות הבאות:
(1) שיטת הבקרה החצי אקטיבית...
Discussion
עם הצגת תיאוריית הבקרה האופטימלית הסטוכסטית הפיזיקלית (PSO), מוצעת במאמר זה שיטת בקרה סטוכסטית אופטימלית למחצה עם פיצוי עיכוב זמן (SOSC-PSO), שנועדה לשמור על אמינות המבנים הנשלטים על ידי בולמי MR. כדי לפצות על עיכוב הזמן בשיטה המוצעת, כוח הבקרה הפעיל למחצה נגזר כפונקציה של לא רק ...
Disclosures
לכל המחברים אין ניגודי אינטרסים להצהיר עליהם.
Acknowledgements
המחברים מודים בהכרת תודה על תמיכתה של הקרן למדעי הטבע של מחוז הביי (מענק מס' E2023210007).
Materials
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
References
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Reprints and Permissions
Request permission to reuse the text or figures of this JoVE article
Request PermissionThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. All rights reserved