JoVE 비디오를 활용하시려면 도서관을 통한 기관 구독이 필요합니다. 전체 비디오를 보시려면 로그인하거나 무료 트라이얼을 시작하세요.
Research Article
Time Delay를 고려한 Magnetorheological Dampers를 기반으로 한 Stochastic Semi-active Control Method of Structure
요약
본 논문에서는 MR 댐퍼에 의해 제어되는 구조물의 신뢰성을 유지하도록 설계된 SOSC-PSO(Time Delay Compensation)를 사용한 확률적 최적 반능동 제어 방법을 제안합니다.
초록
반능동 제어 시스템에서 MR(Magnetorheological) 댐퍼를 사용하는 것은 피드백 프로세스로 인한 시간 지연이라는 주요 과제에 직면해 있으며, 이는 확률적 여기 하에서 토목 공학 구조물의 신뢰성을 감소시킵니다. 이 논문은 이 문제를 해결하고 구조적 신뢰성을 유지하기 위해 물리적 확률 최적 제어 이론(PSO)을 활용하여 시간 지연 보상(SOSC-PSO)을 사용하는 확률적 최적 반능동 제어 방법을 제안합니다. 제안된 방법은 반능동 제어력을 현재 상태와 이전 상태 모두의 함수로 도출하여 제어 프로세스의 시간 지연을 보상합니다. 제어 효율성을 최적화하기 위해 주요 매개변수는 시스템의 신뢰성 기준에 따라 조정됩니다. 확률적 지진 가진(stochastic seismic excitations) 하에서 단일 자유도 및 다중 자유도 구조에 대한 검증 분석은 시간 지연이 MR 댐퍼의 성능을 크게 손상시킨다는 것을 보여줍니다. 그러나 시간 지연 보상이 있는 SOSC-PSO 방법은 제어 효율성을 크게 향상시키고, 최적화된 매개변수를 통해 매개변수 최적화가 없는 방법을 넘어 구조 제어 시스템의 신뢰성을 향상시킵니다.
서문
지진 및 극심한 바람과 같은 재앙적인 사건에 직면하여 엔지니어링 구조물의 성능을 개선하는 것은 토목 공학 커뮤니티의 주요 관심사로 남아 있습니다. 진동을 줄이기 위한 효과적인 기술인 구조 제어는 이러한 구조물의 안전성과 기능을 모두 향상시키는 것으로 입증되었습니다 1,2,3. 지난 수십 년 동안 이를 위해 다양한 첨단 방법과 기술이 개발되었습니다. 이러한 방법은 제어 장치를 구동하는 데 사용되는 에너지 유형에 따라 능동, 반 능동, 수동 및 하이브리드 제어 시스템의 네 가지 범주로 크게 분류 할 수 있습니다 4,5,6,7.
능동 제어에서 필요한 제어력은 제어 장치를 통해 직접 적용되므로 상당한 양의 에너지가 필요합니다 8,9,10. 반면에, 반능동 제어(Semi-active control)는 제어 신호에 기초하여 제어 장치의 특성(예: 댐핑 또는 강성)을 조정하는 것을 포함하며, 능동 시스템11에 비해 훨씬 적은 에너지를 필요로 한다. 대조적으로, 수동 제어는 시스템에 외부 에너지가 입력되지 않는 에너지 소산에 의존합니다 12,13,14. 하이브리드 시스템은 능동/반능동 및 수동 제어 전략의 기능을 결합하여 보다 효과적인 성능을 달성합니다15. 이러한 접근 방식 중 반 능동 제어는 낮은 에너지 소비와 높은 효율의 균형으로 인해 특히 유망한 것으로 간주됩니다16 , 17 , 18 . 우수한 동적 댐핑 특성을 가진 자기 유변학(MR) 댐퍼는 가장 효과적인 반능동 제어 장치 중 하나로 간주됩니다 19,20,21,22.
그러나 MR 댐퍼를 사용하는 반능동 제어 시스템에서는 피드백 로직이 불가피하게 시간 지연을 유발하기 때문에 문제가 발생합니다. 이러한 지연은 전형적으로 다음과 같은 몇 가지 요인(23,24,25)에 의해 발생한다: (i) 센서 데이터의 획득 및 처리, (ii) 제어기(26)에 의한 요구되는 제어력의 계산, (iii) 트랜스듀서를 통한 MR 댐퍼(27)로의 신호 전송, 및 (iv) MR 댐퍼 자체에 의한 실제 힘 생성(28). 이러한 시간 지연은 생성된 제어력과 구조물에 의해 예상되는 힘 사이의 불일치를 초래할 수 있으며, 이는 제어 효과(29)를 크게 손상시킬 수 있다. 불행히도 MR 댐퍼에 대한 대부분의 기존 제어 알고리즘은 이러한 지연을 고려하지 않습니다.
또한 재앙적 사건의 고유한 임의성으로 인해 효과적인 반능동 제어 알고리즘은 확률적 여기(stochastic excitations)에서 성능을 유지할 수 있어야 합니다. MR 댐퍼가 장착된 구조물의 진동을 완화하기 위해 고전적인 확률적 최적화 기법인 LQG(Linear Quadratic Gaussian) 제어 방법이 연구되었습니다. 예를 들어, Dyke 등은 가속도 피드백30을 사용하여 MR 댐퍼가 장착된 구조물의 지진 응답을 개선하기 위한 LQG 클리핑 최적 제어 전략을 제안했습니다. Ying et al.은 확률적 평균화 및 동적 프로그래밍 기술을 통합하여 MR 댐퍼가 있는 비선형 구조에 대한 비클리핑 반능동 확률적 최적 제어 전략을 도입했습니다31. 다른 연구에서는 기지 격리 건물(19)의 내진 성능을 향상시키기 위해 모달 기반 LQG 제어를 적용하고 풍력 터빈 타워(32)의 진동 완화에 대한 효과를 분석했습니다. 그러나 백색 가우스 잡음을 가정하는 고전적인 LQG 방법은 지진이나 강풍과 같은 실제 가진의 비정상, 비가우스 특성을 모델링하는 데 적합하지 않습니다. 이를 해결하기 위해 물리적 기반 확률적 최적(PSO) 제어의 개념이 개발되었습니다33,34 이는 기존 LQG 방법의 한계를 극복하고 다양한 확률적 여기를 처리하기 위한 보다 정확한 프레임워크를 제공합니다35. 연구에 따르면 PSO 기반 반능동 확률적 최적 제어는 확률적 지진력36의 영향을 받는 선형 및 비선형 구조 모두에 대한 진동 완화를 크게 향상시킵니다.
따라서, 시간 지연을 보상하는 강력한 반능동 제어 방법에 대한 시급한 요구가 있으며, MR 댐퍼에 의해 제어되는 구조의 신뢰성을 향상시킨다25,37. 또한, 확률적 여기(stochastic excitation)에서 최적의 제어 성능을 보장하려면 신뢰성 기반 접근 방식을 사용하여 제안된 제어 방법의 중요 매개변수를 최적화하는 것이 필수적입니다. 따라서 본 논문에서는 MR 댐퍼가 있는 구조물의 신뢰성을 향상시키기 위해 SOSC-PSO(Time Delay Compensation)를 이용한 확률적 최적 반능동 제어 방법을 제안합니다.
프로토콜
1. 확률적 최적 반능동 제어 방식
MR 댐퍼의 제어 효과는 불가피한 시간 지연에 의해 큰 영향을 받기 때문에 제어 구조물의 성능을 높이기 위해 시간 지연 보상 알고리즘을 사용한 반능동 제어 방법이 개발됩니다. 게다가, 외부 흥분에 내재된 무작위성은 동적 반응의 명백한 불확실성을 야기합니다. PSO 제어는 구조 제어 시스템의 신뢰성을 보장하기 위해 제안된 방법의 중요한 매개변수를 최적화하기 위해 도입되었습니다.
1.1 semi-active control의 보상 알고리즘
일반성을 잃지 않고 시간 지연이 있는 MR 댐퍼에 의해 제어되는 n-DOF(n-Degree-Of-Freedoms) 구조를 고려하면 확률적 가진에 영향을 받는 모션 방정식은 다음과 같이 주어집니다.
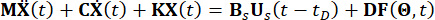 (1)
(1)
여기서  는 각각 구조의 n x n 질량, 감쇠 및 강성 행렬을 나타내고, n은 제어되는 구조의 자유도 수를 나타냅니다. 구조체의 변위, 속도 및 가속도 벡터는 각각 로 표시됩니다
는 각각 구조의 n x n 질량, 감쇠 및 강성 행렬을 나타내고, n은 제어되는 구조의 자유도 수를 나타냅니다. 구조체의 변위, 속도 및 가속도 벡터는 각각 로 표시됩니다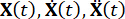 . 기호 위의 작은 1과 2개의 점은 첫 번째 및 두 번째 도함수를 나타냅니다. U, s(t -t, D)는 MR 댐퍼의 시간 지연 제어력의 r차원 벡터를 나타내고, r은 댐퍼의 수를 나타냅니다. t는 시간을 나타냅니다. t D 는 이 연구에서 모든 댐퍼에서 균일하다고 가정되는 시간 지연을 의미하며,
. 기호 위의 작은 1과 2개의 점은 첫 번째 및 두 번째 도함수를 나타냅니다. U, s(t -t, D)는 MR 댐퍼의 시간 지연 제어력의 r차원 벡터를 나타내고, r은 댐퍼의 수를 나타냅니다. t는 시간을 나타냅니다. t D 는 이 연구에서 모든 댐퍼에서 균일하다고 가정되는 시간 지연을 의미하며, 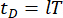 여기서 는 정수
여기서 는 정수 
 이고 샘플링 기간을 나타냅니다.
이고 샘플링 기간을 나타냅니다. 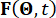 는 확률적 여기(stochastic excitations)의 p차원 벡터를 나타내고
는 확률적 여기(stochastic excitations)의 p차원 벡터를 나타내고 , 외부 여기(external excitations)와 관련된 임의성을 특성화하는 확률적 매개변수 벡터를 나타냅니다. 의
, 외부 여기(external excitations)와 관련된 임의성을 특성화하는 확률적 매개변수 벡터를 나타냅니다. 의  치수는 외부 가진에 사용되는 모델에 따라 다르지만 구조의 기계적 자유도와는 관련이 없습니다. B, s, D는 각각 댐퍼와 외부 가진의 위치를 지정하는 n x r 행렬과 n x p 행렬입니다. 상태공간 표현에서 식 (1)은 다음과 같이 작성됩니다.
치수는 외부 가진에 사용되는 모델에 따라 다르지만 구조의 기계적 자유도와는 관련이 없습니다. B, s, D는 각각 댐퍼와 외부 가진의 위치를 지정하는 n x r 행렬과 n x p 행렬입니다. 상태공간 표현에서 식 (1)은 다음과 같이 작성됩니다.
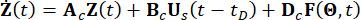 (2)
(2)
여기서 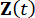 , 는 2n차원 상태 벡터를 나타내고,
, 는 2n차원 상태 벡터를 나타내고, 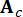 는 2n x 2n 시스템 매트릭스를 나타내며,
는 2n x 2n 시스템 매트릭스를 나타내며, 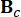 MR 댐퍼의 2n x r 위치 매트릭스를 나타내고;
MR 댐퍼의 2n x r 위치 매트릭스를 나타내고; 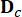 외부 여기의 2N x P 위치 매트릭스를 나타냅니다. 이러한 매개변수는 다음과 같이 표현됩니다.
외부 여기의 2N x P 위치 매트릭스를 나타냅니다. 이러한 매개변수는 다음과 같이 표현됩니다.
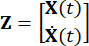 ,
, 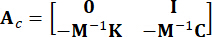 ,
, 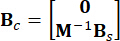 ,
, 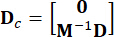 (3)
(3)
여기서  는 와 같은 순서를
는 와 같은 순서를 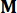 가진 항등 행렬을 나타냅니다. 계산의 편의를 위해 연속 상태 공간 방정식 식 (2)는 다음과 같이 이산 형식으로 표현될 수 있습니다.
가진 항등 행렬을 나타냅니다. 계산의 편의를 위해 연속 상태 공간 방정식 식 (2)는 다음과 같이 이산 형식으로 표현될 수 있습니다.
 (4)
(4)
여기서 시점  은 로 단순화
은 로 단순화 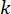 됩니다. 그리고
됩니다. 그리고  ,
, 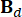 는
는 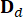 2n x 2n, 2n x r 및 2n x p 행렬을 나타내며 다음과 같이 표현됩니다.
2n x 2n, 2n x r 및 2n x p 행렬을 나타내며 다음과 같이 표현됩니다.
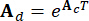 ,
, 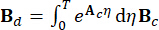 ,
, 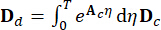 (5)
(5)
여기서 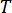 는 샘플링 기간을 나타냅니다.
는 샘플링 기간을 나타냅니다.
능동 제어와 유사한 효과를 달성하기 위해 시간 지연이 있는 MR 댐퍼 기반 제어에 대해 Hrovat 알고리즘38을 기반으로 하는 간단하고 효율적인 제어 방법이 제안됩니다.
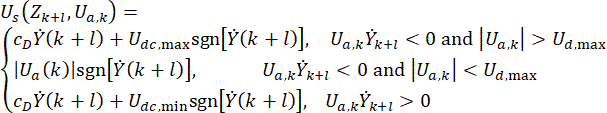 (6)
(6)
여기서 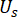 는 MR 댐퍼에 대한 시점\
는 MR 댐퍼에 대한 시점\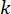 에서의 반능동 제어력 신호를 나타냅니다.
에서의 반능동 제어력 신호를 나타냅니다. 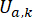 시간 지연 보상이 있는 기준 능동 제어력을 나타냅니다.
시간 지연 보상이 있는 기준 능동 제어력을 나타냅니다.  는 MR 댐퍼의 최대 감쇠력을 나타내며, 이는 변경 가능합니다.
는 MR 댐퍼의 최대 감쇠력을 나타내며, 이는 변경 가능합니다. 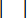 절대값 연산 기호를 나타냅니다.
절대값 연산 기호를 나타냅니다. 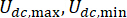 MR 댐퍼의 최대 및 최소 쿨롱 힘을 나타냅니다.
MR 댐퍼의 최대 및 최소 쿨롱 힘을 나타냅니다. 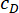 는 점성 감쇠 계수를 나타냅니다.
는 점성 감쇠 계수를 나타냅니다. 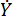 는 MR 댐퍼에 입력된 속도를 나타내며, 이는 댐퍼 실린더에 대한 피스톤의 운동 속도입니다. 식 (6)
는 MR 댐퍼에 입력된 속도를 나타내며, 이는 댐퍼 실린더에 대한 피스톤의 운동 속도입니다. 식 (6) 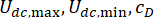 에서 MR 댐퍼의 설계 매개변수를 나타냅니다.
에서 MR 댐퍼의 설계 매개변수를 나타냅니다.
식 (6)은 시간 지연에 따른 MR 댐퍼의 반능동 제어력의 계산을 보여줍니다. 식 (4)의 시간 단계 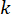 에서의 반능동 제어력
에서의 반능동 제어력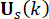 은, 시간 스텝
은, 시간 스텝 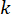 에서의 능동 제어력
에서의 능동 제어력  과 시간 스텝 지연 이후의 시간 스텝
과 시간 스텝 지연 이후의 시간 스텝 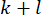 에서의 상태 변수를
에서의 상태 변수를 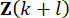 기반으로 계산됨을 알 수
기반으로 계산됨을 알 수 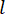 있다. 활동적인 통제력을
있다. 활동적인 통제력을  얻기 위하여는, 전통적인 비용 함수는 곁에 설치됩니다
얻기 위하여는, 전통적인 비용 함수는 곁에 설치됩니다
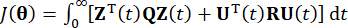 (7)
(7)
여기서  , 는 시스템 상태의 2n x 2n 대칭 양의 준정부호 가중치 행렬을 나타내고,
, 는 시스템 상태의 2n x 2n 대칭 양의 준정부호 가중치 행렬을 나타내고, 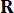 는 제어력의 r x r 대칭 양의 정부호 가중치 행렬을 나타낸다. 외부 흥분은 무시할 수 있는 것으로 보입니다. 실제로, 식 (7)을 기준으로 구조 제어 시스템은 외부 여기의 종류에 관계없이 최적의 제어 효과를 얻을 수 있습니다. 이산 형식으로서, 식 (7)은39로 표현된다.
는 제어력의 r x r 대칭 양의 정부호 가중치 행렬을 나타낸다. 외부 흥분은 무시할 수 있는 것으로 보입니다. 실제로, 식 (7)을 기준으로 구조 제어 시스템은 외부 여기의 종류에 관계없이 최적의 제어 효과를 얻을 수 있습니다. 이산 형식으로서, 식 (7)은39로 표현된다.
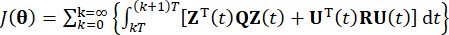 (8)
(8)
비용 함수의  최소화는 조건부 극한 값 문제로 이어지며 활성 제어력
최소화는 조건부 극한 값 문제로 이어지며 활성 제어력 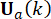 은25로 계산됩니다.
은25로 계산됩니다.
 (9)
(9)
여기서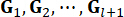 , 는 시간 스텝
, 는 시간 스텝 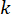 에서의 상태 변수
에서의 상태 변수 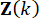 와 시간 스텝
와 시간 스텝 에서의 활성 제어력
에서의 활성 제어력 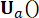 에 대한 제어 이득을 나타내며, 이는 가중 행렬
에 대한 제어 이득을 나타내며, 이는 가중 행렬 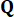 및
및 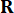 37에 의해 결정된다. 불가피한 시간 지연 이후, 얻어진 제어력
37에 의해 결정된다. 불가피한 시간 지연 이후, 얻어진 제어력  은 시점에서
은 시점에서 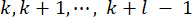 구조물에 작용합니다. 따라서 식 (9)의 활성 제어력은 다음과 같이 계산됩니다.
구조물에 작용합니다. 따라서 식 (9)의 활성 제어력은 다음과 같이 계산됩니다.
 (10)
(10)
개념의 명확성을 위해, 식 (10)의 반능동 제어력은 식 (6)을 기준으로 다음과 같이 표현됩니다.
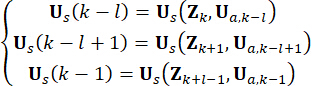 (11)
(11)
여기서 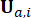 는 시점
는 시점  에서의 활성 제어력을 나타냅니다. 식 (11)을 식 (10)으로 대입하고,
에서의 활성 제어력을 나타냅니다. 식 (11)을 식 (10)으로 대입하고,
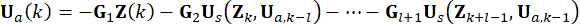 (12)
(12)
참고: 시점 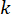 부터 까지의
부터 까지의 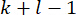 모든 상태
모든 상태  값은 를 계산하는
값은 를 계산하는  데 필요합니다. 따라서, 다음과 같은 상태 예측 방법을 소개한다(40).
데 필요합니다. 따라서, 다음과 같은 상태 예측 방법을 소개한다(40).
 (13)
(13)
여기서  는 예측 변수를 나타냅니다. 식 (13)의 반복에 의해, 의
는 예측 변수를 나타냅니다. 식 (13)의 반복에 의해, 의 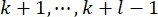 상태가
상태가  계산됩니다. 능동 제어력 Ua(k)는 다음과 같이 표현됩니다.
계산됩니다. 능동 제어력 Ua(k)는 다음과 같이 표현됩니다.
 (14)
(14)
반능동 제어력은 Eqs를 결합하여 얻을 수 있습니다. (6), (12), (13).
1.2 구조 제어 시스템의 신뢰성 분석
확률 보존의 원칙에 따르면, 증강 시스템 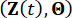 및
및  MR 댐퍼가 있는 구조는 확률이 보존되며, 다음과 같은 일반화된 확률 밀도 진화 방정식(GDEE)38에 의해 제어됩니다.
MR 댐퍼가 있는 구조는 확률이 보존되며, 다음과 같은 일반화된 확률 밀도 진화 방정식(GDEE)38에 의해 제어됩니다.
 (15)
(15)
 (16)
(16)
여기서 , 는
, 는 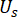 각각 시간 지연을 갖는 시스템 상태 및 반능동 제어력의 해당 성분을 표시하고,
각각 시간 지연을 갖는 시스템 상태 및 반능동 제어력의 해당 성분을 표시하고, 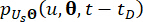
 는 각각 증강된 샘플 시스템의
는 각각 증강된 샘플 시스템의 
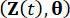 결합 확률 밀도 함수를 표시하고,
결합 확률 밀도 함수를 표시하고,  는 의
는 의  샘플 공간 내의 샘플을 표시하고,
샘플 공간 내의 샘플을 표시하고, 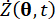 는
는 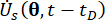 각각 시스템 상태 및 반능동 제어력 구성 요소의 1차 시간 편도함수를 표시한다. 결합 확률 밀도는 기능
각각 시스템 상태 및 반능동 제어력 구성 요소의 1차 시간 편도함수를 표시한다. 결합 확률 밀도는 기능  하며
하며 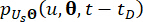 Eqs를 해결하여 달성할 수 있습니다. (15) 및 (16)을 다음과 같은 초기 조건으로 합니다.
Eqs를 해결하여 달성할 수 있습니다. (15) 및 (16)을 다음과 같은 초기 조건으로 합니다.
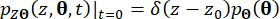 (17)
(17)
 (18)
(18)
여기서  는 Dirac 델타 기능을 나타냅니다.
는 Dirac 델타 기능을 나타냅니다. 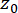
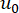 는 각각 와
는 각각 와 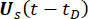 의 결정론적 초기값을
의 결정론적 초기값을 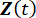 나타내고,
나타내고,  는 sample
는 sample 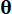 의 확률 밀도 함수를 나타냅니다.
의 확률 밀도 함수를 나타냅니다.
의 순간 확률 밀도 함수는 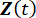
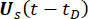 샘플 공간 영역의 1
샘플 공간 영역의 1 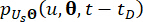 차원 적분
차원 적분  에 의해 얻어질 수 있습니다.
에 의해 얻어질 수 있습니다.
 (19)
(19)
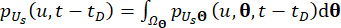 (20)
(20)
여기서 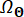 는 의
는 의  분포 영역을 나타냅니다.
분포 영역을 나타냅니다.
Eqs를 기반으로 합니다. (19) 및 (20)에서, 알고리즘 매개변수와 관련된 관계가 정의되는 경우, 관련 물리량의 완전한 확률적 정보가 쉽게 도출되는 것을 볼 수 있습니다. 관련 물리량의 신뢰성은 다음과 같은 관련 성능 함수로 계산할 수 있습니다.
 (21)
(21)
 (22)
(22)
여기서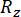 , 는
, 는 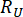 각각
각각 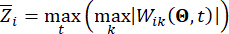 관련 상태량 및 반능동 제어력의 계산된 신뢰도를 표시하고; 는 제어된 구조체의 i번째 관련 물리량의 등가 극값 벡터를 표시하고;
관련 상태량 및 반능동 제어력의 계산된 신뢰도를 표시하고; 는 제어된 구조체의 i번째 관련 물리량의 등가 극값 벡터를 표시하고; 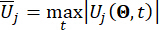 는 j번째 제어력의 등가 극값 벡터를 표시하고; 기호들 상의 모자 '-'는 등가 극값 벡터(41)를 표시하고;
는 j번째 제어력의 등가 극값 벡터를 표시하고; 기호들 상의 모자 '-'는 등가 극값 벡터(41)를 표시하고; 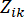 는 제어된 구조의 k번째 DOF의 i번째 관련 물리량을 표시하고;
는 제어된 구조의 k번째 DOF의 i번째 관련 물리량을 표시하고; 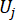 는 j번째 제어력을 표시하고;
는 j번째 제어력을 표시하고; 
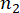
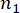
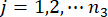
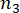 는
는 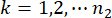 각각 구조체 및 구조체에 설치된 MR 댐퍼의 관련 물리량 및 DOF의 수를 나타낸다.
각각 구조체 및 구조체에 설치된 MR 댐퍼의 관련 물리량 및 DOF의 수를 나타낸다. 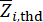 및
및  의
의  임계값
임계값 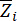 을 표시하고,
을 표시하고,  는 무작위 이벤트의 확률을 의미한다.
는 무작위 이벤트의 확률을 의미한다.
1.3 매개 변수 최적화
의  진폭의 비율은
진폭의 비율은 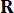 피드백 제어 양식에서 제어 효과(38)에 큰 영향을 미친다. 따라서 최상의 제어 효과를
피드백 제어 양식에서 제어 효과(38)에 큰 영향을 미친다. 따라서 최상의 제어 효과를 달성하고
달성하고 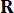 최적화해야 합니다. 또한, MR 댐퍼 기반 제어 방법으로서 제어 효율성은 식 (6)의 장치 매개변수
최적화해야 합니다. 또한, MR 댐퍼 기반 제어 방법으로서 제어 효율성은 식 (6)의 장치 매개변수 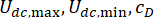 에 의해서도 영향을 받습니다. 구조 제어 시스템의 최적 신뢰성을 달성하기 위해 신뢰성 기반 기준이 식 (25)에서 제안되었습니다.
에 의해서도 영향을 받습니다. 구조 제어 시스템의 최적 신뢰성을 달성하기 위해 신뢰성 기반 기준이 식 (25)에서 제안되었습니다.

그림 1: 시간 지연 보상을 통한 확률적 최적 반능동 구조 제어를 위한 매개변수 최적화의 흐름도. 약어: GDEE = 이벤트의 일반화된 미분 방정식 ; PDF = 확률 밀도 함수. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
요약하면, 시간 지연 보상과 함께 MR 댐퍼를 기반으로 확률적 최적 반능동 구조 제어를 수행하려면 두 단계가 필요합니다.
1.3.1 식 (7)에 나타난 비용 함수를  최소화하면, 샘플의 의미에서 상태 피드백 로직, 즉 식 12)가 달성된다.
최소화하면, 샘플의 의미에서 상태 피드백 로직, 즉 식 12)가 달성된다.
1.3.2 신뢰성 기반 성능 기능을  최소화하여 통계학적 측면에서 최적의 매개변수를 달성합니다. 그림 1은 1.3.2단계에서 컨트롤러 매개변수의 최적화 순서도를 보여줍니다.
최소화하여 통계학적 측면에서 최적의 매개변수를 달성합니다. 그림 1은 1.3.2단계에서 컨트롤러 매개변수의 최적화 순서도를 보여줍니다.
두 개의 루프 계층을 포함하는 1.3.2단계의 다음 단계는 다음과 같습니다.
1.3.2.1 확률적 매개 변수 벡터 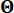 를 특징으로 하는 확률적 여기의 확률 할당 공간을 분할하면 할당된 관련 확률과 함께 대표 점
를 특징으로 하는 확률적 여기의 확률 할당 공간을 분할하면 할당된 관련 확률과 함께 대표 점  집합을 식별할 수 있습니다Pq. 이 접근 방식을 사용하면 로 표시되는
집합을 식별할 수 있습니다Pq. 이 접근 방식을 사용하면 로 표시되는 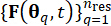 확률적 여기(stochastic excitation)에 대한 샘플 프로세스를 쉽게 생성할 수 있습니다.
확률적 여기(stochastic excitation)에 대한 샘플 프로세스를 쉽게 생성할 수 있습니다.
1.3.2.2 반능동 구조 제어 시스템의 파라미터 최적화를 위해 비용-함수 가중치  및
및 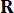 의 값을 초기화하거나 업데이트합니다. 그런 다음 시간 지연과 관련된 상태 피드백 제어력(식 (12 참조))을 계산합니다.
의 값을 초기화하거나 업데이트합니다. 그런 다음 시간 지연과 관련된 상태 피드백 제어력(식 (12 참조))을 계산합니다.
1.3.2.3 Eqs에 표시된 GDEE를 풀어 구조적 반응 및 제어력의 확률 밀도 함수(PDF)를 구합니다. (17)–(20):
최적화는 오프라인 완료이지만 온라인이 아닙니다. 제안된 방법을 실제 구조 제어 시스템에 적용할 수 있는 경우, 최적  및
및 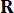 달성이 이루어졌으며, 실제 적용 가능한 프로세스에서는 최적화가 필요하지 않습니다.
달성이 이루어졌으며, 실제 적용 가능한 프로세스에서는 최적화가 필요하지 않습니다.
샘플 여기(sample excitation)를 받는 반능동 구조 제어 시스템의 결정론적 동적 분석으로, 이를 통해 관련 물리량 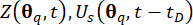 과 그 파생물이
과 그 파생물이  계산됩니다.
계산됩니다.
TVD(Total Variation Diminishing) 속성을 가진 수정된 Lax-Wendroff 기법과 같은 유한 차분법을 사용하여 GDEE(Generalized Differential Equations)를 풀고 결합 확률 밀도 함수에 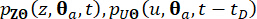 대한 수치 해를 도출할 수 있습니다.
대한 수치 해를 도출할 수 있습니다.
위의 결정론적 동적 분석과 유한 차분 방법의 두 단계를 반복하고 모든 대표점을 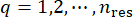 실행하면 합산을 통해 확률 밀도 함수를 얻을 수 있습니다.
실행하면 합산을 통해 확률 밀도 함수를 얻을 수 있습니다.
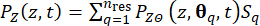 (23)
(23)
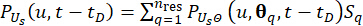 (24)
(24)
여기서 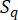 는 샘플 점
는 샘플 점  과 연결된 하위 영역의 면적 측정값을 나타냅니다. GDEE(Generalized Differential Equation of the Event)를 푸는 데 사용되는 방법은 확률 밀도 진화 방법(PDEM)42으로 알려져 있습니다.
과 연결된 하위 영역의 면적 측정값을 나타냅니다. GDEE(Generalized Differential Equation of the Event)를 푸는 데 사용되는 방법은 확률 밀도 진화 방법(PDEM)42으로 알려져 있습니다.
1.3.2.4 관련 물리량의 PDF는 신뢰성을 평가하는 데 사용되며, 이는 확률 기준의 성능 함수에  통합됩니다.
통합됩니다.
1.3.2.5 매개변수 최적화 프로세스에 대한 종료 기준이 충족되었는지 평가합니다. 조건이 충족되지 않으면 1.3.2.2단계로 돌아갑니다. 그렇다면 시간 지연 제어 시스템에 대한 최적의 매개변수를 결정할 수 있습니다. 이 작업에서는 MATLAB의 유전 알고리즘(GA) 툴박스가 파라미터 최적화에 사용되어 파라미터 업데이트를 용이하게 하고 종료 조건을 정의합니다. 유전 알고리즘을 통해 10번의 반복 이내에 최적의 값을 얻을 수 있으며 수렴은 국소 최소값 문제 없이 안정적입니다. GA의 계산 비용은 입자 군집 최적화나 그래디언트 기반 방법보다 크지만, GA는 이 원고에 있는 것과 같이 복잡하고 미분화할 수 없는 문제를 처리하는 데 적합합니다. 따라서 GA가 적용됩니다. 그리고 빠른 수렴 속성 때문에 GA의 계산 비용이 허용됩니다.
1.3.2.6 최적의 신뢰성 제어를 달성하기 위해 다음과 같은 성능 함수를  공식화합니다. 매개변수
공식화합니다. 매개변수 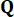 의 최적 값을 결정하기 위해 최소화
의 최적 값을 결정하기 위해 최소화  하고
하고  다음을 수행합니다.
다음을 수행합니다.
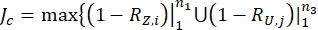 } (25)
} (25)
 (26)
(26)
앞서 언급했듯이 컨트롤러의 가중치 매트릭스는 대칭이며, 여기서 matrix 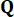 의 요소는 변위, 속도 및 상호 작용에 할당된 가중치에 해당하고 matrix
의 요소는 변위, 속도 및 상호 작용에 할당된 가중치에 해당하고 matrix  의 요소는 제어력과 관련된 가중치를 나타냅니다. 이전 연구의 결과에 기초하여38, 비용-함수 가중치
의 요소는 제어력과 관련된 가중치를 나타냅니다. 이전 연구의 결과에 기초하여38, 비용-함수 가중치 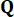 의 구성을 다양화하고
의 구성을 다양화하고  제어 효과에 미치는 영향이 최소화되는 것이 관찰되었습니다. 결과적으로, 이 연구에서는 다음과 같이 단순화된 구성이 채택되었습니다.
제어 효과에 미치는 영향이 최소화되는 것이 관찰되었습니다. 결과적으로, 이 연구에서는 다음과 같이 단순화된 구성이 채택되었습니다.
 ,
,  (27)
(27)
여기서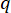 , 는 정의될 상태 가중치 매트릭스의 계수를 나타내고, 는 정의될 제어 가중치 매트릭스의 계수를 나타내고,
, 는 정의될 상태 가중치 매트릭스의 계수를 나타내고, 는 정의될 제어 가중치 매트릭스의 계수를 나타내고, 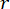
 는 항등 행렬을 나타냅니다. 제어 효과는 의
는 항등 행렬을 나타냅니다. 제어 효과는 의 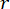 비율
비율 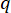 에 의해 영향을 받지만 값 자체에 의해 영향을 받지는 않습니다. 또한,
에 의해 영향을 받지만 값 자체에 의해 영향을 받지는 않습니다. 또한,  식 (6)은 MR 댐퍼의 최소 쿨롱 힘을 나타내며, 이는 댐퍼의 전류 입력이 0임을 의미합니다
식 (6)은 MR 댐퍼의 최소 쿨롱 힘을 나타내며, 이는 댐퍼의 전류 입력이 0임을 의미합니다 . 그러면, 식 (26)은 다음과 같이 더 표현될 수 있습니다.
. 그러면, 식 (26)은 다음과 같이 더 표현될 수 있습니다.
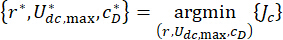 (28세)
(28세)
최적의 관심 계수는 어디에 있습니까 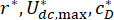 ? 엔지니어링에서 합리적으로 만들기 위해 최적의 범위는 MR 댐퍼 공장의 생산 능력을 기반으로 합니다.
? 엔지니어링에서 합리적으로 만들기 위해 최적의 범위는 MR 댐퍼 공장의 생산 능력을 기반으로 합니다.
분명히, 식 (28)에 의해 얻어진 최적 매개변수는 시간 지연과 함께 제안된 반능동 제어 알고리즘의 최적 제어 효율성을 유지하며, 이는 구조 제어 시스템이 확률적 여기(stochastic excitations)에 종속된 균형 잡힌 최적 신뢰성을 달성할 수 있도록 합니다.
2. 사례 연구
MR 댐퍼에 대한 시간 지연 보상과 함께 제안된 반능동 제어 방법의 효과를 분석하기 위해 MR 댐퍼에 부착된 평면 단층 전단 프레임 구조를 그림 2와 같이 수평 확률적 지진 지반 운동을 적용했습니다. 반 능동적으로 통제되는 구조 체계의 모수는 다음과 같이 입니다: 구조 질량 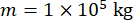 , 자연적인 원형 주파수
, 자연적인 원형 주파수 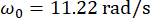 , 감쇠 비율
, 감쇠 비율 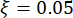 . 과거의 경험과 시장의 기존 댐퍼 스케일에 따르면 구조적 변위, 속도, 가속도 및 제어력의 임계값은 각각 10mm, 100mm/s, 1,500mm/s2 및 150kN입니다. 확률적 지진 지반 운동을 표현하기 위해, 물리적으로 동기 부여된 확률적 지반 운동 모델이 사용되었다43:
. 과거의 경험과 시장의 기존 댐퍼 스케일에 따르면 구조적 변위, 속도, 가속도 및 제어력의 임계값은 각각 10mm, 100mm/s, 1,500mm/s2 및 150kN입니다. 확률적 지진 지반 운동을 표현하기 위해, 물리적으로 동기 부여된 확률적 지반 운동 모델이 사용되었다43:
 (29세)
(29세)
여기서 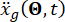 는 엔지니어링 현장의 시간 영역에서의 지면 운동을 나타내고
는 엔지니어링 현장의 시간 영역에서의 지면 운동을 나타내고 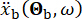 , 기반암의 주파수 영역에서의 지면 운동을 나타냅니다. 이 벡터
, 기반암의 주파수 영역에서의 지면 운동을 나타냅니다. 이 벡터 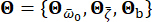 는 엔지니어링 현장 표면에서 지면 운동의 확률적 특성을 나타냅니다. 매개변수는
는 엔지니어링 현장 표면에서 지면 운동의 확률적 특성을 나타냅니다. 매개변수는 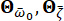 우세한 빈도
우세한 빈도 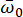 와 등가 댐핑
와 등가 댐핑 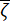 을 포함하여 현장 토양의 특성을 설명하는 확률적 변수입니다. 벡터
을 포함하여 현장 토양의 특성을 설명하는 확률적 변수입니다. 벡터 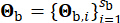 는 기반암에서 지면 운동의 확률적 특성을 나타내며, 이는 소스 속성과 전파 경로
는 기반암에서 지면 운동의 확률적 특성을 나타내며, 이는 소스 속성과 전파 경로 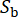 의 영향을 받으며 이 단계에서 관련된 확률적 변수의 수를 나타냅니다.
의 영향을 받으며 이 단계에서 관련된 확률적 변수의 수를 나타냅니다. 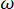 는 원형 주파수를 나타내고 i는 허수 단위입니다.
는 원형 주파수를 나타내고 i는 허수 단위입니다.
엔지니어링 현장의 우세한 주파수  와 등가 감쇠비
와 등가 감쇠비 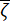 는 현장 토양의 동적 특성을 특징짓는 핵심 매개변수입니다. 이러한 수량의 확률 분포 및 통계적 매개변수는 특정 등급의 엔지니어링 현장에서 수집된 지진 가속도 기록을 기반으로 결정될 수 있습니다. 설명을 위해 전단파 속도 범위가 [150, 250] m/s인 사이트 클래스를 고려하고 지면 운동의 설계 특성 기간을 0.45초로 설정했습니다.
는 현장 토양의 동적 특성을 특징짓는 핵심 매개변수입니다. 이러한 수량의 확률 분포 및 통계적 매개변수는 특정 등급의 엔지니어링 현장에서 수집된 지진 가속도 기록을 기반으로 결정될 수 있습니다. 설명을 위해 전단파 속도 범위가 [150, 250] m/s인 사이트 클래스를 고려하고 지면 운동의 설계 특성 기간을 0.45초로 설정했습니다.
임계 매개변수  는
는 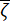 상호 독립적인 확률 변수로 처리되었으며, 둘 다 매개변수 식별을 위한 로그-정규 분포를 따랐습니다. 통계적 매개변수는 다음과 같습니다: 의
상호 독립적인 확률 변수로 처리되었으며, 둘 다 매개변수 식별을 위한 로그-정규 분포를 따랐습니다. 통계적 매개변수는 다음과 같습니다: 의 
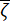 평균은 각각 12 rad/s 및 0.1이었습니다. 의
평균은 각각 12 rad/s 및 0.1이었습니다. 의 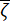 변동
변동  계수는 각각 0.42와 0.35였습니다. 기반암에서의 지반 운동은 0.11g의 피크 지반 가속도에 해당하는 0.20m/s2의 푸리에 진폭을 가진 가우스 백색 잡음 프로세스로 모델링되었습니다. 기반암 운동을 생성하는 데 사용된 위상각은 로
계수는 각각 0.42와 0.35였습니다. 기반암에서의 지반 운동은 0.11g의 피크 지반 가속도에 해당하는 0.20m/s2의 푸리에 진폭을 가진 가우스 백색 잡음 프로세스로 모델링되었습니다. 기반암 운동을 생성하는 데 사용된 위상각은 로 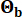 표시되었습니다. 따라서 Sb =1 및
표시되었습니다. 따라서 Sb =1 및 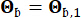 . 이 접근법은 주어진 초과 확률44로 조건부 확률적 지면 운동을 모델링하는 것으로 간주될 수 있습니다. 로그-정규 분포의 가정은 관찰된 지상 운동 매개변수의 왜곡된 특성을 캡처할 수 있는 기능 때문에 지상 모션 모델링에 널리 사용됩니다.
. 이 접근법은 주어진 초과 확률44로 조건부 확률적 지면 운동을 모델링하는 것으로 간주될 수 있습니다. 로그-정규 분포의 가정은 관찰된 지상 운동 매개변수의 왜곡된 특성을 캡처할 수 있는 기능 때문에 지상 모션 모델링에 널리 사용됩니다.
이 가정의 민감도를 평가하기 위해 정규 분포와 감마 분포를 포함한 대안 확률 분포를 사용한 추가 분석이 다른 연구에서 수행되었습니다45,46. 연구 결과에 따르면 전반적인 추세는 일관되게 유지되지만 로그 정규 분포는 특히 지면 운동 강도 측정의 꼬리 동작을 캡처하는 데 관찰된 데이터에 가장 적합함을 나타냅니다
접선 구체 방법(47)에 의해, 관련된 할당된 확률을 가진 221개의 대표 점의 집합이 선택되고 대표적인 지면 가속도가 합성되었습니다. 샘플링 주파수는 50Hz였고 지면 운동의 지속 시간은 20.48초였습니다. 시뮬레이션된 지면 운동에 비정지 강도를 할당하기 위해 균일 변조 기능이 사용되었으며 그 공식은 다음과 같습니다42:
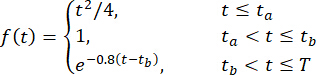 (30세)
(30세)
여기서 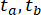 각각 2초와 16초가 걸립니다.
각각 2초와 16초가 걸립니다.
확률적 지진 지반 운동의 평균 및 표준 편차, 그리고 대표적인 지진 지반 운동의 시간 이력이 그림 3에 나와 있습니다. 평균의 진폭(0.06m/s2)은 표준 편차(0.8m/s2)의 진폭의 ~8%였으며, 이는 물리적으로 동기 부여된 확률적 지면 운동 모델이 0 평균의 속성을 나타냈음을 나타냅니다. 한편, 지진파 지반 운동은 시간 영역과 주파수 영역 모두에서 놀라운 비정지 행동을 보였습니다.
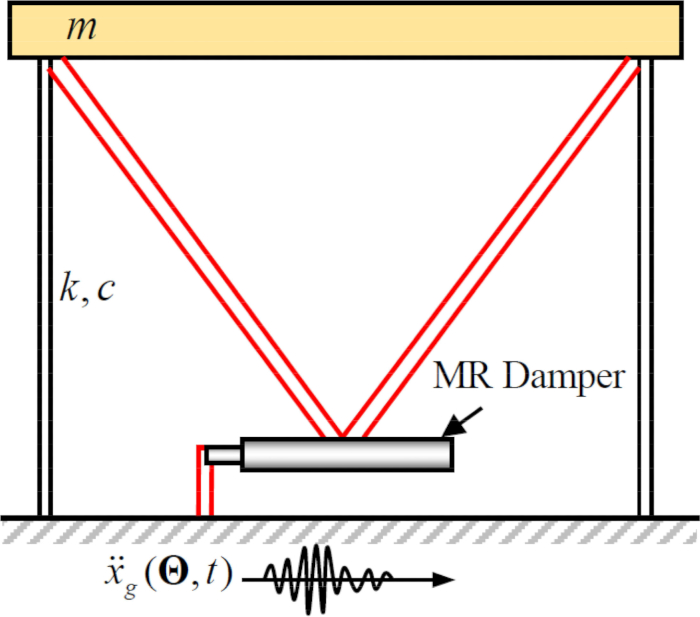
그림 2: 자기유변학적 댐퍼가 있는 단층 전단 프레임의 스케치.  구조 질량, 감쇠비 및 강성을 나타냅니다.
구조 질량, 감쇠비 및 강성을 나타냅니다.  확률적 지진 여기를 나타냅니다. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
확률적 지진 여기를 나타냅니다. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
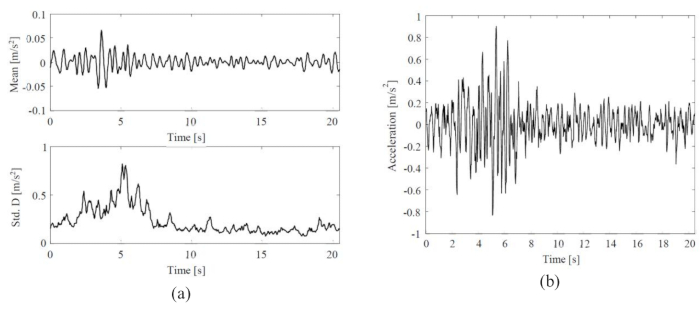
그림 3: 선택된 지진 지반 운동의 통계 및 대표 샘플. (A) 확률적 지진 지반 운동의 평균 및 표준 편차; (B) 대표적인 지진 지반 운동의 시간 이력. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
2.1 시간 지연의 영향 분석
MR 댐퍼의 반능동 제어 효과에 대한 시간 지연의 영향을 분석하기 위해 그림 4 는 제어된 구조의 변위, 속도 및 가속도 RMS(제곱 평균 응답)를 보여줍니다. 가중치 매트릭스 비율 및 댐퍼 파라미터는 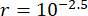 ,
, 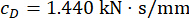 , 및
, 및 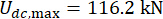 였으며, 이는 시간 지연 없이 최적화된 결과이다(38). 시간 지연에 대한 통제된 구조의 반응은 시간 지연이 없는 통제된 구조물보다 컸으며, 제어 효과에 대한 시간 지연의 영향은 시간 지연의 증가와 함께 주기성을 나타냈습니다. MR 댐퍼를 이용한 반능동 제어 방법은 일종의 피드백 방법이기 때문에 영향의 주기성은 제어 구조의 자연 주기(T = 0.56초)와 관련이 있는 것으로 간주되었습니다.
였으며, 이는 시간 지연 없이 최적화된 결과이다(38). 시간 지연에 대한 통제된 구조의 반응은 시간 지연이 없는 통제된 구조물보다 컸으며, 제어 효과에 대한 시간 지연의 영향은 시간 지연의 증가와 함께 주기성을 나타냈습니다. MR 댐퍼를 이용한 반능동 제어 방법은 일종의 피드백 방법이기 때문에 영향의 주기성은 제어 구조의 자연 주기(T = 0.56초)와 관련이 있는 것으로 간주되었습니다.
최대 MRS 변위, 속도 및 가속도가 24.6mm, 270.0mm/s, 3111.3mm/s2인 비제어 구조의 응답과 비교하여 MR 댐퍼 제어 구조는 주목할만한 효과를 달성했습니다. 시간 지연(time delay)25을 동반한 능동 제어 구조물의 불안정성과 달리, MR 댐퍼 기반 반능동 제어 방법은 시간 지연이 있어도 여전히 약간의 효과를 얻었다.

그림 4: 시간에 따른 제어된 구조체의 응답의 최대 제곱평균 제곱근. (a) 변위; (b) 속도; (C) 가속도. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
반능동적으로 제어되는 구조의 신뢰성에 대한 시간 지연의 영향을 분석하기 위해 그림 5 는 시간 지연이 증가함에 따라 변위, 속도 및 가속도의 신뢰성을 보여줍니다. 시간 지연에 따른 제어된 구조 응답의 신뢰성은 시간 지연이 없는 값보다 낮았으며, 이는 제어된 구조의 신뢰성이 시간 지연에 의해 감소했음을 의미합니다. 한편, 최대 RMS와 유사하게 신뢰성 제어 효과는 시간 지연이 증가함에 따라 주기성을 보였다. 또한, 시간 지연이 있거나 없는 통제된 구조물의 신뢰성은 변위, 속도 및 가속도의 신뢰성이 0.0954, 0.1058 및 0.1111인 통제되지 않은 구조물의 값보다 높았습니다.
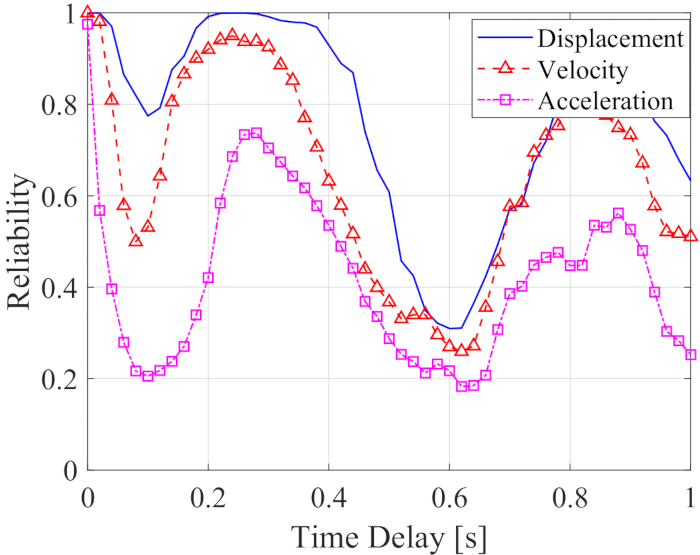
그림 5: 시간 지연이 증가함에 따라 제어된 구조에 대한 응답의 신뢰성. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
요약하면, 구조체의 반응은 반능동 제어 방법에 의해 완화되었습니다. 그러나, RMS 또는 신뢰성에 관계없이 semi-active control 방법의 제어 효율성은 시간 지연에 의해 감소되었습니다. 따라서 시간 지연을 보상해야 합니다.
2.1.1 시간 지연 보상 방법 분석
제안된 시간 지연 보상 방법의 효과를 분석하기 위해 시간 지연이 0.1초인 그림 6에서 제어되지 않는(Unc), 비보상 제어가 있는 시간 지연 시스템(TDN-SAC-PSO) 및 보상 제어가 있는 시간 지연 시스템(TDC-SAC-PSO)에 대한 변위, 속도 및 가속도의 RMS 시간 기록을 비교합니다. 가중치 행렬과 반능동 제어 방법의 매개변수는 2.1단계와 동일합니다.

그림 6: 서로 다른 방법으로 제어되는 구조체의 제곱근-평균-제곱근 시간 이력 비교. (a) 변위; (b) 속도; (c) 가속도; (D) 통제력. 약어: Unc = 통제되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; TDN -SAC-PSO = 비보상이 제어되는 시간 지연 시스템. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
두 가지 제어 방법 모두 제어되지 않은 구조에 비해 구조의 응답을 크게 감소시켜 MR 댐퍼 기반 제어 방법의 장점을 드러냈습니다. TDN-SAC-PSO 방식은 제어되지 않는 구조물과 비교하여 변위, 속도 및 가속도의 최대 RMS가 75.79%, 73.75%, 61.22% 감소합니다. 또한, 시간 지연 보상으로 TDC-SAC-PSO 방법으로 제어된 구조의 응답이 82.59%, 80.40% 및 73.04% 감소합니다. TDC-SAC-PSO 방식의 제어력의 최대 RMS는 TDN-SAC-PSO 방식에 비해 8.43% 감소했지만, 전자의 진동 응답은 후자보다 낮았다. 상술한 분석은 MR 댐퍼 기반 제어 방식에 대한 시간 지연의 영향이 보상 방식에 의해 효과적으로 감소되었음을 나타내며, 이는 MR 댐퍼 반능동 제어 방식에 대한 시간 지연 보상의 필요성을 보여준다.

그림 7: 일반적인 구조 응답 시간에서의 PDF 비교. (a) 변위; (b) 속도; (C) 가속도. 약어: PDF = 확률 밀도 함수; Unc = 제어되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; TDN -SAC-PSO = 비보상이 제어되는 시간 지연 시스템. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
제안된 보상 방법이 제어된 구조의 응답 불확실성에 미치는 영향을 종합적으로 밝히기 위해 일반적인 시간인 3, 7 및 11초에서 변위, 속도 및 가속도의 확률 밀도 함수(PDF) 비교가 그림 7에 나와 있습니다. TDN-SAC-PSO 방법에 대한 PDF는 제어되지 않은 구조체의 PDF보다 좁았는데, 이는 시간 지연이 있더라도 반능동적 제어 방법에 의해 구조 응답의 불확실성이 감소했음을 의미합니다. 시간 지연이 보정되었을 때 응답의 PDF는 더욱 좁아졌습니다. 따라서, 제안된 보상 방법은 semi-active control effect를 향상시키기 위해 필요하다.
| 제어 방법 | 변위 | 속도 | 가속도 | 제어력 | 최소값 |
| 유엔 | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
표 1: 다양한 방법으로 제어되는 구조물의 진동 반응 및 제어력 신뢰성. 약어: Unc = 통제되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; TDN -SAC-PSO = 비보상이 제어되는 시간 지연 시스템.
비제어, TDC-SAC-PSO- 및 TDN-SAC-PSO 방법 제어 구조의 진동 응답 및 제어력 신뢰성은 표 1에 나와 있습니다. TDN-SAC-PSO 방식 제어를 통해 비제어 구조에 비해 구조의 신뢰성이 크게 향상되었으며, 이는 시간이 지남에 따라 MR 댐퍼 기반 제어 방법의 효과를 입증합니다. 그러나 시간 지연 보상으로 인해 특히 가속에 대해 보상이 없는 경우에 비해 신뢰성이 크게 향상되었습니다. 또한 TDC-SAC-PSO 방법에서 서로 다른 반응과 제어력의 신뢰성이 상당한 차이를 보였다는 점도 주목할 만합니다. 이는 시간 지연이 없는 제어에 대한 중요 매개변수의 최적 값이 시간 지연이 있는 제어에 최적이 아님을 나타냅니다. 시간 지연 영향으로 진동 응답과 제어력의 최적 제어 효과를 얻으려면 매개변수를 더욱 최적화해야 합니다. 위의 분석을 바탕으로 MR 댐퍼를 사용한 반능동 제어 방법은 구조물의 진동 응답을 효과적으로 감소시킬 수 있는 반면, 시간 지연의 영향으로 인해 매개변수를 최적화해야 한다는 결론을 내렸습니다.
2.2 매개변수 최적화
파라미터의 최적 값을 달성하기 위해, 신뢰도 기준(reliability criterion)에 기초한 통합 최적화 방법이 적용되었다(38). 임계 매개변수의 최적화는 , 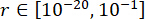 ,
, 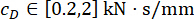
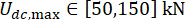 , 및 MR 댐퍼 힘 s = 8의 조정 가능한 시간으로 수행
, 및 MR 댐퍼 힘 s = 8의 조정 가능한 시간으로 수행 되었습니다. 최적화를 구현하기 위해 MATLAB 내의 GA 툴박스가 사용되었습니다.
되었습니다. 최적화를 구현하기 위해 MATLAB 내의 GA 툴박스가 사용되었습니다.
매개변수 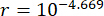 의 최적화 결과는 ,
의 최적화 결과는 , 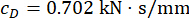 , 및
, 및  시간 지연
시간 지연  에 대한 입니다. 그림 8 은 비제어(Unc), TDC-SAC-PSO 방법 및 SOSC-PSO 방법 제어 구조에 대한 변위, 속도, 가속도 및 제어력의 RMS 시간 기록을 보여줍니다. SOSC-PSO 방법은 시간 지연 보상 및 최적화된 임계 매개변수 값을 사용하는 반능동 제어 방법을 나타냅니다.
에 대한 입니다. 그림 8 은 비제어(Unc), TDC-SAC-PSO 방법 및 SOSC-PSO 방법 제어 구조에 대한 변위, 속도, 가속도 및 제어력의 RMS 시간 기록을 보여줍니다. SOSC-PSO 방법은 시간 지연 보상 및 최적화된 임계 매개변수 값을 사용하는 반능동 제어 방법을 나타냅니다.

그림 8: 비제어 및 TDC-SAC-PSO 방법 및 SOSC-PSO 방법 제어 구조에 대한 변위, 속도, 가속도 및 제어력의 RMS 시간 이력. (a) 변위; (b) 속도; (c) 가속도; (D) 통제력. 약어: Unc = 통제되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; SOSC-PSO = 시간 지연 보상을 사용하는 확률적 최적 반능동 제어 방법. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
도 8에서, TDC-SAC-PSO 및 SOSC-PSO 방법의 제어 효과는 거의 차이를 보이지 않았음을 알 수 있다. 전자의 방법에 대한 변위 속도 및 가속도의 최대 RMS는 제어되지 않은 구조의 81.60%, 81.21%, 73.62%였고 후자의 경우 82.59%, 80.40%, 73.04%였습니다. 두 제어 방법에 대한 응답의 확률 특성을 종합적으로 분석하기 위해 그림 9는 제어되지 않은 TDC-SAC-PSO 방법 및 SOSC-PSO 방법 제어 구조에 대한 변위, 속도 및 가속도의 PDF를 보여줍니다. 두 제어 방법 모두 일반적인 시간에 거의 동일한 변위 및 속도의 PDF를 가졌습니다. SOSC-PSO 방법의 가속도 PDF는 TDC-SAC-PSO 방법의 가속도 PDF보다 좁았으며, 이는 가속의 불확실성이 이전 방법에 의해 더 나은 제어 효과를 달성했음을 의미합니다.
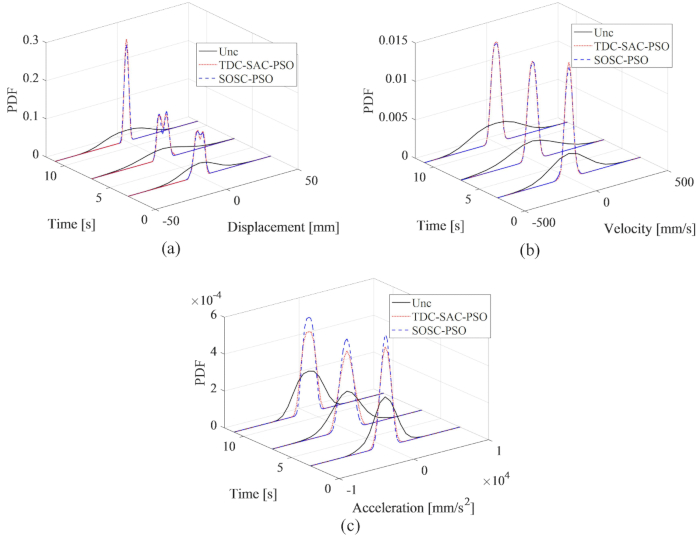
그림 9: 서로 다른 제어 구조물에 대한 변위, 속도 및 가속도에 대한 PDF 비교. (a) 변위; (b) 속도; (C) 가속도. 약어: PDF = 확률 밀도 함수; Unc = 제어되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; SOSC-PSO = 시간 지연 보상을 사용하는 확률적 최적 반능동 제어 방법. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
제어되지 않는 TDC-SAC-PSO- 및 SOSC-PSO 방법 제어 구조에 대한 변위, 속도, 가속도 및 제어력의 신뢰성은 표 2에 나와 있습니다. 두 가지 제어 방법 모두 제어되지 않은 구조에 비해 신뢰성이 크게 향상되었습니다. 변위 신뢰성은 TDC-SAC-PSO 방법과 SOSC-PSO 방법 간에 거의 차이를 보이지 않았습니다. 통제된 구조의 가장 낮은 신뢰성인 가속 신뢰성은 눈에 띄는 증가를 달성했습니다. 이는 SOSC-PSO 방식이 균형 최적 제어 효과를 달성한다는 것을 의미합니다.
| 제어 방법 | 변위 | 속도 | 가속도 | 제어력 | 최소값 |
| 유엔 | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
표 2: 다양한 방법으로 제어되는 구조물에 대한 신뢰성. 약어: Unc = 통제되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; SOSC-PSO = 시간 지연 보상을 사용하는 확률적 최적 반능동 제어 방법.
시간 지연  에 대한 제안된 SOSC-PSO 방법의 효과를 분석했습니다. 상이한 시간 지연에 대해 제안된 방법을 추가로 검증하기 위해, 표 3 은 시간 지연 범위에
에 대한 제안된 SOSC-PSO 방법의 효과를 분석했습니다. 상이한 시간 지연에 대해 제안된 방법을 추가로 검증하기 위해, 표 3 은 시간 지연 범위에  대한 최적의 파라미터 값과 해당 신뢰성을 보여줍니다.
대한 최적의 파라미터 값과 해당 신뢰성을 보여줍니다.
| tD(초) | 엘제(R*) | CD(kN·s/mm) | Udc, 최대 (kN) | 변위 | 속도 | 가속도 | 제어력 |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| 유엔 | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
표 3: 다양한 시간 지연에 대한 최적의 매개변수 값과 해당 신뢰성 값. 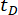 시간 지연을 나타냅니다.
시간 지연을 나타냅니다. 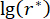 는 r의 최적 로그 값을 나타내고, r은 제어 가중치 매트릭스의 계수를 나타냅니다.
는 r의 최적 로그 값을 나타내고, r은 제어 가중치 매트릭스의 계수를 나타냅니다. 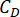 는 MR 댐퍼의 점성 감쇠 계수를 나타냅니다.
는 MR 댐퍼의 점성 감쇠 계수를 나타냅니다. 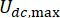 MR 댐퍼의 최대 및 최소 쿨롱 힘을 나타냅니다.
MR 댐퍼의 최대 및 최소 쿨롱 힘을 나타냅니다.
변위, 속도 및 가속도의 신뢰성이 시간 지연이 있는 경우에도 제어되지 않은 구조에 비해 향상되었음을 관찰할 수 있으며, 이는 이러한 지연에 대해 제안된 방법의 견고성을 보여줍니다. 그러나 시간 지연이 증가함에 따라 제안된 제어 방법에 대한 구조적 응답의 신뢰성이 감소했으며, 이는 제어 효과에 대한 시간 지연의 영향을 완화할 수 있지만 완전히 제거할 수는 없음을 나타냅니다. 특히 제어군의 신뢰성은 서로 다른 시간 지연에서 90% 이상을 유지했습니다.
3. 수치 예
MDOF 구조에서 제안된 SOSC-PSO 방법을 검증하기 위해 그림 10과 같이 1층과 3층에 2개의 MR 댐퍼가 설치된 6층 구조를 분석했습니다. 섹션 2의 확률적 지진 모델에 의해 생성된 지진 샘플이 적용되었으며 변위, 속도, 가속도 및 제어력의 신뢰성 임계값은 20mm, 200mm/s, 3,000mm/s2 및 200kN이었습니다. 식. (27)은 와 함께  가중 행렬로 사용되었습니다. MATLAB의 GA 도구 상자는 최적 범위
가중 행렬로 사용되었습니다. MATLAB의 GA 도구 상자는 최적 범위 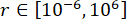 ,
, 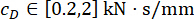 , 및
, 및 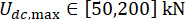 를 사용하여 ,
를 사용하여 ,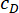 , 및
, 및 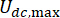 를 최적화하는
를 최적화하는 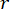 데 사용되었습니다.
데 사용되었습니다.

그림 10: 2개의 MR 댐퍼가 있는 6층 구조. 약어 : MR = magnetorheological. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
3.1 시간 지연의 영향 분석
MDOF 구조에서 MR 댐퍼의 제어 효과에 대한 시간 지연의 영향을 분석하기 위해 그림 11은 TDC-SAC-PSO 방식의 시간 지연과 함께 변위(층간 변위), 속도(층간 속도) 및 가속도(층 가속도)의 최대 RMS를 보여줍니다. 매개변수는 , , 그리고
, 그리고 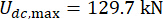 1층의 MR 댐퍼,
1층의 MR 댐퍼,  그리고
그리고 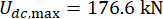 3층의 MR 댐퍼에 대한 것인데
3층의 MR 댐퍼에 대한 것인데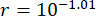 , 이는 시간 지연 없이 최적화된 결과입니다. 제어된 구조 응답의 최대 RMS는 시간 지연과 함께 주기 변동을 나타냈습니다. 변위와 속도의 최대 RMS는 1층에서, 최대 가속도는 6층에서 이루어졌습니다. 또한, 시간 지연이 있는 응답의 모든 최대 MRS는 시간 지연이 없는 값보다 컸는데, 이는 시간 지연이 MR 댐퍼의 제어 효과를 감소시킨다는 것을 의미합니다.
, 이는 시간 지연 없이 최적화된 결과입니다. 제어된 구조 응답의 최대 RMS는 시간 지연과 함께 주기 변동을 나타냈습니다. 변위와 속도의 최대 RMS는 1층에서, 최대 가속도는 6층에서 이루어졌습니다. 또한, 시간 지연이 있는 응답의 모든 최대 MRS는 시간 지연이 없는 값보다 컸는데, 이는 시간 지연이 MR 댐퍼의 제어 효과를 감소시킨다는 것을 의미합니다.

그림 11: TDC-SAC-PSO 방법 제어 구조에 대한 시간 지연과 함께 응답의 최대 RMS. (a) 변위; (b) 속도; (C) 가속도. 약어: RMS = 제곱근 평균 제곱근; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
시간 지연과 함께 변위, 속도 및 가속도의 신뢰성은 그림 12에 나와 있습니다. 속도와 가속도의 신뢰성은 시간 지연과 함께 주기 변동을 보여주는 반면, 변위의 신뢰성은 시간 지연과 함께 급격히 감소했습니다. 모든 시간 지연의 모든 신뢰성 값은 시간 지연이 없는 값보다 작았습니다. 따라서, MR 댐퍼 제어 구조체의 신뢰성에 대한 시간 지연의 영향을 줄이기 위해 시간 지연 보상 방법이 필요하다.
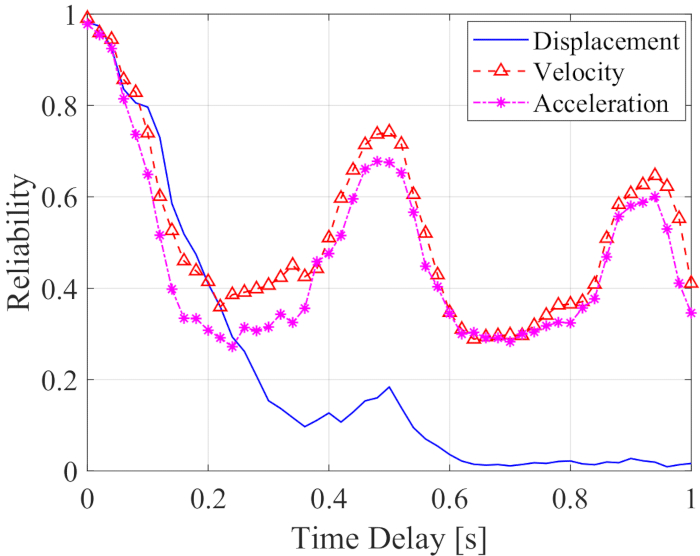
그림 12: 시간 지연과 함께 제어된 구조 응답의 신뢰성. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
3.2 시간 지연 보상의 제어 효과
제안된 TDC-SAC-PSO 방법을 기반으로 두 개의 MR 댐퍼가 있는 6-DOF 구조를 분석했습니다. 그림 13은 제어되지 않음(Unc), TDC-SAC-PSO 방법 제어 및 TDN-SAC-PSO 방법 제어 구조에 대한 1층 및 3층의 변위 및 가속도의 RMS 시간 기록을 보여줍니다. 시간 지연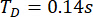 은 이고, 가중치 매트릭스 비율
은 이고, 가중치 매트릭스 비율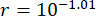 ; MR 댐퍼 매개변수는
; MR 댐퍼 매개변수는  1
1  층에 대한 ,
층에 대한 , 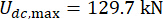 그리고
그리고 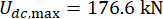 3층에 대한 것이었다.
3층에 대한 것이었다.

그림 13: 서로 다른 방법으로 제어되는 구조물에 대한 1층과 3층의 변위 및 가속도의 RMS 시간 기록. (A) 1층에서의 변위; (B) 3층에서의 변위; (C) 1층에서의 가속 (D) 3층에서 가속. 약어: RMS = 제곱근 평균 제곱근; Unc = 제어되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; TDN -SAC-PSO = 비보상이 제어되는 시간 지연 시스템. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
1층과 3층의 최대 변위 RMS는 시간 지연을 보상하지 않은 TDN-SAC-PSO 방법에 의해 35.42%와 30.44% 감소했습니다. 보상과 함께 1층과 3층의 최대 변위 RMS는 각각 49.33%와 53.39% 감소했습니다. 보상이 없을 경우 1층과 3층의 최대 가속 RMS는 16.22%와 2.88% 증가했으나 각각 25.77%와 36.00% 감소했다. 따라서 MR 댐퍼 제어 방식에서 시간 지연의 보상은 구조물의 응답, 특히 가속도를 줄이기 위해 필요합니다.
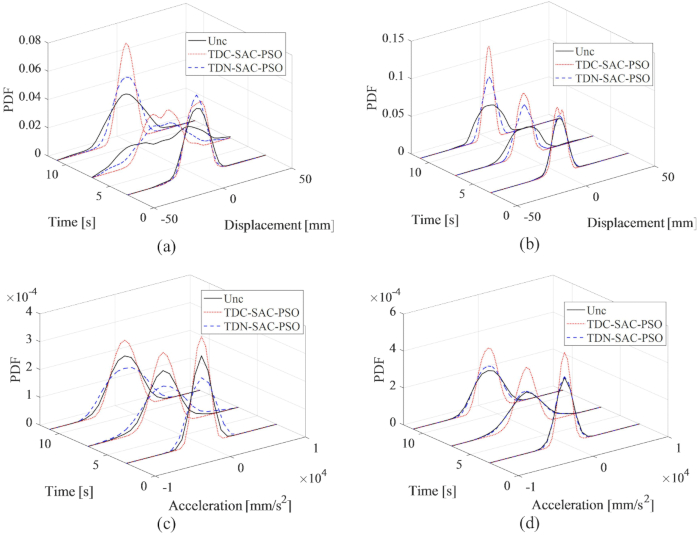
그림 14: 다양한 제어 방법에 대한 1층과 3층의 변위 및 가속도에 대한 PDF. (A) 1층에서의 변위; (B) 3층에서의 변위; (C) 1층에서의 가속 (D) 3층에서 가속. 약어: PDF = 확률 밀도 함수; Unc = 제어되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; TDN -SAC-PSO = 비보상이 제어되는 시간 지연 시스템. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
그림 14에는 1층과 3층의 변위 및 가속도에 대한 PDF가 표시되어 있으며, 이는 제어되지 않은 구조와 비교하여 TDC-SAC-PSO 및 TDN-SAC-PSO 방법의 다른 제어 효과를 보여줍니다. 이에 대한 보상이 없다면, 1층과 3층의 강제이주 PDF는 통제되지 않은 구조물의 PDF보다 여전히 좁았다. 또한 시간 지연을 보상하여 변위의 PDF가 TDN-SAC-PSO 방법 제어 구조의 PDF보다 좁아졌습니다. 보상이 없는 변위와 달리 TDN-SAC-PSO 방식의 1층 가속도 PDF는 제어되지 않은 구조물의 PDF보다 넓었습니다. 그러나 이에 대한 보상으로 1층과 3층의 가속 PDF는 통제되지 않은 구조물의 PDF보다 좁아졌습니다. 따라서, 구조 응답의 확실성, 특히 가속도의 확실성을 증가시키기 위해 시간 지연 보상의 필요성이 검증됩니다.
| 제어 방법 | 변위 | 속도 | 가속도 | 1층 에서 통제력 | 3층 에서 통제력 |
| 유엔 | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
표 4: 다양한 방법으로 제어되는 구조물에 대한 신뢰성. 약어: Unc = 통제되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; TDN -SAC-PSO = 비보상이 제어되는 시간 지연 시스템.
서로 다른 방법으로 제어되는 구조 시스템에 대한 변위, 속도, 가속도 및 제어력의 신뢰성 값은 표 4에 나와 있습니다. 구조 응답의 신뢰도 값은 등가 극한값 방법25를 사용하여 계산되었습니다. TDN-SAC-PSO 방법 제어에 의해 제어되지 않은 구조에 비해 변위의 신뢰성은 증가한 반면 속도 및 가속도의 신뢰성은 감소했습니다. TDC-SAC-PSO 방법의 시간 지연 보상을 통해 변위, 속도 및 가속도의 신뢰성이 크게 향상되었습니다. 또한 TDN-SAC-PSO 및 TDN-SAC-PSO 방법 모두에 대한 제어력의 신뢰성 값이 충분히 유지됩니다. 따라서, 제안된 시간 지연 보상 제어 방법은 MR 댐퍼 제어 구조체에 대해 유리한 제어 효과를 달성한다.
3.3 매개 변수 최적화
최적의 제어 효과를 달성하기 위해 제안된 제어 방법의 매개변수는 신뢰성 기준에 따라 최적화되었습니다. 시간 지연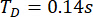 에 의해, 최적 결과는 ;
에 의해, 최적 결과는 ; 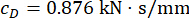 , 1st
, 1st  floor MR damper; 및
floor MR damper; 및 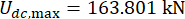 3st floor MR damper
3st floor MR damper 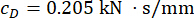 에 대해;
에 대해;
1층과 3층의 변위 및 가속도의 RMS 시간 이력은 TDC-SAC-PSO 및 SOSC-PSO 방법과 제어되지 않은 구조의 제어 효과를 비교하는 그림 15 에 나와 있습니다. MR 댐퍼 제어를 사용하면 시간 지연 보상이 있든 없든 변위 및 가속도의 RMS가 크게 감소했습니다. SOSC-PSO 방법을 사용하면 1층과 3층의 최대 변위 RMS가 제어되지 않은 구조물에 비해 각각 65.15%와 63.16% 감소했습니다. TDC-SAC-PSO 방법과 비교하여 변위 응답이 더욱 감소했습니다. 1층과 3층의 최대 가속도 RMS는 SOSC-PSO 방식의 경우 각각 23.39%, 35.60% 감소합니다. SOSC-PSO 및 TDC-SAC-PSO 방법의 가속 제어 효과에는 거의 차이가 없었으며, 이는 시간 지연 보상의 제어 효과가 변위와 가속도에 대해 다르다는 것을 나타냅니다.
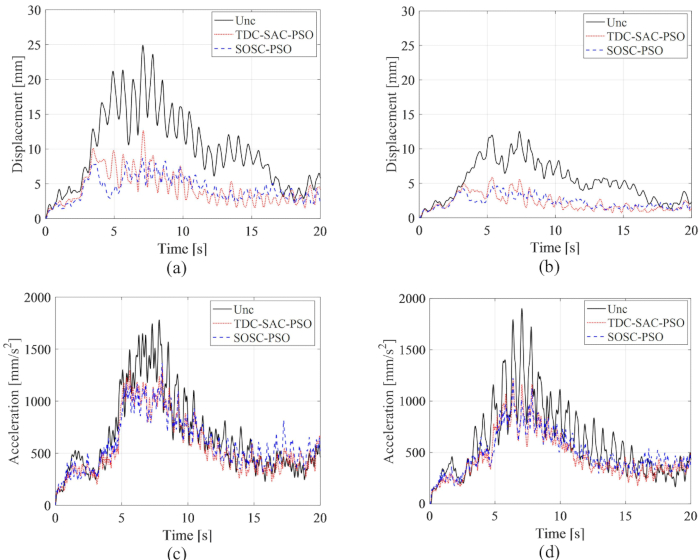
그림 15: 다양한 제어 방법에 대한 1층과 3층의 변위 및 가속도의 RMS 시간 기록. (A) 1층에서의 변위; (B) 3층에서의 변위; (C) 1층에서의 가속 (D) 3층에서 가속. 약어: RMS = 제곱근 평균 제곱근; Unc = 제어되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; SOSC-PSO = 시간 지연 보상을 사용하는 확률적 최적 반능동 제어 방법. 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
1층과 3층의 변위 및 가속도에 대한 PDF는 그림 16에 나와 있습니다. 변위 및 가속도의 PDF는 제어되지 않은 구조와 비교하여 TDC-SAC-PSO 및 SOSC-PSO 방법에 의해 좁혀졌습니다. 또한 SOSC-PSO 방법에 대한 변위 및 가속도의 PDF는 TDC-SAC-PSO 방법 제어 구조의 PDF에 비해 더 좁아졌습니다. 따라서, 파라미터 최적화를 통해, 제안된 시간 지연 보상 제어 방법은 최적화를 하지 않았을 때보다 더 나은 제어 효과를 달성하였다.

그림 16: 다양한 제어 방법에 대한 1층과 3층의 변위 및 가속도에 대한 PDF. (A) 1층에서의 변위; (B) 3층에서의 변위; (C) 1층에서의 가속 (D) 3층에서 가속. 약어: PDF = 확률 밀도 함수; Unc = 제어되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; SOSC-PSO = 시간 지연 보상을 사용한 확률적 최적 반능동 제어 방법 이 그림의 더 큰 버전을 보려면 여기를 클릭하십시오.
변위, 속도, 가속도 및 제어력의 신뢰성 값은 표 5에 나와 있습니다. SOSC-PSO 방법의 신뢰성 값은 TDC-SAC-PSO 방법의 신뢰성 값보다 높았습니다. 한편, 통제군은 여전히 충분한 신뢰성을 유지했습니다. 따라서 MR 댐퍼 기반 제어 방법에 대한 최상의 제어 효과를 달성하기 위해 매개변수의 최적화가 필요합니다.
| 제어 방법 | 변위 | 속도 | 가속도 | 1층 에서 통제력 | 3층 에서 통제력 |
| 유엔 | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
표 5: 다양한 방법으로 제어되는 구조물에 대한 신뢰성. 약어: Unc = 통제되지 않음; TDC-SAC-PSO = 보상이 제어되는 시간 지연 시스템; SOSC-PSO = 시간 지연 보상을 사용하는 확률적 최적 반능동 제어 방법.
결과
본 논문에서는 MR 댐퍼 기반 방식의 제어 효과에 대한 시간 지연의 영향을 목표로 시간 지연 보상을 이용한 반능동 제어 방법을 제안한다. 제안된 방법에서 중요 매개변수는 신뢰성 기준에 따라 최적화됩니다. 통제 효과를 비교하면 다음과 같은 결론을 도출할 수 있습니다.
(1) MR 댐퍼를 기반으로 한 반능동 제어 방식은 능동 제어 방식보다 견고합니다...
토론
본 논문에서는 PSO(Physical Stochastic Optimal Control Theory)를 도입하여 MR 댐퍼에 의해 제어되는 구조물의 신뢰성을 유지하기 위해 설계된 SOSC-PSO(Time Delay Compensation)를 이용한 확률적 최적 반능동 제어 방법을 제안한다. 제안된 방법의 시간 지연을 보상하기 위해 반능동 제어력은 현재 상태뿐만 아니라 이산 상태 공간에서 이전 시간 단계의 상태 및 제어력의 함수로 파생됩니다. ?...
공개
모든 저자는 선언할 이해 상충이 없습니다.
감사의 말
저자는 허베이성 자연과학재단(보조금 번호 E2023210007)의 지원에 감사를 표합니다.
자료
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
참고문헌
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
재인쇄 및 허가
JoVE'article의 텍스트 или 그림을 다시 사용하시려면 허가 살펴보기
허가 살펴보기This article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. 판권 소유