Zum Anzeigen dieser Inhalte ist ein JoVE-Abonnement erforderlich. Melden Sie sich an oder starten Sie Ihre kostenlose Testversion.
Research Article
Stochastische semi-aktive Regelungsmethode der Struktur auf Basis magnetorheologischer Dämpfer unter Berücksichtigung der Zeitverzögerung
In diesem Artikel
Zusammenfassung
In dieser Arbeit wird eine stochastische optimale semiaktive Kontrollmethode mit Zeitverzögerungskompensation (SOSC-PSO) vorgeschlagen, die darauf ausgelegt ist, die Zuverlässigkeit von Strukturen, die durch MR-Dämpfer gesteuert werden, aufrechtzuerhalten.
Zusammenfassung
Der Einsatz von magnetorheologischen (MR) Dämpfern in semiaktiven Regelungssystemen steht vor einer zentralen Herausforderung: Zeitverzögerung durch Rückkopplungsprozesse, die die Zuverlässigkeit von Bauwerken im Bauwesen unter stochastischen Anregungen verringert. In diesem Artikel wird eine stochastische optimale semiaktive Regelungsmethode mit Zeitverzögerungskompensation (SOSC-PSO) vorgeschlagen, die die physikalische stochastische optimale Regelungstheorie (PSO) nutzt, um dieses Problem zu lösen und die strukturelle Zuverlässigkeit zu erhalten. Das vorgeschlagene Verfahren leitet die semiaktive Steuerkraft als Funktion sowohl des aktuellen als auch des vorherigen Zustands ab, wodurch Zeitverzögerungen im Regelungsprozess kompensiert werden. Um die Wirksamkeit der Steuerung zu optimieren, werden wichtige Parameter auf der Grundlage eines Zuverlässigkeitskriteriums für das System abgestimmt. Validierungsanalysen an Strukturen mit einem und mehreren Freiheitsgraden unter stochastischen seismischen Anregungen zeigen, dass Zeitverzögerungen die Leistung von MR-Dämpfern signifikant beeinträchtigen. Die SOSC-PSO-Methode mit Zeitverzögerungskompensation verbessert jedoch die Wirksamkeit der Regelung erheblich und erhöht bei optimierten Parametern die Zuverlässigkeit des strukturellen Kontrollsystems über Methoden ohne Parameteroptimierung hinaus.
Einleitung
Die Verbesserung der Leistung von Ingenieurbauwerken angesichts von Katastrophenereignissen wie Erdbeben und extremen Winden ist nach wie vor ein Hauptanliegen der Bauingenieure. Die strukturelle Kontrolle, eine wirksame Technik zur Reduzierung von Vibrationen, verbessert nachweislich sowohl die Sicherheit als auch die Funktionalität solcher Strukturen 1,2,3. In den letzten Jahrzehnten wurden zu diesem Zweck verschiedene fortschrittliche Methoden und Technologien entwickelt. Diese Verfahren können grob in vier Kategorien eingeteilt werden, basierend auf der Art der Energie, die zum Antrieb der Steuergeräte verwendet wird: aktive, semiaktive, passive und hybride Steuerungssysteme 4,5,6,7.
Bei der aktiven Regelung wird die erforderliche Steuerkraft direkt durch die Steuergeräte aufgebracht, was eine erhebliche Energiemenge 8,9,10 erfordert. Bei der semiaktiven Regelung hingegen werden die Eigenschaften von Steuergeräten (z. B. Dämpfung oder Steifigkeit) auf der Grundlage von Steuersignalen angepasst, wodurch im Vergleich zu aktiven Systemen viel weniger Energie benötigtwird 11. Im Gegensatz dazu beruht die passive Regelung auf der Energiedissipation ohne jegliche externe Energiezufuhr in das System 12,13,14. Hybridsysteme kombinieren die Merkmale von aktiven/semiaktiven und passiven Regelungsstrategien, um eine effektivere Leistungzu erzielen 15. Unter diesen Ansätzen gilt die semiaktive Regelung aufgrund ihres ausgewogenen Verhältnisses zwischen niedrigem Energieverbrauch und hohem Wirkungsgrad als besonders vielversprechend 16,17,18. Der magnetorheologische (MR) Dämpfer gilt mit seinen überlegenen dynamischen Dämpfungseigenschaften als eine der wirksamsten semiaktiven Steuereinrichtungen 19,20,21,22.
Eine Herausforderung ergibt sich jedoch bei semi-aktiven Regelungssystemen, die MR-Dämpfer verwenden, da die Rückkopplungslogik unweigerlich zu Zeitverzögerungen führt. Diese Verzögerungen werden typischerweise durch mehrere Faktoren23, 24, 25 verursacht, einschließlich: (i) die Erfassung und Verarbeitung von Sensordaten, (ii) die Berechnung der erforderlichen Steuerkraft durch die Steuerung26, (iii) die Signalübertragung durch Wandler zu den MR-Dämpfern27 und (iv) die tatsächliche Krafterzeugung durch die MR-Dämpfer selbst28. Solche Zeitverzögerungen können zu Diskrepanzen zwischen der erzeugten Steuerkraft und der von der Struktur erwarteten Kraft führen, wodurch die Wirksamkeit der Steuerung erheblich beeinträchtigtwird 29. Leider berücksichtigen die meisten bestehenden Regelalgorithmen für MR-Dämpfer diese Verzögerungen nicht.
Darüber hinaus muss aufgrund der inhärenten Zufälligkeit katastrophaler Ereignisse jeder effektive semiaktive Steuerungsalgorithmus in der Lage sein, die Leistung unter stochastischen Anregungen aufrechtzuerhalten. Die Regelungsmethode der linearen quadratischen Gauß (LQG), eine klassische stochastische Optimierungstechnik, wurde zur Minderung von Schwingungen in Strukturen untersucht, die mit MR-Dämpfern ausgestattet sind. Zum Beispiel schlugen Dyke et al. eine LQG-Clipped-Optimic-Kontrollstrategie vor, um die seismische Reaktion von Strukturen, die mit MR-Dämpfern ausgestattet sind, unter Verwendung von Beschleunigungsrückkopplung30 zu verbessern. Ying et al. stellten eine nicht-geclippte, semi-aktive stochastische optimale Kontrollstrategie für nichtlineare Strukturen mit MR-Dämpfern vor, die stochastische Mittelwertbildung und dynamische Programmiertechniken einbezog31. Andere Studien haben die modalbasierte LQG-Regelung angewendet, um die seismische Leistung von baseisolierten Gebäuden19 zu verbessern, und ihre Wirksamkeit zur Schwingungsminderung in Windkrafttürmenanalysiert 32. Klassische LQG-Methoden, die weißes Gaußsches Rauschen annehmen, eignen sich jedoch nicht gut, um die nicht-stationäre, nicht-Gaußsche Natur realer Anregungen wie Erdbeben oder starke Winde zu modellieren. Um dies zu adressieren, wurde das Konzept der physikalisch basierten stochastischen optimalen (PSO) Kontrolle entwickelt33,34, das die Einschränkungen traditioneller LQG-Methoden überwindet und einen genaueren Rahmen für den Umgang mit verschiedenen stochastischen Anregungen bietet35. Studien haben gezeigt, dass die PSO-basierte semiaktive stochastische optimale Regelung die Schwingungsminderung sowohl für lineare als auch für nichtlineare Strukturen, die stochastischen seismischen Kräften ausgesetzt sind, signifikant verbessert36.
Daher besteht ein dringender Bedarf an einem robusten semi-aktiven Regelungsverfahren, das Zeitverzögerungen kompensiert und die Zuverlässigkeit von Strukturen, die durch MR-Dämpfer gesteuert werden, erhöht25,37. Um eine optimale Regelungsleistung unter stochastischen Anregungen zu gewährleisten, ist es darüber hinaus unerlässlich, die kritischen Parameter des vorgeschlagenen Regelungsverfahrens unter Verwendung eines zuverlässigkeitsbasierten Ansatzes zu optimieren. Daher wird in dieser Arbeit eine stochastische optimale semiaktive Kontrollmethode mit Zeitverzögerungskompensation (SOSC-PSO) vorgeschlagen, um die Zuverlässigkeit von Strukturen mit MR-Dämpfern zu verbessern.
Protokoll
1. Stochastische optimale semiaktive Regelungsmethode
Da die Regelwirkung eines MR-Dämpfers maßgeblich durch die unvermeidliche Zeitverzögerung beeinflusst wird, wird ein semiaktives Regelungsverfahren mit einem Zeitverzögerungskompensationsalgorithmus entwickelt, um die Leistung der geregelten Struktur zu erhöhen. Außerdem verursacht die Zufälligkeit, die externen Anregungen innewohnt, die offensichtlichen Unsicherheiten dynamischer Reaktionen. Die PSO-Regelung wird eingeführt, um die kritischen Parameter des vorgeschlagenen Verfahrens zur Gewährleistung der Zuverlässigkeit des Struktursteuerungssystems zu optimieren.
1.1 Kompensationsalgorithmus der semiaktiven Regelung
Betrachten Sie ohne Verlust der Allgemeinheit eine n-Freiheitsgrad-Struktur (n-DOF), die durch MR-Dämpfer mit Zeitverzögerung gesteuert wird, deren Bewegungsgleichung bei stochastischen Anregungen gegeben ist durch:
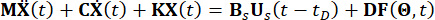 (1)
(1)
Dabei  steht n x n für die Masse-, Dämpfungs- bzw. Steifigkeitsmatrizen der Struktur, n für die Anzahl der Freiheitsgrade der kontrollierten Struktur. Die Verschiebungs-, Geschwindigkeits- und Beschleunigungsvektoren der Struktur werden jeweils durch
steht n x n für die Masse-, Dämpfungs- bzw. Steifigkeitsmatrizen der Struktur, n für die Anzahl der Freiheitsgrade der kontrollierten Struktur. Die Verschiebungs-, Geschwindigkeits- und Beschleunigungsvektoren der Struktur werden jeweils durch 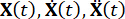 dargestellt. Die kleine Eins und die zwei Punkte über den Symbolen stellen die Ableitungen zum ersten und zweiten Mal dar. Us (t - tD) stellt den r-dimensionalen Vektor der zeitverzögerten Steuerkraft von MR-Dämpfern dar, und r steht für die Anzahl der Dämpfer; t steht für die Zeit; tD bezeichnet die Zeitverzögerung, von der angenommen wird, dass sie über alle Dämpfer in dieser Studie hinweg einheitlich ist, wobei
dargestellt. Die kleine Eins und die zwei Punkte über den Symbolen stellen die Ableitungen zum ersten und zweiten Mal dar. Us (t - tD) stellt den r-dimensionalen Vektor der zeitverzögerten Steuerkraft von MR-Dämpfern dar, und r steht für die Anzahl der Dämpfer; t steht für die Zeit; tD bezeichnet die Zeitverzögerung, von der angenommen wird, dass sie über alle Dämpfer in dieser Studie hinweg einheitlich ist, wobei 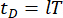 , hier die Integralzahl
, hier die Integralzahl  und
und  die Abtastperiode bezeichnet.
die Abtastperiode bezeichnet. 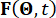 den p-dimensionalen Vektor stochastischer Anregungen darstellt und
den p-dimensionalen Vektor stochastischer Anregungen darstellt und  den stochastischen Parametervektor darstellt, der die Zufälligkeit charakterisiert, die mit externen Anregungen verbunden ist. Die Dimension von
den stochastischen Parametervektor darstellt, der die Zufälligkeit charakterisiert, die mit externen Anregungen verbunden ist. Die Dimension von  hängt von dem Modell ab, das für die externen Anregungen verwendet wird, hängt jedoch nicht mit den mechanischen Freiheitsgraden der Struktur zusammen. Bs und D sind n x r und n x p Matrizen, die die Positionen der Dämpfer bzw. der externen Anregungen angeben. In der Zustandsraumdarstellung wird Gl. (1) wie folgt geschrieben:
hängt von dem Modell ab, das für die externen Anregungen verwendet wird, hängt jedoch nicht mit den mechanischen Freiheitsgraden der Struktur zusammen. Bs und D sind n x r und n x p Matrizen, die die Positionen der Dämpfer bzw. der externen Anregungen angeben. In der Zustandsraumdarstellung wird Gl. (1) wie folgt geschrieben:
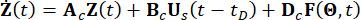 (2)
(2)
Wobei 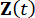 der 2n-dimensionale Zustandsvektor darstellt;
der 2n-dimensionale Zustandsvektor darstellt; 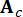 2n x 2n Systemmatrix darstellt;
2n x 2n Systemmatrix darstellt; 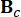 2n x r Positionsmatrix von MR-Dämpfern darstellt;
2n x r Positionsmatrix von MR-Dämpfern darstellt; 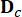 stellt die Ortsmatrix 2n x p der externen Anregungen dar. Diese Parameter werden wie folgt ausgedrückt:
stellt die Ortsmatrix 2n x p der externen Anregungen dar. Diese Parameter werden wie folgt ausgedrückt:
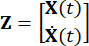 ,
, 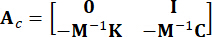 ,
, 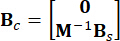 , (
, (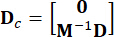 3)
3)
Wobei  eine Identitätsmatrix mit der gleichen Ordnung von
eine Identitätsmatrix mit der gleichen Ordnung von 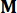 bezeichnet wird. Zur Vereinfachung der Berechnung kann die stetige Zustandsraumgleichung Gl. (2) in diskreter Form ausgedrückt werden als:
bezeichnet wird. Zur Vereinfachung der Berechnung kann die stetige Zustandsraumgleichung Gl. (2) in diskreter Form ausgedrückt werden als:
 (4)
(4)
Wobei der Zeitpunkt  vereinfacht ist als
vereinfacht ist als 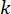 . Und ,
. Und , 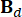 ,
, 
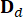 bezeichnen 2n x 2n, 2n x r und 2n x p Matrizen, die ausgedrückt werden als:
bezeichnen 2n x 2n, 2n x r und 2n x p Matrizen, die ausgedrückt werden als:
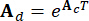 ,
, 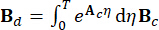 ,
, 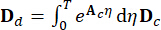 (5)
(5)
Dabei 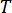 steht für den Probenahmezeitraum.
steht für den Probenahmezeitraum.
Um eine ähnliche Wirksamkeit wie bei der aktiven Regelung zu erreichen, wird für die MR-Dämpfer-basierte Regelung mit Zeitverzögerung ein einfaches und effizientes Regelungsverfahren auf Basis des Hrovat Algorithmus38 vorgeschlagen:
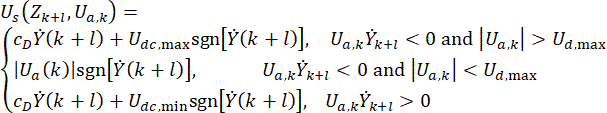 (6)
(6)
wobei 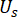 das semiaktive Steuerkraftsignal zum Zeitpunkt
das semiaktive Steuerkraftsignal zum Zeitpunkt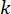 des MR-Dämpfers darstellt;
des MR-Dämpfers darstellt; 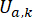 stellt die aktive Referenzsteuerkraft mit Zeitverzögerungskompensation dar;
stellt die aktive Referenzsteuerkraft mit Zeitverzögerungskompensation dar;  stellt die maximale Dämpfkraft des MR-Dämpfers dar, die veränderbar ist;
stellt die maximale Dämpfkraft des MR-Dämpfers dar, die veränderbar ist; 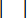 stellt das Symbol für die Absolutwertoperation dar;
stellt das Symbol für die Absolutwertoperation dar; 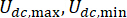 stellen die maximalen und minimalen Coulomb-Kräfte des MR-Dämpfers dar;
stellen die maximalen und minimalen Coulomb-Kräfte des MR-Dämpfers dar; 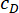 stellt den viskosen Dämpfungskoeffizienten dar;
stellt den viskosen Dämpfungskoeffizienten dar; 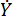 stellt die in den MR-Dämpfer eingegebene Geschwindigkeit dar, d. h. die Bewegungsgeschwindigkeit des Kolbens relativ zum Dämpferzylinder. In Gl. (6)
stellt die in den MR-Dämpfer eingegebene Geschwindigkeit dar, d. h. die Bewegungsgeschwindigkeit des Kolbens relativ zum Dämpferzylinder. In Gl. (6) 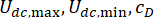 sind die ausgelegten Parameter des MR-Dämpfers dargestellt.
sind die ausgelegten Parameter des MR-Dämpfers dargestellt.
Gl. (6) zeigt die Berechnung der semiaktiven Steuerkraft des MR-Dämpfers mit Zeitverzögerung. Es ist ersichtlich, dass die semiaktive Steuerkraft 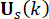 im Zeitschritt
im Zeitschritt 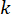 in Gl. (4) auf der Grundlage der aktiven Steuerkraft
in Gl. (4) auf der Grundlage der aktiven Steuerkraft  im Zeitschritt
im Zeitschritt 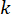 und der Zustandsvariablen
und der Zustandsvariablen 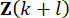 im Zeitschritt
im Zeitschritt 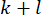 seit der Verzögerung der
seit der Verzögerung der 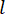 Zeitschritte berechnet wird. Um die aktive Regelkraft
Zeitschritte berechnet wird. Um die aktive Regelkraft  zu erhalten, wird die konventionelle Kostenfunktion durch
zu erhalten, wird die konventionelle Kostenfunktion durch
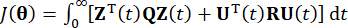 (7)
(7)
Dabei  steht für die symmetrische positive semi-definite Gewichtungsmatrix von 2n x 2n des Systemzustands;
steht für die symmetrische positive semi-definite Gewichtungsmatrix von 2n x 2n des Systemzustands; 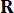 stellt die symmetrische positive definite Gewichtungsmatrix r x r der Steuerkraft dar. Es zeigt sich, dass die äußere Erregung vernachlässigbar ist. Tatsächlich kann das Strukturkontrollsystem auf der Grundlage von Gl. (7) unabhängig von der Art der externen Anregung den optimalen Steuerungseffekt erzielen. Als diskrete Form wird Gl. (7) wie folgt ausgedrückt:
stellt die symmetrische positive definite Gewichtungsmatrix r x r der Steuerkraft dar. Es zeigt sich, dass die äußere Erregung vernachlässigbar ist. Tatsächlich kann das Strukturkontrollsystem auf der Grundlage von Gl. (7) unabhängig von der Art der externen Anregung den optimalen Steuerungseffekt erzielen. Als diskrete Form wird Gl. (7) wie folgt ausgedrückt:
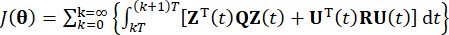 (8)
(8)
Die Minimierung der Kostenfunktion  führt zu einem bedingten Extremwertproblem, und die aktive Kontrollkraft
führt zu einem bedingten Extremwertproblem, und die aktive Kontrollkraft 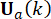 wird durch25 berechnet:
wird durch25 berechnet:
 (9)
(9)
Dabei 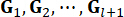 bezeichnen die Kontrollgewinne für die Zustandsvariable
bezeichnen die Kontrollgewinne für die Zustandsvariable 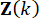 im Zeitschritt
im Zeitschritt 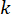 und die aktive Steuerkraft
und die aktive Steuerkraft 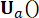 im Zeitschritt
im Zeitschritt  ,
, 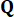 die durch die Gewichtungsmatrizen bestimmt werden, und
die durch die Gewichtungsmatrizen bestimmt werden, und 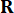 37. Seit der unvermeidlichen Zeitverzögerung werden die erhaltenen Steuerkräfte
37. Seit der unvermeidlichen Zeitverzögerung werden die erhaltenen Steuerkräfte  zu Zeitpunkten
zu Zeitpunkten 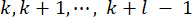 auf die Struktur einwirken. Daher wird die aktive Steuerkraft in Gl. (9) berechnet durch:
auf die Struktur einwirken. Daher wird die aktive Steuerkraft in Gl. (9) berechnet durch:
 (10)
(10)
Zur Verdeutlichung der Konzeption wird die semiaktive Kontrollkraft in Gl. (10) in Anlehnung an Gl. (6) wie folgt ausgedrückt:
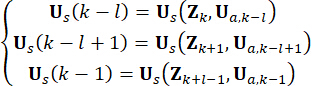 (11)
(11)
Dabei 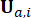 steht für die aktive Steuerkraft zum Zeitpunkt
steht für die aktive Steuerkraft zum Zeitpunkt  . Ersetzen von Gl. (11) durch Gl. (10),
. Ersetzen von Gl. (11) durch Gl. (10),
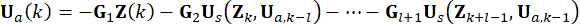 (12)
(12)
HINWEIS: Alle Zustandswerte  vom Zeitpunkt
vom Zeitpunkt 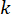 bis
bis 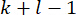 werden für die Berechnung
werden für die Berechnung  von benötigt. Daher wird das folgende Zustandsvorhersageverfahren40 eingeführt.
von benötigt. Daher wird das folgende Zustandsvorhersageverfahren40 eingeführt.
 (13)
(13)
Dabei  wird die vorhergesagte Variable angegeben. Durch die Iteration von Gl. (13) wird der Zustand
wird die vorhergesagte Variable angegeben. Durch die Iteration von Gl. (13) wird der Zustand  at
at 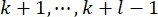 berechnet. Die aktive Steuerkraft Ua(k) wird ausgedrückt als:
berechnet. Die aktive Steuerkraft Ua(k) wird ausgedrückt als:
 (14)
(14)
Die semiaktive Steuerkraft kann durch die Kombination von Gl. (6), (12) und (13).
1.2 Zuverlässigkeitsanalyse des Strukturleitsystems
Nach dem Prinzip der Wahrscheinlichkeitserhaltung sind das augmentierte System 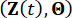 und
und  die Struktur mit MR-Dämpfern wahrscheinlichkeitskonserviert und unterliegen den folgenden verallgemeinerten Wahrscheinlichkeitsdichte-Entwicklungsgleichungen (GDEEs)38:
die Struktur mit MR-Dämpfern wahrscheinlichkeitskonserviert und unterliegen den folgenden verallgemeinerten Wahrscheinlichkeitsdichte-Entwicklungsgleichungen (GDEEs)38:
 (15)
(15)
 (16)
(16)
Dabei bezeichnen die entsprechenden Komponenten des Systemzustands bzw. der semiaktiven Steuerkraft mit Zeitverzögerung und 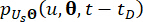
 bezeichnen die gemeinsamen Wahrscheinlichkeitsdichtefunktionen von erweiterten Stichprobensystemen
bezeichnen die gemeinsamen Wahrscheinlichkeitsdichtefunktionen von erweiterten Stichprobensystemen 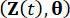 bzw
bzw
 . , bezeichnen die Stichprobe innerhalb des Probenraums von
. , bezeichnen die Stichprobe innerhalb des Probenraums von  und
und 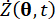 )
) 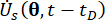 bezeichnen die partiellen Ableitungen der Zeit erster Ordnung des Systemzustands bzw. semiaktive Steuerkraftkomponenten.
bezeichnen die partiellen Ableitungen der Zeit erster Ordnung des Systemzustands bzw. semiaktive Steuerkraftkomponenten.
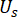 Die Funktion
Die Funktion  der gemeinsamen Wahrscheinlichkeitsdichte kann
der gemeinsamen Wahrscheinlichkeitsdichte kann 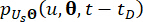 durch Lösen von Gl. erreicht werden. 15 und 16 unter folgenden Ausgangsbedingungen:
durch Lösen von Gl. erreicht werden. 15 und 16 unter folgenden Ausgangsbedingungen:
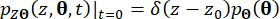 (17)
(17)
 (18)
(18)
Dabei  steht für die Dirac-Delta-Funktion;
steht für die Dirac-Delta-Funktion; 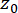 und
und 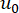 bezeichnen die deterministischen Anfangswerte von
bezeichnen die deterministischen Anfangswerte von 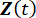 bzw
bzw 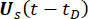 . , bezeichnet
. , bezeichnet  die Wahrscheinlichkeitsdichtefunktion der Stichprobe
die Wahrscheinlichkeitsdichtefunktion der Stichprobe 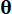 .
.
Die momentanen Wahrscheinlichkeitsdichtefunktionen von 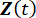 und
und 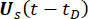 können durch die eindimensionale Integration von
können durch die eindimensionale Integration von  und
und 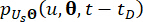 über den Bereich des Probenraums erhalten werden:
über den Bereich des Probenraums erhalten werden:
 (19)
(19)
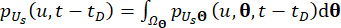 (20)
(20)
Dabei 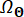 wird die Verteilungsdomäne von
wird die Verteilungsdomäne von  bezeichnet.
bezeichnet.
Basierend auf Gl. (19) und (20) zeigt sich, dass die vollständigen probabilistischen Informationen der betreffenden physikalischen Größen leicht abgeleitet werden können, wenn ihre Beziehungen zu den Parametern des Algorithmus definiert werden. Die Zuverlässigkeit der betreffenden physikalischen Größen kann durch die folgende relevante Leistungsfunktion berechnet werden:
 (21)
(21)
 (22)
(22)
wobei 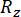 und
und 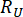 die berechnete Zuverlässigkeit der betreffenden Zustandsgröße bzw
die berechnete Zuverlässigkeit der betreffenden Zustandsgröße bzw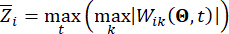 . der semiaktiven Steuerkraft bezeichnet; den äquivalenten Extremwertvektor der i-ten betroffenen physikalischen Größe der kontrollierten Struktur bezeichnet;
. der semiaktiven Steuerkraft bezeichnet; den äquivalenten Extremwertvektor der i-ten betroffenen physikalischen Größe der kontrollierten Struktur bezeichnet; 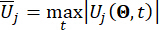 den äquivalenten Extremwertvektor der j-ten Steuerkraft bezeichnet; der Hut '-' auf Symbolen den äquivalenten Extremwertvektor41 angibt;
den äquivalenten Extremwertvektor der j-ten Steuerkraft bezeichnet; der Hut '-' auf Symbolen den äquivalenten Extremwertvektor41 angibt; 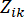 bezeichnet die i-te betroffene physikalische Größe der k-ten Schärfentiefe der kontrollierten Struktur;
bezeichnet die i-te betroffene physikalische Größe der k-ten Schärfentiefe der kontrollierten Struktur; 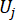 bezeichnet die j-te Kontrollkraft;
bezeichnet die j-te Kontrollkraft;  ,
, 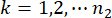 ,
, 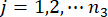 , und
, und 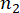
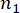
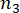 bezeichnen die Anzahl der betroffenen physikalischen Größen und den Freiheitsgrad der Struktur bzw. der MR-Dämpfer, die in die Struktur eingebaut sind,
bezeichnen die Anzahl der betroffenen physikalischen Größen und den Freiheitsgrad der Struktur bzw. der MR-Dämpfer, die in die Struktur eingebaut sind, 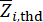 und
und  bezeichnen die Schwellenwerte von
bezeichnen die Schwellenwerte von 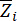 und
und  ;
;  bezeichnet die Wahrscheinlichkeit des Zufallsereignisses.
bezeichnet die Wahrscheinlichkeit des Zufallsereignisses.
1.3 Optimierung der Parameter
Das Verhältnis der Amplituden von und 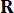 beeinflusst die Wirksamkeit der
beeinflusst die Wirksamkeit der  Steuerung38 in der Regelungsmodalität der Rückkopplung in hohem Maße. Um die beste Wirksamkeit der Kontrolle zu erreichen,
Steuerung38 in der Regelungsmodalität der Rückkopplung in hohem Maße. Um die beste Wirksamkeit der Kontrolle zu erreichen,
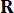 müssen diese daher optimiert werden. Da es sich um eine MR-Dämpfer-basierte Regelungsmethode handelt, wird die Wirksamkeit der Regelung auch von den Geräteparametern beeinflusst,
müssen diese daher optimiert werden. Da es sich um eine MR-Dämpfer-basierte Regelungsmethode handelt, wird die Wirksamkeit der Regelung auch von den Geräteparametern beeinflusst, 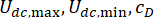 siehe Gl. (6). Um die optimale Zuverlässigkeit des Struktursteuerungssystems zu erreichen, wird in Gl. (25) das auf Zuverlässigkeit basierende Kriterium vorgeschlagen.
siehe Gl. (6). Um die optimale Zuverlässigkeit des Struktursteuerungssystems zu erreichen, wird in Gl. (25) das auf Zuverlässigkeit basierende Kriterium vorgeschlagen.

Abbildung 1: Flussdiagramm der Parameteroptimierung für eine stochastisch optimale semiaktive Strukturregelung mit Zeitverzögerungskompensation. Abkürzungen: GDEE = Verallgemeinerte Differentialgleichung des Ereignisses ; PDF = Wahrscheinlichkeitsdichte-Funktion. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Zusammenfassend sind zwei Stufen erforderlich, um die stochastisch optimale semiaktive Strukturregelung auf Basis von MR-Dämpfern mit Zeitverzögerungskompensation durchzuführen:
1.3.1 Durch Minimierung der in Gl. (7) gezeigten Kostenfunktion  wird die Zustandsrückkopplungslogik im Sinne von Stichproben erreicht, d.h. Gl. 12)
wird die Zustandsrückkopplungslogik im Sinne von Stichproben erreicht, d.h. Gl. 12)
1.3.2 Durch die Minimierung der zuverlässigkeitsbasierten Leistungsfunktion  werden die optimalen Parameter im Sinne der Statistik erreicht. Abbildung 1 zeigt das Optimierungsflussdiagramm der Parameter des Reglers in Schritt 1.3.2.
werden die optimalen Parameter im Sinne der Statistik erreicht. Abbildung 1 zeigt das Optimierungsflussdiagramm der Parameter des Reglers in Schritt 1.3.2.
Die folgenden Schritte in Schritt 1.3.2, die zwei Schichten von Schleifen umfassen, lauten wie folgt:
1.3.2.1 Die Partitionierung des Wahrscheinlichkeitsraums stochastischer Anregungen, der durch den stochastischen Parametervektor 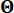 charakterisiert ist, ermöglicht die Identifizierung einer Menge repräsentativer Punkte
charakterisiert ist, ermöglicht die Identifizierung einer Menge repräsentativer Punkte  zusammen mit den ihnen zugeordneten WahrscheinlichkeitenPq. Dieser Ansatz ermöglicht die effiziente Erzeugung von Probenprozessen für die stochastische Anregung, die als
zusammen mit den ihnen zugeordneten WahrscheinlichkeitenPq. Dieser Ansatz ermöglicht die effiziente Erzeugung von Probenprozessen für die stochastische Anregung, die als 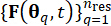 bezeichnet wird, ohne weiteres zu erhalten.
bezeichnet wird, ohne weiteres zu erhalten.
1.3.2.2 Für die Parameteroptimierung des semiaktiven Struktursteuerungssystems initialisieren oder aktualisieren Sie die Werte der Kosten-Funktionsgewichte  und
und 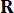 . Die zugehörige Zustandsrückkopplungs-Steuerkraft mit Zeitverzögerung, siehe Gl. (12), wird dann berechnet.
. Die zugehörige Zustandsrückkopplungs-Steuerkraft mit Zeitverzögerung, siehe Gl. (12), wird dann berechnet.
1.3.2.3 Ermittlung der Wahrscheinlichkeitsdichtefunktionen (PDFs) der strukturellen Reaktionen und der Kontrollkraft durch Lösen der in Gl. gezeigten GDEEs. (17)–(20):
Die Optimierung erfolgt offline, aber nicht online. Bei der Anwendung des vorgeschlagenen Verfahrens in realen Strukturkontrollsystemen wurden die optimalen  und
und 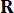 erreicht, und die Optimierung ist im real anwendbaren Prozess nicht erforderlich.
erreicht, und die Optimierung ist im real anwendbaren Prozess nicht erforderlich.
Deterministische dynamische Analyse des semiaktiven Strukturkontrollsystems unter Probenanregung, mit der die betreffenden physikalischen Größen 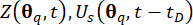 und ihre Ableitungen
und ihre Ableitungen  berechnet werden.
berechnet werden.
Durch die Verwendung einer Finite-Differenzen-Methode, wie z.B. dem modifizierten Lax-Wendroff-Schema mit Total Variation Diminishing(TVD)-Eigenschaften, können die verallgemeinerten Differentialgleichungen (GDEEs) gelöst und numerische Lösungen für die gemeinsamen Wahrscheinlichkeitsdichtefunktionen 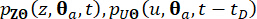 abgeleitet werden.
abgeleitet werden.
Wenn man die beiden obigen Schritte der deterministischen dynamischen Analyse und der Finite-Differenzen-Methode wiederholt und über alle repräsentativen Punkte 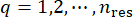 läuft, können die Wahrscheinlichkeitsdichtefunktionen durch Summierung erhalten werden:
läuft, können die Wahrscheinlichkeitsdichtefunktionen durch Summierung erhalten werden:
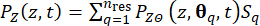 (23)
(23)
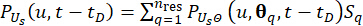 (24)
(24)
Dabei 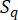 steht für das Flächenmaß des Subbereichs, der dem Abtastpunkt
steht für das Flächenmaß des Subbereichs, der dem Abtastpunkt  zugeordnet ist. Die Methode, die zur Lösung der verallgemeinerten Differentialgleichung des Ereignisses (GDEE) verwendet wird, ist als Wahrscheinlichkeitsdichte-Evolutionsmethode (PDEM)42 bekannt.
zugeordnet ist. Die Methode, die zur Lösung der verallgemeinerten Differentialgleichung des Ereignisses (GDEE) verwendet wird, ist als Wahrscheinlichkeitsdichte-Evolutionsmethode (PDEM)42 bekannt.
1.3.2.4 Zur Bewertung ihrer Zuverlässigkeit werden die PDFs der relevanten physikalischen Größen verwendet, die dann in die Leistungsfunktion  des probabilistischen Kriteriums einfließen.
des probabilistischen Kriteriums einfließen.
1.3.2.5 Bewerten Sie, ob die Abbruchkriterien für den Parameteroptimierungsprozess erfüllt wurden. Sind die Bedingungen nicht erfüllt, kehren Sie zu Schritt 1.3.2.2 zurück. Ist dies der Fall, können die optimalen Parameter für die zeitversetzte Steuerung ermittelt werden. In dieser Arbeit wird die Toolbox des genetischen Algorithmus (GA) in MATLAB zur Parameteroptimierung verwendet, die Parameteraktualisierungen erleichtert und die Beendigungsbedingungen definiert. Durch einen genetischen Algorithmus können die optimalen Werte innerhalb von zehn Iterationen erreicht werden, und die Konvergenz ist stabil ohne lokale Minima-Probleme. Obwohl der Rechenaufwand der GA größer ist als bei der Partikelschwarmoptimierung oder gradientenbasierten Methoden, ist die GA gut darin, mit komplexen und nicht differenzierbaren Problemen, wie dem in diesem Manuskript, umzugehen. Daher wird die GA angewendet. Und da es sich um eine schnelle Konvergenzeigenschaft handelt, ist der Rechenaufwand von GA akzeptabel.
1.3.2.6 Um eine optimale Zuverlässigkeitsregelung zu erreichen, wird die folgende Leistungsfunktion  formuliert. Minimieren
formuliert. Minimieren  , um die optimalen Werte von Parametern
, um die optimalen Werte von Parametern 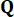 zu ermitteln und
zu ermitteln und  :
:
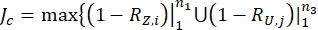 } (25)
} (25)
 (26)
(26)
Wie bereits erwähnt, sind die Gewichtungsmatrizen des Reglers symmetrisch, wobei die Elemente in der Matrix 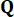 den Gewichten entsprechen, die der Verschiebung, der Geschwindigkeit und ihrer Wechselwirkung zugewiesen sind, während die Elemente in der Matrix
den Gewichten entsprechen, die der Verschiebung, der Geschwindigkeit und ihrer Wechselwirkung zugewiesen sind, während die Elemente in der Matrix  die Gewichte darstellen, die sich auf die Steuerkraft beziehen. Basierend auf den Ergebnissen früherer Studien38 wurde beobachtet, dass die Variation der Konfigurationen der Kosten-Funktionsgewichte
die Gewichte darstellen, die sich auf die Steuerkraft beziehen. Basierend auf den Ergebnissen früherer Studien38 wurde beobachtet, dass die Variation der Konfigurationen der Kosten-Funktionsgewichte 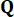
 nur minimale Auswirkungen auf die Wirksamkeit der Kontrolle hat. Daher wird in dieser Studie eine vereinfachte Konfiguration gewählt, die im Folgenden beschrieben wird:
nur minimale Auswirkungen auf die Wirksamkeit der Kontrolle hat. Daher wird in dieser Studie eine vereinfachte Konfiguration gewählt, die im Folgenden beschrieben wird:
 ,
,  (27)
(27)
Dabei 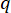 bezeichnet den Koeffizienten der zu definierenden Zustandsgewichtungsmatrix;
bezeichnet den Koeffizienten der zu definierenden Zustandsgewichtungsmatrix; 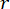 bezeichnet den Koeffizienten der zu definierenden Kontrollgewichtungsmatrix;
bezeichnet den Koeffizienten der zu definierenden Kontrollgewichtungsmatrix;  bezeichnet die Identitätsmatrix. Der Kontrolleffekt wird durch das Verhältnis von
bezeichnet die Identitätsmatrix. Der Kontrolleffekt wird durch das Verhältnis von 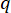 zu beeinflusst,
zu beeinflusst, 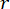 nicht aber durch die Werte selbst.
nicht aber durch die Werte selbst. 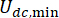 Außerdem bezeichnet in Gl. (6) die minimale Coulombkraft des MR-Dämpfers, was bedeutet, dass
Außerdem bezeichnet in Gl. (6) die minimale Coulombkraft des MR-Dämpfers, was bedeutet, dass 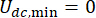 der Stromeingang im Dämpfer Null ist. Dann kann Gl. (26) weiter ausgedrückt werden als:T
der Stromeingang im Dämpfer Null ist. Dann kann Gl. (26) weiter ausgedrückt werden als:T
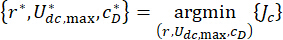 (28)
(28)
Wo 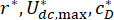 sind die optimalen Betreffskoeffizienten? Um sie im Engineering sinnvoll zu gestalten, basieren die optimalen Reichweiten auf der Produktionskapazität der MR-Dämpferwerke.
sind die optimalen Betreffskoeffizienten? Um sie im Engineering sinnvoll zu gestalten, basieren die optimalen Reichweiten auf der Produktionskapazität der MR-Dämpferwerke.
Offensichtlich behalten die optimalen Parameter, die durch Gl. (28) erhalten werden, die optimale Regelungswirksamkeit des vorgeschlagenen semi-aktiven Regelungsalgorithmus mit Zeitverzögerung bei, was es dem Struktursteuerungssystem ermöglicht, die ausgewogene optimale Zuverlässigkeit bei stochastischen Anregungen zu erreichen.
2. Fallstudie
Um die Wirksamkeit der vorgeschlagenen semi-aktiven Regelungsmethode mit Zeitverzögerungskompensation für einen MR-Dämpfer zu analysieren, wurde eine planare einstöckige Schubrahmenstruktur, die an einem MR-Dämpfer befestigt war, der horizontalen stochastischen seismischen Bodenbewegung ausgesetzt, wie in Abbildung 2 gezeigt. Die Parameter des semi-aktiv gesteuerten Struktursystems sind wie folgt: Strukturmasse 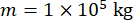 , natürliche Kreisfrequenz
, natürliche Kreisfrequenz 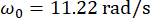 , Dämpfungsverhältnis
, Dämpfungsverhältnis 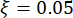 . Nach bisherigen Erfahrungen und bestehenden Dämpferwaagen auf dem Markt liegen die Schwellenwerte für strukturelle Verschiebung, Geschwindigkeit, Beschleunigung und Steuerkraft bei 10 mm, 100 mm/s, 1.500 mm/s2 bzw. 150 kN. Zur Darstellung der stochastischen seismischen Bodenbewegung wurde das physikalisch motivierte stochastische Bodenbewegungsmodell verwendet43:
. Nach bisherigen Erfahrungen und bestehenden Dämpferwaagen auf dem Markt liegen die Schwellenwerte für strukturelle Verschiebung, Geschwindigkeit, Beschleunigung und Steuerkraft bei 10 mm, 100 mm/s, 1.500 mm/s2 bzw. 150 kN. Zur Darstellung der stochastischen seismischen Bodenbewegung wurde das physikalisch motivierte stochastische Bodenbewegungsmodell verwendet43:
 (29)
(29)
Dabei 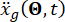 steht für die Bodenbewegung im Zeitbereich am Ingenieurstandort und
steht für die Bodenbewegung im Zeitbereich am Ingenieurstandort und 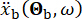 bezeichnet die Bodenbewegung im Frequenzbereich am Grundgestein. Der Vektor
bezeichnet die Bodenbewegung im Frequenzbereich am Grundgestein. Der Vektor 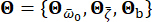 charakterisiert die stochastische Natur der Bodenbewegung an der Oberfläche des Ingenieurstandorts. Bei den Parametern
charakterisiert die stochastische Natur der Bodenbewegung an der Oberfläche des Ingenieurstandorts. Bei den Parametern 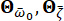 handelt es sich um stochastische Variablen, die die Eigenschaften des Standortbodens beschreiben, einschließlich der vorherrschenden Häufigkeit
handelt es sich um stochastische Variablen, die die Eigenschaften des Standortbodens beschreiben, einschließlich der vorherrschenden Häufigkeit 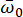 und der äquivalenten Dämpfung
und der äquivalenten Dämpfung 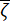 . Der Vektor
. Der Vektor 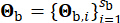 stellt die stochastische Natur der Bodenbewegung am Grundgestein dar, die von den Eigenschaften der Quelle und dem Ausbreitungsweg beeinflusst wird, wobei
stellt die stochastische Natur der Bodenbewegung am Grundgestein dar, die von den Eigenschaften der Quelle und dem Ausbreitungsweg beeinflusst wird, wobei 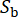 er die Anzahl der stochastischen Variablen angibt, die in dieser Phase beteiligt sind.
er die Anzahl der stochastischen Variablen angibt, die in dieser Phase beteiligt sind. 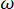 bezieht sich auf die Kreisfrequenz, und i ist die imaginäre Einheit.
bezieht sich auf die Kreisfrequenz, und i ist die imaginäre Einheit.
Die vorherrschende Frequenz  und das äquivalente Dämpfungsverhältnis des Baustellengeländes
und das äquivalente Dämpfungsverhältnis des Baustellengeländes 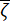 sind Schlüsselparameter, die die dynamischen Eigenschaften des Baustellenbodens charakterisieren. Die probabilistische Verteilung und die statistischen Parameter dieser Größen können auf der Grundlage von seismischen Beschleunigungsaufzeichnungen bestimmt werden, die von einer bestimmten Klasse von Ingenieurstandorten gesammelt wurden. Zur Veranschaulichung wurde eine Standortklasse mit einem Scherwellengeschwindigkeitsbereich von [150, 250] m/s betrachtet und die für die Konstruktion charakteristische Periode der Bodenbewegung auf 0,45 s festgelegt.
sind Schlüsselparameter, die die dynamischen Eigenschaften des Baustellenbodens charakterisieren. Die probabilistische Verteilung und die statistischen Parameter dieser Größen können auf der Grundlage von seismischen Beschleunigungsaufzeichnungen bestimmt werden, die von einer bestimmten Klasse von Ingenieurstandorten gesammelt wurden. Zur Veranschaulichung wurde eine Standortklasse mit einem Scherwellengeschwindigkeitsbereich von [150, 250] m/s betrachtet und die für die Konstruktion charakteristische Periode der Bodenbewegung auf 0,45 s festgelegt.
Die kritischen Parameter 
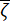 wurden als voneinander unabhängige stochastische Variablen behandelt, die beide einer logarithmischen Normalverteilung zur Parameteridentifikation folgten. Die statistischen Parameter waren wie folgt: Die Mittelwerte von
wurden als voneinander unabhängige stochastische Variablen behandelt, die beide einer logarithmischen Normalverteilung zur Parameteridentifikation folgten. Die statistischen Parameter waren wie folgt: Die Mittelwerte von  betrugen
betrugen 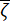 12 rad/s bzw. 0,1. Die Variationskoeffizienten von
12 rad/s bzw. 0,1. Die Variationskoeffizienten von  und
und 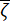 betrugen 0,42 bzw. 0,35. Die Bodenbewegung am Grundgestein wurde als Gaußscher Prozess des weißen Rauschens mit einer Fourier-Amplitude von 0,20 m/s2 modelliert, was einer maximalen Bodenbeschleunigung von 0,11 g entspricht. Der Phasenwinkel, der zur Erzeugung der Grundgesteinsbewegung verwendet wurde, wurde als
betrugen 0,42 bzw. 0,35. Die Bodenbewegung am Grundgestein wurde als Gaußscher Prozess des weißen Rauschens mit einer Fourier-Amplitude von 0,20 m/s2 modelliert, was einer maximalen Bodenbeschleunigung von 0,11 g entspricht. Der Phasenwinkel, der zur Erzeugung der Grundgesteinsbewegung verwendet wurde, wurde als 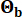 bezeichnet. Daher ist Sb = 1 und
bezeichnet. Daher ist Sb = 1 und 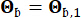 . Dieser Ansatz kann als Modellierung bedingter stochastischer Bodenbewegungen mit einer gegebenen Überschreitungswahrscheinlichkeit44 betrachtet werden. Die Annahme der logarithmischen Normalverteilung wird in der Modellierung von Bodenbewegungen häufig verwendet, da sie die verzerrte Natur der beobachteten Bodenbewegungsparameter erfassen kann.
. Dieser Ansatz kann als Modellierung bedingter stochastischer Bodenbewegungen mit einer gegebenen Überschreitungswahrscheinlichkeit44 betrachtet werden. Die Annahme der logarithmischen Normalverteilung wird in der Modellierung von Bodenbewegungen häufig verwendet, da sie die verzerrte Natur der beobachteten Bodenbewegungsparameter erfassen kann.
Um die Sensitivität dieser Annahme zu beurteilen, wurden die zusätzlichen Analysen mit alternativen probabilistischen Verteilungen, einschließlich der Normal- und Gammaverteilung, in anderen Untersuchungen durchgeführt45,46. Die Ergebnisse deuten darauf hin, dass die Gesamttrends zwar konsistent bleiben, die logarithmisch-normale Verteilung jedoch die beste Anpassung an die beobachteten Daten bietet, insbesondere für die Erfassung des Schweifverhaltens von Messungen der Bodenbewegungsintensität
Mittels der Tangentensphärenmethode47 wurde eine Sammlung von 221 repräsentativen Punkten mit zugehörigen zugeordneten Wahrscheinlichkeiten ausgewählt und repräsentative Bodenbeschleunigungen synthetisiert. Die Abtastfrequenz betrug 50 Hz, und die Dauer der Bodenbewegungen betrug 20,48 s. Um der simulierten Bodenbewegung eine nichtstationäre Intensität zuzuweisen, wurde eine einheitliche Modulationsfunktion verwendet, die wie folgt formuliert war42:
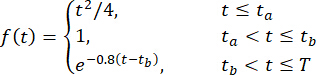 (30)
(30)
Dabei 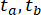 nimmst du 2 bzw. 16 s.
nimmst du 2 bzw. 16 s.
Der Mittelwert und die Standardabweichung der stochastischen seismischen Bodenbewegung sowie eine Zeitgeschichte der repräsentativen seismischen Bodenbewegung sind in Abbildung 3 dargestellt. Die Amplitude des Mittelwerts (0,06 m/s2) betrug ~8% der Amplitude der Standardabweichung (0,8 m/s2), was darauf hindeutet, dass das physikalisch motivierte stochastische Bodenbewegungsmodell die Eigenschaft des Mittelwerts Null aufwies. In der Zwischenzeit zeigte die seismische Bodenbewegung bemerkenswerte nicht-stationäre Verhaltensweisen sowohl im zeitlichen als auch im Frequenzbereich.
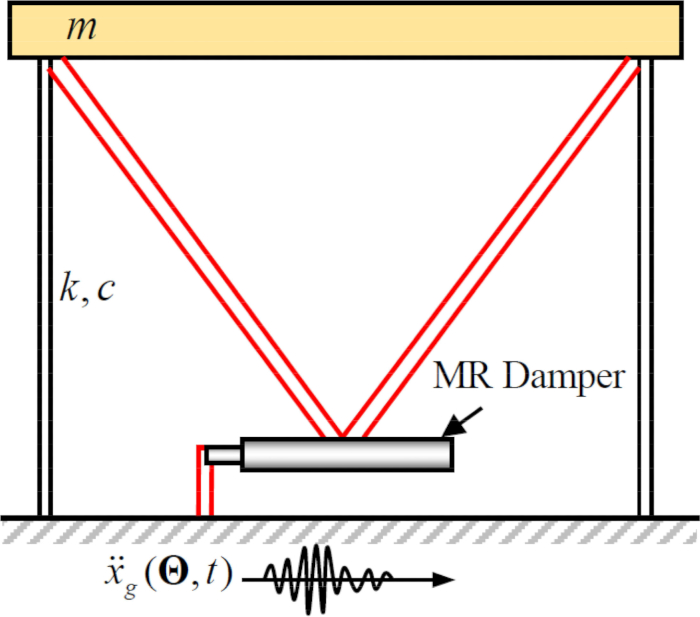
Abbildung 2: Skizze eines einstöckigen Schubrahmens mit magnetorheologischem Dämpfer.  bezeichnen die Strukturmasse, das Dämpfungsverhältnis und die Steifigkeit;
bezeichnen die Strukturmasse, das Dämpfungsverhältnis und die Steifigkeit; 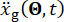 bezeichnet die stochastische seismische Anregung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
bezeichnet die stochastische seismische Anregung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
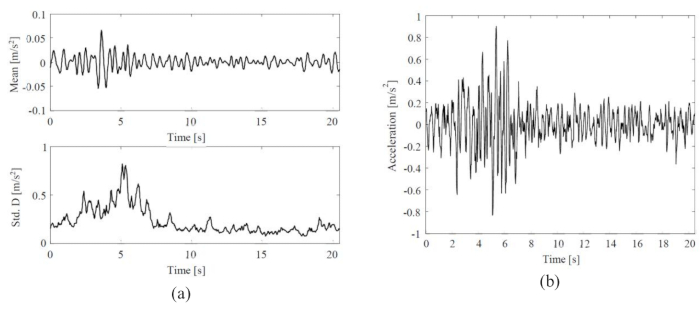
Abbildung 3: Statistiken und repräsentative Stichproben ausgewählter seismischer Bodenbewegungen. (A) Mittelwert und Standardabweichung der stochastischen seismischen Bodenbewegung; (B) Zeitverlauf repräsentativer seismischer Bodenbewegungen. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
2.1 Einflussanalyse der Zeitverzögerung
Um den Einfluss der Zeitverzögerung auf die semiaktive Regeleffektivität eines MRT-Dämpfers zu analysieren, zeigt Abbildung 4 die Verschiebungs-, Geschwindigkeits- und Beschleunigungseffektivität (Root-Mean-Square-Response) der kontrollierten Struktur. Das Gewichtungsmatrixverhältnis und die Dämpferparameter waren 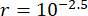 ,
, 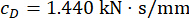 und
und 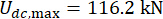 , was die optimierten Ergebnisse ohne Zeitverzögerungdarstellt 38. Die Reaktionen der kontrollierten Struktur mit Zeitverzögerung waren größer als die der kontrollierten Struktur ohne Zeitverzögerung, und der Einfluss der Zeitverzögerung auf den Kontrolleffekt stellte die Periodizität zusammen mit der Zunahme der Zeitverzögerung dar. Da es sich bei der semi-aktiven Kontrollmethode mit einem MR-Dämpfer um eine Art Rückkopplungsmethode handelt, wurde die Periodizität des Einflusses als mit der natürlichen Periode der kontrollierten Struktur (T = 0,56 s) in Beziehung gesetzt.
, was die optimierten Ergebnisse ohne Zeitverzögerungdarstellt 38. Die Reaktionen der kontrollierten Struktur mit Zeitverzögerung waren größer als die der kontrollierten Struktur ohne Zeitverzögerung, und der Einfluss der Zeitverzögerung auf den Kontrolleffekt stellte die Periodizität zusammen mit der Zunahme der Zeitverzögerung dar. Da es sich bei der semi-aktiven Kontrollmethode mit einem MR-Dämpfer um eine Art Rückkopplungsmethode handelt, wurde die Periodizität des Einflusses als mit der natürlichen Periode der kontrollierten Struktur (T = 0,56 s) in Beziehung gesetzt.
Verglichen mit den Reaktionen der unkontrollierten Struktur, bei denen die maximale MRS-Verschiebung, -Geschwindigkeit und -Beschleunigung 24,6 mm, 270,0 mm/s und 3111,3 mm/s2 betrugen, erzielte die MR-Dämpfer-gesteuerte Struktur einen bemerkenswerten Effekt. Im Gegensatz zur Instabilität der aktiv kontrollierten Struktur mit Zeitverzögerung25 erzielte das auf MR-Dämpfern basierende semiaktive Kontrollverfahren auch mit Zeitverzögerung noch eine gewisse Wirkung.

Abbildung 4: Die maximalen mittleren Quadrate der Antworten der kontrollierten Struktur im Laufe der Zeit. a) Verdrängung; (b) Geschwindigkeit; (c) Beschleunigung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Um den Einfluss der Zeitverzögerung auf die Zuverlässigkeit einer semi-aktiv gesteuerten Struktur zu analysieren, zeigt Abbildung 5 die Zuverlässigkeit von Verschiebung, Geschwindigkeit und Beschleunigung mit zunehmender Zeitverzögerung. Die Reliabilität der Antworten der kontrollierten Struktur mit Zeitverzögerung war niedriger als die Werte ohne Zeitverzögerung, was bedeutet, dass die Zuverlässigkeit der kontrollierten Struktur durch die Zeitverzögerung verringert wurde. Ähnlich wie beim maximalen RMS zeigte der Effekt der Zuverlässigkeitskontrolle eine Periodizität mit zunehmender Zeitverzögerung. Darüber hinaus war die Zuverlässigkeit der kontrollierten Struktur, mit oder ohne Zeitverzögerung, höher als die Werte unkontrollierter Strukturen mit der Zuverlässigkeit von Verschiebung, Geschwindigkeit und Beschleunigung von 0,0954, 0,1058 und 0,1111.
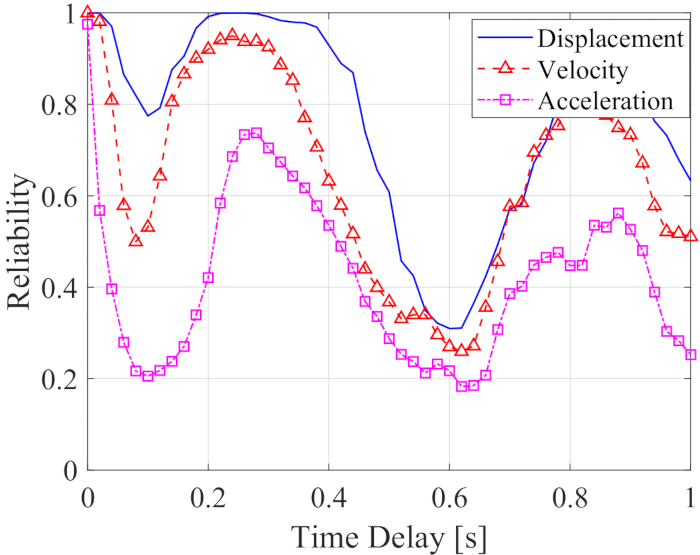
Abbildung 5: Zuverlässigkeit der kontrollierten Struktur der Antworten mit zunehmender Zeitverzögerung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Zusammenfassend lässt sich sagen, dass die Reaktionen der Struktur durch die semiaktive Kontrollmethode abgeschwächt wurden. Die Wirksamkeit der Kontrolle, unabhängig vom RMS oder der Zuverlässigkeit, der semiaktiven Regelungsmethode wurde jedoch durch die Zeitverzögerung verringert. Daher ist es notwendig, die Zeitverzögerung zu kompensieren.
2.1.1 Analyse des Verfahrens zur Kompensation von Zeitverzögerungen
Zur Analyse der Wirksamkeit des vorgeschlagenen Zeitverzögerungskompensationsverfahrens werden in Abbildung 6 die RMS-Zeitverläufe von Verschiebung, Geschwindigkeit und Beschleunigung für unkontrollierte (Unc), zeitverzögerte Systeme mit nicht kompensationsgesteuerter (TDN-SAC-PSO) und zeitverzögerte Systeme mit kontrollierter Kompensation (TDC-SAC-PSO) verglichen, wobei die Zeitverzögerung 0,1 s betrug. Die Parameter der Gewichtungsmatrix und der semiaktiven Kontrollmethode sind die gleichen wie in Schritt 2.1.

Abbildung 6: Vergleich der Root-Mean-Square-Time-History-Historie von Strukturen, die mit verschiedenen Methoden gesteuert werden. a) Verdrängung; (b) Geschwindigkeit; (c) Beschleunigung; (D) Kontrollgewalt. Abkürzungen: Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; TDN -SAC-PSO = zeitverzögertes System mit nicht-kompensierter Steuerung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Beide Kontrollmethoden verringerten die Reaktionen der Struktur im Vergleich zur unkontrollierten Struktur signifikant, was die Vorteile der MR-Dämpfer-basierten Kontrollmethode aufzeigt. Im Vergleich zur unkontrollierten Struktur wird der maximale Effektivwert von Verschiebung, Geschwindigkeit und Beschleunigung mit der TDN-SAC-PSO-Methode um 75,79 %, 73,75 % und 61,22 % verringert. Darüber hinaus werden mit der Zeitverzögerungskompensation die Reaktionen der kontrollierten Struktur um 82,59 %, 80,40 % und 73,04 % mit der TDC-SAC-PSO-Methode verringert. Der maximale Effektivwert der Steuerkraft mit der TDC-SAC-PSO-Methode verringerte sich im Vergleich zur TDN-SAC-PSO-Methode um 8,43 %, obwohl die Schwingungsreaktionen der erstgenannten Methode geringer waren als bei der letzteren. Die obige Analyse zeigt, dass der Einfluss der Zeitverzögerung auf das MR-Dämpfer-basierte Kontrollverfahren durch das Kompensationsverfahren effektiv verringert wurde, was die Notwendigkeit einer Zeitverzögerungskompensation für das semiaktive MR-Dämpfer-Kontrollverfahren zeigt.

Abbildung 7: PDF-Vergleich zu typischen Zeitpunkten von Strukturantworten. a) Verdrängung; (b) Geschwindigkeit; (c) Beschleunigung. Abkürzungen: PDF = Wahrscheinlichkeitsdichtefunktion; Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; TDN -SAC-PSO = zeitverzögertes System mit nicht-kompensierter Steuerung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Um die Auswirkungen der vorgeschlagenen Kompensationsmethode auf die Unsicherheit der Reaktionen der kontrollierten Struktur umfassend aufzuzeigen, sind in Abbildung 7 die Vergleiche der Wahrscheinlichkeitsdichtefunktion (PDF) von Verschiebung, Geschwindigkeit und Beschleunigung zu typischen Zeiten (3, 7 und 11 s) dargestellt. Die PDFs für die TDN-SAC-PSO-Methode waren schmaler als die der Unkontrollierten Struktur, was bedeutet, dass die Unsicherheit der Strukturantworten durch die semi-aktive Kontrollmethode auch mit Zeitverzögerung verringert wurde. Als die Zeitverzögerung kompensiert wurde, wurden die PDFs der Antworten weiter eingegrenzt. Daher ist die vorgeschlagene Kompensationsmethode notwendig, um den semiaktiven Kontrolleffekt zu verbessern.
| Steuerungsmethode | Verschiebung | Geschwindigkeit | Beschleunigung | Kontrollkraft | Mindestwert |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| TDN-SAC-PSO | 0.7747 | 0.531 | 0.2054 | 0.884 | 0.2054 |
Tabelle 1: Schwingungsverhalten und Zuverlässigkeit der Steuerkraft von Strukturen, die mit verschiedenen Methoden gesteuert werden. Abkürzungen: Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; TDN -SAC-PSO = zeitverzögertes System mit nicht-kompensierter Steuerung.
Das Schwingungsverhalten und die Zuverlässigkeit der Steuerkraft von unkontrollierten, TDC-SAC-PSO- und TDN-SAC-PSO-Methoden kontrollierten Strukturen sind in Tabelle 1 dargestellt. Mit der TDN-SAC-PSO Methodenkontrolle wurde die Zuverlässigkeit der Struktur im Vergleich zur unkontrollierten Struktur drastisch erhöht, was die Wirksamkeit der MRT-Dämpfer-basierten Kontrollmethode auch mit der Zeit bestätigt. Mit der Zeitverzögerungskompensation wurde jedoch die Zuverlässigkeit im Vergleich zu ohne Kompensation deutlich erhöht, insbesondere bei der Beschleunigung. Bemerkenswert ist auch, dass die Zuverlässigkeit der verschiedenen Antworten und die Kontrollkraft für die TDC-SAC-PSO-Methode signifikante Unterschiede aufwiesen. Dies deutet darauf hin, dass die optimalen Werte kritischer Parameter für die Regelung ohne Zeitverzögerung für die Regelung mit Zeitverzögerung nicht optimal sind. Um die optimale Regelwirkung des Schwingungsverhaltens und der Regelkraft mit Zeitverzögerungseinfluss zu erzielen, müssen die Parameter weiter optimiert werden. Basierend auf der obigen Analyse wird der Schluss gezogen, dass die semiaktive Regelungsmethode mit einem MR-Dämpfer die Schwingungsreaktionen der Struktur effektiv verringern kann, während die Parameter aufgrund des Einflusses der Zeitverzögerung optimiert werden müssen.
2.2 Optimierung der Parameter
Um die optimalen Werte der Parameter zu erreichen, wurde die integrierte Optimierungsmethode auf der Grundlage des Zuverlässigkeitskriteriums38 angewendet. Die Optimierung kritischer Parameter erfolgte mit  ,
, 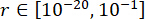 ,
, 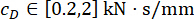 ,
, 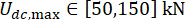 und den Abstimmzeiten der MR-Dämpferkraft s = 8. Für die Umsetzung der Optimierung wurde die GA-Toolbox innerhalb von MATLAB verwendet.
und den Abstimmzeiten der MR-Dämpferkraft s = 8. Für die Umsetzung der Optimierung wurde die GA-Toolbox innerhalb von MATLAB verwendet.
Die Optimierungsergebnisse der Parameter sind 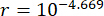 ,
, 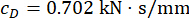 und
und  für die Zeitverzögerung
für die Zeitverzögerung  . Abbildung 8 zeigt die RMS-Zeitverläufe von Verschiebung, Geschwindigkeit, Beschleunigung und Steuerkraft für die unkontrollierten (Unc), TDC-SAC-PSO-Methode und SOSC-PSO-Methode-kontrollierten Strukturen. Das SOSC-PSO-Verfahren bezeichnet das semiaktive Regelungsverfahren mit Zeitverzögerungskompensation und optimierten kritischen Parameterwerten.
. Abbildung 8 zeigt die RMS-Zeitverläufe von Verschiebung, Geschwindigkeit, Beschleunigung und Steuerkraft für die unkontrollierten (Unc), TDC-SAC-PSO-Methode und SOSC-PSO-Methode-kontrollierten Strukturen. Das SOSC-PSO-Verfahren bezeichnet das semiaktive Regelungsverfahren mit Zeitverzögerungskompensation und optimierten kritischen Parameterwerten.

Abbildung 8: RMS-Zeitverläufe von Verschiebung, Geschwindigkeit, Beschleunigung und Steuerkraft für unkontrollierte und nach der TDC-SAC-PSO-Methode und SOSC-PSO-Methode kontrollierte Strukturen. a) Verdrängung; (b) Geschwindigkeit; (c) Beschleunigung; (D) Kontrollgewalt. Abkürzungen: Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; SOSC-PSO = Stochastische optimale semiaktive Regelungsmethode mit Zeitverzögerungskompensation. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Aus Abbildung 8 ist ersichtlich, dass die Kontrolleffekte der TDC-SAC-PSO- und SOSC-PSO-Methoden kaum einen Unterschied zeigten. Der maximale Effektivwert der Verschiebungsgeschwindigkeit und -beschleunigung betrug bei der ersten Methode 81,60 %, 81,21 %, 73,62 % für die unkontrollierte Struktur und 82,59 %, 80,40 %, 73,04 % für die zweite Methode. Um die Wahrscheinlichkeitseigenschaften der Reaktionen für beide Kontrollmethoden umfassend zu analysieren, zeigt Abbildung 9 die PDFs von Verschiebung, Geschwindigkeit und Beschleunigung für die unkontrollierten, TDC-SAC-PSO-Methoden- und SOSC-PSO-Methodenkontrollierten Strukturen. Beide Steuerungsmethoden hatten zu typischen Zeiten fast die gleichen PDFs von Verschiebung und Geschwindigkeit. Die Beschleunigungs-PDFs der SOSC-PSO-Methode waren schmaler als die der TDC-SAC-PSO-Methode, was bedeutet, dass die Unsicherheit der Beschleunigung bei der erstgenannten Methode einen besseren Kontrolleffekt erzielte.
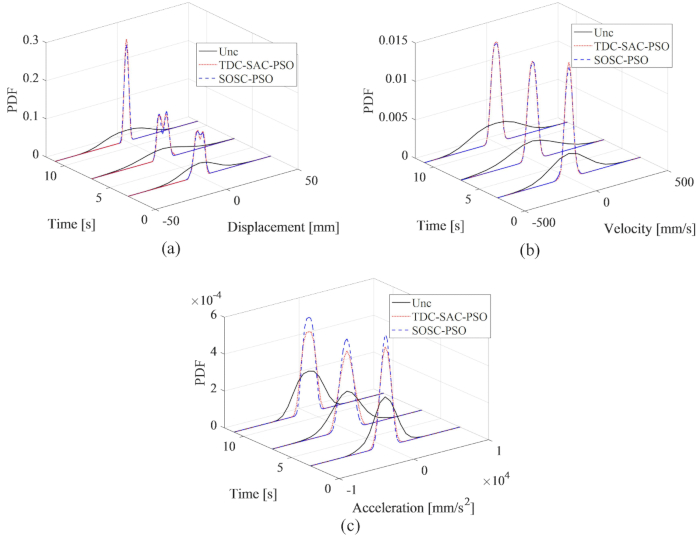
Abbildung 9: PDFs-Vergleich von Verschiebung, Geschwindigkeit und Beschleunigung für verschiedene kontrollierte Strukturen. a) Verdrängung; (b) Geschwindigkeit; (c) Beschleunigung. Abkürzungen: PDFs = Wahrscheinlichkeitsdichtefunktionen; Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; SOSC-PSO = Stochastische optimale semiaktive Regelungsmethode mit Zeitverzögerungskompensation. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Die Zuverlässigkeit von Weg, Geschwindigkeit, Beschleunigung und Steuerkraft für die ungeregelten und TDC-SAC-PSO- und SOSC-PSO-gesteuerten Strukturen ist in Tabelle 2 dargestellt. Beide Regelungsmethoden erreichten eine signifikante Steigerung der Zuverlässigkeit im Vergleich zur unkontrollierten Struktur. Die Verschiebungszuverlässigkeit unterschied sich kaum zwischen den TDC-SAC-PSO- und SOSC-PSO-Methoden. Während die Beschleunigungszuverlässigkeit, die geringste Zuverlässigkeit der geregelten Struktur, eine spürbare Steigerung erzielte. Das bedeutet, dass die SOSC-PSO-Methode den optimalen Kontrolleffekt erzielt.
| Steuerungsmethode | Verschiebung | Geschwindigkeit | Beschleunigung | Kontrollkraft | Mindestwert |
| Unc | 0.0954 | 0.1058 | 0.1111 | -- | 0.1111 |
| TDC-SAC-PSO | 0.9565 | 0.8107 | 0.7654 | 0.9845 | 0.7654 |
| SOSC-PSO | 0.953 | 0.8704 | 0.8934 | 0.9586 | 0.8934 |
Tabelle 2: Zuverlässigkeit für Strukturen, die mit verschiedenen Methoden gesteuert werden. Abkürzungen: Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; SOSC-PSO = Stochastische optimale semiaktive Regelungsmethode mit Zeitverzögerungskompensation.
Die Wirksamkeit der vorgeschlagenen SOSC-PSO-Methode mit Zeitverzögerung  wurde analysiert. Um das vorgeschlagene Verfahren für verschiedene Zeitverzögerungen weiter zu verifizieren, zeigt Tabelle 3 die optimalen Parameterwerte und die entsprechende Zuverlässigkeit für den Zeitverzögerungsbereich
wurde analysiert. Um das vorgeschlagene Verfahren für verschiedene Zeitverzögerungen weiter zu verifizieren, zeigt Tabelle 3 die optimalen Parameterwerte und die entsprechende Zuverlässigkeit für den Zeitverzögerungsbereich  .
.
| tD(s) | LG(R*) | CD(kN·s/mm) | U dc,max (kN) | Verschiebung | Geschwindigkeit | Beschleunigung | Kontrollkraft |
| 0 | -2.524 | 1.44 | 116.163 | 0.9997 | 0.9998 | 0.9752 | 1 |
| 0.02 | -4.413 | 0.414 | 144.066 | 0.9989 | 0.9988 | 0.872 | 0.9011 |
| 0.04 | -4.416 | 0.25 | 141.759 | 0.9998 | 0.9846 | 0.8881 | 0.9135 |
| 0.06 | -3.226 | 0.203 | 145.613 | 0.993 | 0.9318 | 0.8756 | 0.9556 |
| 0.08 | -5.207 | 0.345 | 133.692 | 0.9646 | 0.8998 | 0.8998 | 0.953 |
| 0.1 | -4.669 | 0.702 | 130.739 | 0.9531 | 0.8704 | 0.8934 | 0.9586 |
| 0.12 | -4.895 | 0.833 | 69.72 | 0.9526 | 0.863 | 0.888 | 0.9686 |
| 0.14 | -4.231 | 0.921 | 75.221 | 0.9531 | 0.8681 | 0.8697 | 0.9671 |
| 0.16 | -5.594 | 0.662 | 138.922 | 0.9529 | 0.8461 | 0.8262 | 0.931 |
| 0.18 | -4.262 | 0.882 | 76.335 | 0.9516 | 0.7873 | 0.7614 | 0.9618 |
| 0.2 | -3.926 | 0.783 | 67.951 | 0.904 | 0.7277 | 0.7116 | 0.9653 |
| 0.22 | -5.965 | 1.071 | 52.554 | 0.8377 | 0.6411 | 0.6205 | 0.965 |
| 0.24 | -4.481 | 1.216 | 128.148 | 0.7567 | 0.474 | 0.474 | 0.9687 |
| 0.26 | -3.53 | 0.672 | 53.706 | 0.53 | 0.4096 | 0.4158 | 0.9921 |
| 0.28 | -4.433 | 0.638 | 64.225 | 0.3547 | 0.3745 | 0.3464 | 0.9928 |
| 0.3 | -3.536 | 0.459 | 57.705 | 0.2735 | 0.316 | 0.2736 | 0.9929 |
| Unc | -- | -- | -- | 0.0954 | 0.1058 | 0.1111 | -- |
Tabelle 3: Die optimalen Parameterwerte und die entsprechenden Zuverlässigkeitswerte für verschiedene Zeitverzögerungen. 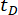 bezeichnet Zeitverzögerung;
bezeichnet Zeitverzögerung; 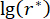 bezeichnen den optimalen logarithmischen Wert von r,r bezeichnet die Gewichtungsmatrix des Kontrollkoeffizienten;
bezeichnen den optimalen logarithmischen Wert von r,r bezeichnet die Gewichtungsmatrix des Kontrollkoeffizienten; 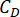 bezeichnet den viskosen Dämpfungskoeffizienten des MR-Dämpfers;
bezeichnet den viskosen Dämpfungskoeffizienten des MR-Dämpfers; 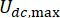 bezeichnen die maximalen und minimalen Coulomb-Kräfte des MR-Dämpfers.
bezeichnen die maximalen und minimalen Coulomb-Kräfte des MR-Dämpfers.
Es ist zu beobachten, dass die Zuverlässigkeit von Verschiebung, Geschwindigkeit und Beschleunigung im Vergleich zur unkontrollierten Struktur verbessert wurde, selbst bei Vorhandensein von Zeitverzögerungen, was die Robustheit der vorgeschlagenen Methode gegenüber solchen Verzögerungen demonstriert. Die Zuverlässigkeit der strukturellen Reaktionen mit der vorgeschlagenen Kontrollmethode nahm jedoch mit zunehmender Zeitverzögerung ab, was darauf hindeutet, dass die Auswirkungen der Zeitverzögerung auf die Wirksamkeit der Kontrolle zwar gemildert, aber nicht vollständig eliminiert werden können. Bemerkenswert ist, dass die Zuverlässigkeit der Steuerkraft über verschiedene Zeitverzögerungen hinweg über 90 % hinweg blieb.
3. Numerisches Beispiel
Um die vorgeschlagene SOSC-PSO-Methode in der MDOF-Struktur zu verifizieren, wurde eine sechsstöckige Struktur mit zwei MR-Dämpfern analysiert, die im ersten und dritten Obergeschoss installiert waren, wie in Abbildung 10 gezeigt. Die seismischen Proben, die mit dem stochastischen seismischen Modell in Abschnitt 2 erzeugt wurden, wurden angewendet, und die Zuverlässigkeitsschwellen für Verschiebung, Geschwindigkeit, Beschleunigung und Steuerkraft betrugen 20 mm, 200 mm/s, 3.000 mm/s2 und 200 kN. Gl. (27) wurden als Gewichtungsmatrix mit  verwendet. Die GA-Toolbox von MATLAB wurde verwendet, um ,
verwendet. Die GA-Toolbox von MATLAB wurde verwendet, um ,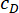 und , mit optimalen Bereichen
und , mit optimalen Bereichen 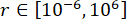 ,
, 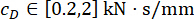 und
und 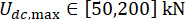 zu optimieren
zu optimieren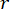
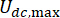 .
.

Bild 10: Sechsgeschossiger Aufbau mit zwei MR-Dämpfern. Abkürzung: MR = magnetorheologisch. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
3.1 Einflussanalyse der Zeitverzögerung
Um den Einfluss der Zeitverzögerung auf die Kontrolleffektivität des MR-Dämpfers in der MDOF-Struktur zu analysieren, zeigt Abbildung 11 den maximalen Effektivwert der Verschiebung (Verschiebung zwischen den Stockwerken), der Geschwindigkeit (Geschwindigkeit zwischen den Stockwerken) und der Beschleunigung (Geschossbeschleunigung) zusammen mit der Zeitverzögerung für die TDC-SAC-PSO-Methode. Die Parameter waren 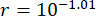 ,
, , und
, und 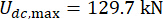 für den MR-Dämpfer im 1. Obergeschoss;
für den MR-Dämpfer im 1. Obergeschoss;  und
und 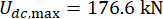 für den MR-Dämpfer im 3. Obergeschoss, was die optimierten Ergebnisse ohne Zeitverzögerung sind. Die maximale RMS der kontrollierten Strukturantworten zeigte Periodenfluktuation zusammen mit Zeitverzögerung. Die maximale RMS von Verschiebung und Geschwindigkeit lag im 1. Stockwerk, die maximale Beschleunigung im 6. Stockwerk. Außerdem waren alle maximalen MRS von Reaktionen mit Zeitverzögerung größer als die Werte ohne Zeitverzögerung, was bedeutet, dass die Zeitverzögerung den Kontrolleffekt des MR-Dämpfers verringert.
für den MR-Dämpfer im 3. Obergeschoss, was die optimierten Ergebnisse ohne Zeitverzögerung sind. Die maximale RMS der kontrollierten Strukturantworten zeigte Periodenfluktuation zusammen mit Zeitverzögerung. Die maximale RMS von Verschiebung und Geschwindigkeit lag im 1. Stockwerk, die maximale Beschleunigung im 6. Stockwerk. Außerdem waren alle maximalen MRS von Reaktionen mit Zeitverzögerung größer als die Werte ohne Zeitverzögerung, was bedeutet, dass die Zeitverzögerung den Kontrolleffekt des MR-Dämpfers verringert.

Abbildung 11: Maximaler Effektivwert der Antworten zusammen mit der Zeitverzögerung für die TDC-SAC-PSO-Methode-gesteuerte Struktur. a) Verdrängung; (b) Geschwindigkeit; (c) Beschleunigung. Abkürzungen: RMS = Wurzel-Mittelwert-Quadrat; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Die Zuverlässigkeit von Verschiebung, Geschwindigkeit und Beschleunigung zusammen mit der Zeitverzögerung ist in Abbildung 12 dargestellt. Die Zuverlässigkeit von Geschwindigkeit und Beschleunigung zeigt eine Periodenfluktuation zusammen mit der Zeitverzögerung, während die Zuverlässigkeit der Verschiebung zusammen mit der Zeitverzögerung dramatisch abnahm; Alle Zuverlässigkeitswerte waren zu jedem Zeitpunkt mit Zeitverzögerung geringer als die ohne Zeitverzögerung. Daher ist das Verfahren zur Kompensation der Zeitverzögerung notwendig, um den Einfluss der Zeitverzögerung auf die Zuverlässigkeit der MR-Dämpfer-gesteuerten Struktur zu reduzieren.
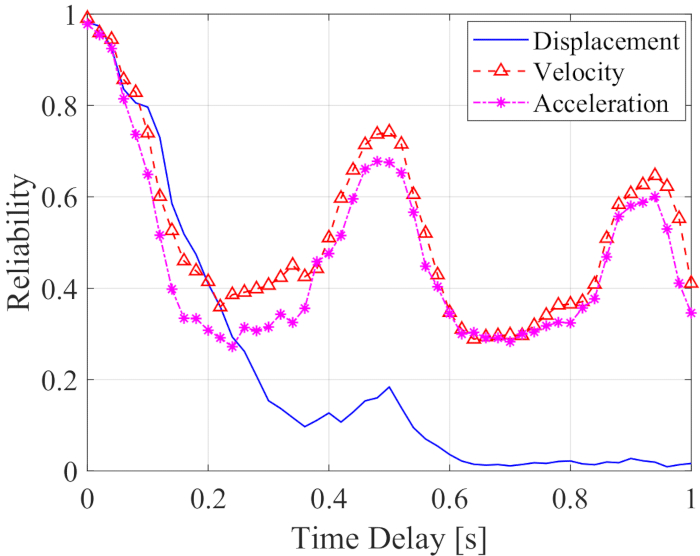
Abbildung 12: Zuverlässigkeit der Reaktionen der kontrollierten Struktur zusammen mit der Zeitverzögerung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
3.2 Kontrollwirkung der Zeitverzögerungskompensation
Basierend auf der vorgeschlagenen TDC-SAC-PSO Methode wurde die 6-DOF-Struktur mit zwei MR-Dämpfern analysiert. Abbildung 13 zeigt die RMS-Zeitverläufe von Verschiebung und Beschleunigung im 1. und 3. Geschoss für die unkontrollierten (Unc), TDC-SAC-PSO-gesteuerten und TDN-SAC-PSO Methodengesteuerten Strukturen. Die Zeitverzögerung betrug 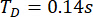 , und das Verhältnis
, und das Verhältnis 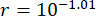 der Gewichtungsmatrix, die MR-Dämpferparameter waren
der Gewichtungsmatrix, die MR-Dämpferparameter waren 
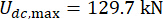 für das 1. Obergeschoss und
für das 1. Obergeschoss und 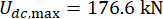 für das 3. Obergeschoss
für das 3. Obergeschoss  .
.

Abbildung 13: RMS-Zeitverläufe von Verschiebungen und Beschleunigungen im 1. und 3. Obergeschoss für Strukturen, die mit unterschiedlichen Methoden gesteuert wurden. (A) Verschiebung im 1. Stock; (B) Verschiebung im 3. Stock; (C) Beschleunigung im 1. Stock; (D) Beschleunigung im 3. Stock. Abkürzungen: RMS = Wurzel-Mittelwert-Quadrat; Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; TDN -SAC-PSO = zeitverzögertes System mit nicht-kompensierter Steuerung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Der maximale Effektivwert der Verschiebung im 1. und 3. Obergeschoss wurde durch die TDN-SAC-PSO-Methode, bei der die Zeitverzögerung nicht kompensiert wurde, um 35,42 % bzw. 30,44 % reduziert. Mit Kompensation wurde der maximale RMS der Verschiebung im 1. und 3. Obergeschoss um 49,33 % bzw. 53,39 % reduziert. Ohne Kompensation stieg der maximale Effektivwert der Beschleunigung im 1. und 3. Obergeschoss um 16,22 % bzw. 2,88 %, sank jedoch um 25,77 % bzw. 36,00 % mit Kompensation. Daher ist die Kompensation der Zeitverzögerung bei der MR-Dämpferregelung notwendig, um die Reaktionen der Struktur, insbesondere der Beschleunigung, zu reduzieren.
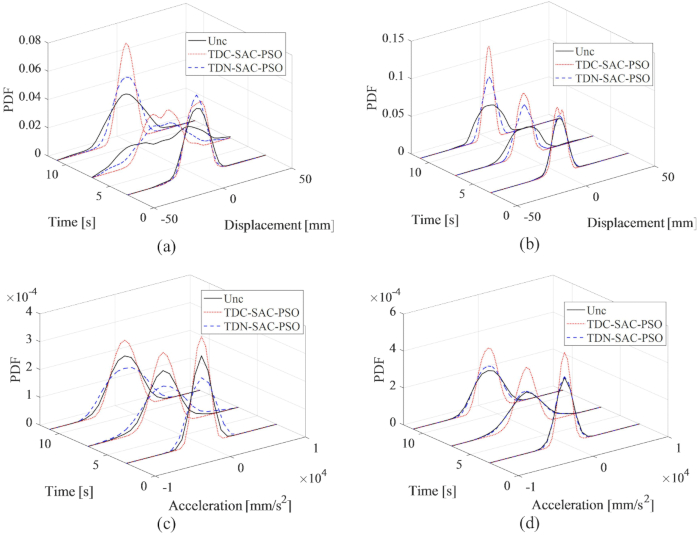
Abbildung 14: PDFs von Verschiebung und Beschleunigung im 1. und 3. Stock für verschiedene Steuerungsmethoden. (A) Verschiebung im 1. Stock; (B) Verschiebung im 3. Stock; (C) Beschleunigung im 1. Stock; (D) Beschleunigung im 3. Stock. Abkürzungen: PDFs = Wahrscheinlichkeitsdichtefunktionen; Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; TDN -SAC-PSO = zeitverzögertes System mit nicht-kompensierter Steuerung. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Die PDFs der Verschiebung und Beschleunigung im 1. und 3. Obergeschoss sind in Abbildung 14 dargestellt und zeigen die unterschiedlichen Kontrolleffekte der Methoden TDC-SAC-PSO und TDN-SAC-PSO im Vergleich zur unkontrollierten Struktur. Ohne Kompensation waren die PDFs der Verschiebung im 1. und 3. Obergeschoss immer noch schmaler als die des unkontrollierten Baukörpers. Darüber hinaus wurden mit der Kompensation der Zeitverzögerung die PDFs der Verschiebung schmaler als die der TDN-SAC-PSO Methode-gesteuerten Struktur. Im Gegensatz zur Verschiebung ohne Kompensation waren die PDFs der Beschleunigung im 1. Stock für die TDN-SAC-PSO-Methode breiter als die der unkontrollierten Struktur. Mit Kompensation waren die Beschleunigungsmomente sowohl im 1. als auch im 3. Stock jedoch schmaler als die der unkontrollierten Struktur. Damit wird die Notwendigkeit einer Zeitverzögerungskompensation für die Erhöhung der Sicherheit des Strukturverhaltens, insbesondere für die Beschleunigung, verifiziert.
| Steuerungsmethode | Verschiebung | Geschwindigkeit | Beschleunigung | Kontrollkraft im 1. Stock | Kontrolltruppe im 3. Stock |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDN-SAC-PSO | 0.5851 | 0.5258 | 0.398 | 1 | 1 |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
Tabelle 4: Zuverlässigkeit für Strukturen, die mit verschiedenen Methoden gesteuert werden. Abkürzungen: Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; TDN -SAC-PSO = zeitverzögertes System mit nicht-kompensierter Steuerung.
Die Zuverlässigkeitswerte von Verschiebung, Geschwindigkeit, Beschleunigung und Steuerkraft mit den Struktursystemen, die mit den verschiedenen Methoden gesteuert werden, sind in Tabelle 4 dargestellt. Die Zuverlässigkeitswerte der Strukturantworten wurden mit der äquivalenten Extremwertmethode25 berechnet. Durch die Regelung der TDN-SAC-PSO-Methode stieg die Zuverlässigkeit der Verschiebung im Vergleich zur unkontrollierten Struktur, während die Zuverlässigkeit von Geschwindigkeit und Beschleunigung abnahm. Mit der Zeitverzögerungskompensation im TDC-SAC-PSO-Verfahren wurde die Zuverlässigkeit von Weg, Geschwindigkeit und Beschleunigung deutlich erhöht. Darüber hinaus werden die Zuverlässigkeitswerte der Steuerkraft sowohl für die TDN-SAC-PSO- als auch für die TDN-SAC-PSO-Methoden ausreichend eingehalten. Somit erzielt das vorgeschlagene Verfahren zur Kompensation der Zeitverzögerung einen günstigen Kontrolleffekt für die MR-Dämpfer-gesteuerte Struktur.
3.3 Optimierung der Parameter
Um den optimalen Regelungseffekt zu erzielen, wurden die Parameter des vorgeschlagenen Regelungsverfahrens auf der Grundlage des Zuverlässigkeitskriteriums optimiert. Mit der Zeitverzögerung 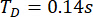 war
war 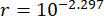 das optimale Ergebnis ;
das optimale Ergebnis ; 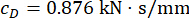 , und
, und  für den MR-Dämpfer
für den MR-Dämpfer 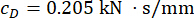 des 1. Stockwerks und
des 1. Stockwerks und 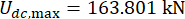 für den 3. MR-Dämpfer.
für den 3. MR-Dämpfer.
Die RMS-Zeitverläufe von Verschiebung und Beschleunigung im 1. und 3. Geschoss sind in Abbildung 15 dargestellt, in der die Kontrolleffekte der TDC-SAC-PSO- und SOSC-PSO-Methoden und der unkontrollierten Struktur verglichen werden. Mit der MR-Dämpferregelung, mit oder ohne Zeitverzögerungskompensation, sank der Effektivwert von Verschiebung und Beschleunigung erheblich. Mit der SOSC-PSO-Methode verringerte sich der maximale Effektivwert der Verschiebung im 1. und 3. Obergeschoss um 65,15 % bzw. 63,16 % im Vergleich zur unkontrollierten Struktur. Im Vergleich zur TDC-SAC-PSO-Methode wurde das Verschiebungsverhalten weiter reduziert. Der maximale Effektivwert der Beschleunigung im 1. und 3. Obergeschoss wird um 23,39 % bzw. 35,60 % für die SOSC-PSO-Methode verringert. Es gab kaum Unterschiede in der Kontrollwirkung der Beschleunigung für die SOSC-PSO- und TDC-SAC-PSO-Methoden, was darauf hindeutet, dass die Kontrollwirkung der Zeitverzögerungskompensation für Verschiebung und Beschleunigung unterschiedlich war.
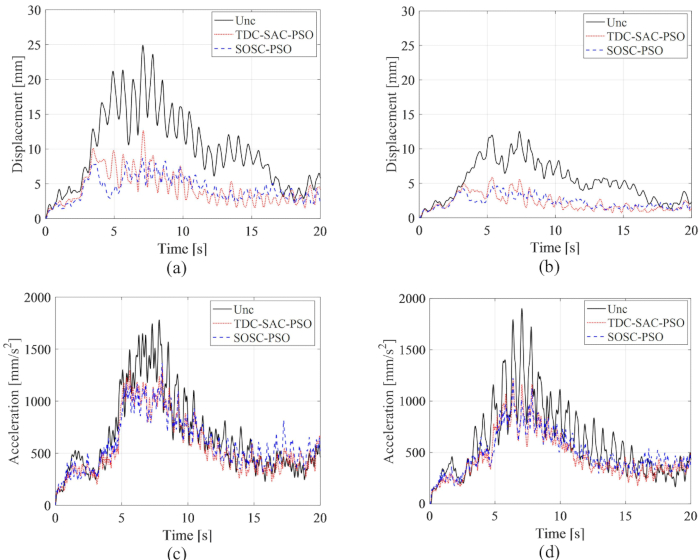
Abbildung 15: RMS-Zeitverläufe von Verschiebung und Beschleunigung im 1. und 3. Stock für verschiedene Regelungsmethoden. (A) Verschiebung im 1. Stock; (B) Verschiebung im 3. Stock; (C) Beschleunigung im 1. Stock; (D) Beschleunigung im 3. Stock. Abkürzungen: RMS = Wurzel-Mittelwert-Quadrat; Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; SOSC-PSO = Stochastische optimale semiaktive Regelungsmethode mit Zeitverzögerungskompensation. Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Die PDFs der Verschiebung und Beschleunigung im 1. und 3. Obergeschoss sind in Abbildung 16 dargestellt; Die PDFs der Verschiebung und Beschleunigung wurden durch die Methoden TDC-SAC-PSO und SOSC-PSO im Vergleich zur unkontrollierten Struktur eingegrenzt. Außerdem wurden die PDFs der Verschiebung und Beschleunigung für die SOSC-PSO-Methode im Vergleich zu denen der TDC-SAC-PSO Methode-kontrollierten Struktur weiter verengt. Daher erzielte das vorgeschlagene Regelungsverfahren zur Kompensation von Zeitverzögerungen bei der Parameteroptimierung eine bessere Regelungswirkung als ohne Optimierung.

Abbildung 16: PDFs von Verschiebung und Beschleunigung im 1. und 3. Stock für verschiedene Steuerungsmethoden. (A) Verschiebung im 1. Stock; (B) Verschiebung im 3. Stock; (C) Beschleunigung im 1. Stock; (D) Beschleunigung im 3. Stock. Abkürzungen: PDFs = Wahrscheinlichkeitsdichtefunktionen; Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; SOSC-PSO = Stochastische optimale semiaktive Regelungsmethode mit Zeitverzögerungskompensation Bitte klicken Sie hier, um eine größere Version dieser Abbildung anzuzeigen.
Die Zuverlässigkeitswerte für Weg, Geschwindigkeit, Beschleunigung und Steuerkraft sind in Tabelle 5 dargestellt. Die Reliabilitätswerte für die SOSC-PSO-Methode waren höher als die für die TDC-SAC-PSO-Methode. Währenddessen behielt die Steuerkraft immer noch eine ausreichende Zuverlässigkeit. Daher ist die Optimierung der Parameter notwendig, um den besten Regelungseffekt für das MR-Dämpfer-basierte Regelungsverfahren zu erzielen.
| Steuerungsmethode | Verschiebung | Geschwindigkeit | Beschleunigung | Kontrollkraft im 1. Stock | Kontrolltruppe im 3. Stock |
| Unc | 0.0114 | 0.5822 | 0.6372 | -- | -- |
| TDC-SAC-PSO | 0.806 | 0.8674 | 0.8037 | 1 | 1 |
| SOSC-PSO | 0.9544 | 0.9314 | 0.8788 | 1 | 1 |
Tabelle 5: Zuverlässigkeit für Strukturen, die mit verschiedenen Methoden gesteuert werden. Abkürzungen: Unc = unkontrolliert; TDC-SAC-PSO = zeitverzögertes System mit Kompensationssteuerung; SOSC-PSO = Stochastische optimale semiaktive Regelungsmethode mit Zeitverzögerungskompensation.
Ergebnisse
Mit dem Ziel des Einflusses der Zeitverzögerung auf die Kontrolleffektivität des MR-Dämpfer-basierten Verfahrens wird in diesem Beitrag ein semiaktives Regelungsverfahren mit Zeitverzögerungskompensation vorgeschlagen. In der vorgeschlagenen Methode werden die kritischen Parameter auf der Grundlage des Zuverlässigkeitskriteriums optimiert. Durch den Vergleich der Wirksamkeit der Kontrollen werden folgende Schlussfolgerungen gezogen:
(1) Die semiaktive Kon...
Diskussion
Mit der Einführung der physikalischen stochastischen optimalen Kontrolltheorie (PSO) wird in dieser Arbeit eine stochastische optimale semiaktive Kontrollmethode mit Zeitverzögerungskompensation (SOSC-PSO) vorgeschlagen, die darauf ausgelegt ist, die Zuverlässigkeit von Strukturen, die durch MR-Dämpfer gesteuert werden, zu erhalten. Um die Zeitverzögerung in dem vorgeschlagenen Verfahren zu kompensieren, wird die semiaktive Steuerkraft nicht nur als Funktion der gegenwärtigen Zust?...
Offenlegungen
Alle Autoren haben keine Interessenkonflikte anzugeben.
Danksagungen
Die Autoren danken der Naturwissenschaftlichen Stiftung der Provinz Hebei (Grant No. E2023210007).
Materialien
| Name | Company | Catalog Number | Comments |
| MATLAB | MathWorks | 2016 | Using for the calculation of the proposed method |
Referenzen
- Yao, J. T. P. Concept of structural control. J Struct Div. 98 (7), 1567-1574 (1972).
- Liu, J., Silva, C. E., Dyke, S. J., Wu, Y., Liu, H. Using real-time hybrid simulation for active mass damper experimentation and validation. Mech Mach Theory. 191, 105474 (2024).
- Pan, H., Li, C., Cao, L. Bidirectional pendulum-type tuned tendem mass dampers-inerters for integrated control of alongwind and crosswind responses in super-tall buildings. J Build Eng. 100, 111676 (2025).
- Housner, G. W. et al. Structural control: past, present, and future. J Eng Mech. 123 (9), 897-971 (1997).
- Rahman, M., Ong, Z. C., Chong, W. T., Julai, S. Smart Semi-active PID-ACO control strategy for tower vibration reduction in Wind Turbines with MR damper. Earthq Eng Eng Vib. 18 (4), 887-902 (2019).
- Morales-Beltran, M., Paul, J. Active and semi-active strategies to control building structures under large earthquake motion. J Earthquake Eng. 19 (7), 1086-1111 (2015).
- Shu, Z., You, R., Xie, Y. Viscoelastic dampers for vibration control of building structures: A state-of-art review. J Earthq Eng. 28 (12), 3558-3585 (2024).
- Soong, T. T. Active structural control: Theory and practice. Longman Scientific & Technical. New York (1990).
- Wan, H. P., Ma, Q., Dong, G. S., Luo, Y., Ni, Y. Q. Data-driven model reduction approach for active vibration control of cable-strut structures. Eng Struct. 302, 117434 (2024).
- Cao, L., Li, X., Huang, Y., Li, C., Pan, H. High robust eddy current tuned tandem mass dampers-inerters for structures under the ground acceleration. Soil Dyn Earthq Eng. 188, 109040 (2025).
- Chha, H., Peng, Y. Adaptive semiactive control of structure with magnetorheological dampers using wavelet packet transform. Adv Struct Eng. 27 (9), 1509-1527 (2024).
- Zeng, X., Peng, Y., Chen, J. Serviceability-based damping optimization of randomly wind-excited high-rise buildings. Struct Des Tall Spec. 26 (11), e1371 (2017).
- Li, C., Chang, K., Cao, L., Huang, Y. Performance of a nonlinear hybrid base isolation system under the ground motions. Soil Dyn Earthq Eng. 143, 106589 (2021).
- Cao, L., Li, C. A high performance hybrid passive base-isolated system. Struct Control Health Monitoring. 29 (3), e2887 (2022).
- Zareie, S., Issa, A. S., Seethaler, R., Zabihollah, A., Ahmad, R. A novel SMA-magnetorheological hybrid bracing system for seismic control. Eng Struct. 244, 112709 (2021).
- Chu, S. Y., Soong, T. T., Reinhorn, A. M. Active, hybrid and semi-active structural control. John Wiley & Sons, New York (2005).
- Danielian, S. A., Jabbari, F., Zareian, F. Effects and distribution of semi-active resettable springs on the seismic response of asymmetric structures. Earthq Eng Struct D. 52 (10). 2966-2982 (2023).
- Shuang, Z., Wenliuhan, H. S., Liu, Y. H., Inoue, N., Zhai, Z. P. Seismic response control for bridge piers with semi-active MR damper based on displacement feedback. J Earthq Eng. 28 (3). 849-865 (2024).
- Wang, Y., Dyke, S. Modal-based LQG for smart base isolation system design in seismic response control. Struct Control Health Monitoring. 20 (5), 753-768 (2013).
- Desai, R. M. et al. Performance evaluation of a single sensor control scheme using a twin-tube MR damper based semi-active suspension. J Vib Eng Technol. 9, 1193-1210 (2021).
- Abdi, M. S., Nekooei, M. Jafari, M. A. Seismic control of multi-degrees-of-freedom structures by vertical mass isolation method using MR dampers. Earthq Eng Eng Vib. 23 (2), 503-510 (2024).
- Bhowmik, K., Debnath, N. Semi-active vibration control of soft-storey building with magnetorheological damper under seismic excitation. J Vib Eng Technol. 12 (4), 6943-6961 (2024).
- Yang, J. N., Akbarpour, A., Askar, G. Effect of time delay on control of seismic-excited buildings. J Struct Eng. 116 (10), 2801-2814 (1990).
- Temimi, H., Ben-Romdhane, M., El-Borgi, S., Cha, Y. Time-delay effects on controlled seismically excited linear and nonlinear structures. Int J Struct Stab Dyn. 16 (7), 1550031 (2016).
- Peng, J., Wang, L., Zhao, Y., Lenci, S. Time-delay dynamics of the MR damper-cable system with one-to-one internal resonances. Nonlinear Dynamics. 105 (2), 1343-1356 (2021).
- Cha, Y. J., Agrawal, A. K., Dyke, S. J. Time delay effects on large-scale MR damper based semi-active control strategies. Smart Mater Struct. 22 (1), 015011 (2013).
- Yu, Y. et al. Experimental study of wireless structural vibration control considering different time delays. Smart Mater Struct. 24, 045005 (2015).
- Ahmadizadeh, M., Mosqueda, G., Reinhorn, A. M. Compensation of actuator delay and dynamics for real-time hybrid structural simulation. Earthq Eng Struct Dyn. 37 (1), 21-42 (2008).
- Bathaei, A., Zahrai, S. M. Compensating time delay in semi-active control of a SDOF structure with MR damper using predictive control. Struc Eng Mech. 82 (4), 445-458 (2022).
- Dyke, S. J., Spencer, Jr, B. F., Sain, M. K., Carlson, J. D. Modeling and control of magnetorheological dampers for seismic response reduction. Smart Mater Struct. 5 (5), 565-575 (1996).
- Ying, Z. G., Ni, Y. Q., Ko, J. M. A semi-active stochastic optimal control strategy for nonlinear structural systems with MR dampers. Smart Struct Syst. 5 (1), 69-79 (2009).
- Rosol, M., Martynowicz, P. Implementation of the LQG controller for a wind turbine tower-nacelle model with a MR tuned vibration absorber. J Theor App Mech-Pol. 54 (4), 1109-1123 (2016).
- Lyu, M. Z., Feng, D. C., Chen, J. B., Li, J. A decoupled approach for determination of the joint probability density function of a high-dimensional nonlinear stochastic dynamical system via the probability density evolution method. Comput Method Appl M. 418 (A), 116443 (2024).
- Chha, H., Peng, Y. Multiscale stochastic optimal control of hysteretic structures based on wavelet transform and probability density evolution method. Eng Computation. 41 (4), 865-896 (2024).
- Li, J., Peng, Y. B., Chen, J. B. A physical approach to structural stochastic optimal controls. Probabilist Eng Mech. 25 (1), 127-141 (2010).
- Peng, Y. B., Yang, J. G., Li, J. Seismic risk-based stochastic optimal control of structures using magnetorheological dampers. Nat Hazards Rev. 18 (1), B4016001 (2017).
- Dong, X. M., Yu, M., Li, Z., Liao, C., Chen, W. Neural network compensation of semi-active Control for magneto-rheological suspension with time delay uncertainty. Smart Mater Struct. 18 (1), 015014 (2008).
- Peng, Y. B., Zhang, Z. Optimal MR damper-based semiactive control scheme for strengthening seismic capacity and structural reliability. J Eng Mech. 146 (6), 04020045 (2020).
- Luo, M. X., Gao, M. Cai, G. Delayed full-state feedback control of airfoil flutter using sliding mode control method. J Fluid Struct. 61, 262-273 (2016).
- Xu, J., Chung, K. W., Chan, C. L. An efficient method for studying weak resonant double Hopf bifurcation in nonlinear systems with delayed feedbacks. Siam J Appl Dyn Syst. 6 (1), 29-60 (2007).
- Yang, J. S., Jensen, H., Chen, J. B. Structural optimization under dynamic reliability constraints utilizing probability density evolution method and metamodels in augmented input space. Struct Multidiscip Optimization. 65, 107 (2022).
- Li, J., Chen, J. B. Stochastic dynamics of structures. John Wiley & Sons, Singapore (2009).
- Peng, Y. B., Li, J. Stochastic optimal control of structures. Springer (2019).
- Dowrick, C. Beyond depression: A new approach to understanding and management. Oxford University Press (2009).
- Wang, D., Li, J. Physical random function model of ground motions for engineering purposes. Sci China Technol Sci. 54 (1), 175-182 (2011).
- Wang, D., Li, J. A random physical model of seismic ground motion field on local engineering site. Sci China Technol Sci. 55 (7), 2057-2065 (2012).
- Chen, J. B., Li, J. Strategy for selecting representative points via tangent spheres in the probability density evolution method. Int J Numer Meth Eng. 74 (13), 1988-2014 (2008).
Nachdrucke und Genehmigungen
Genehmigung beantragen, um den Text oder die Abbildungen dieses JoVE-Artikels zu verwenden
Genehmigung beantragenThis article has been published
Video Coming Soon
Copyright © 2025 MyJoVE Corporation. Alle Rechte vorbehalten