If acceleration as a function of time is known, then velocity and position functions can be derived using integral calculus. For constant acceleration, the integral equations refer to the first and second kinematic equations for velocity and position functions, respectively.
Consider an example to calculate the velocity and position from the acceleration function. A motorboat is traveling at a constant velocity of 5.0 m/s when it starts to decelerate to arrive at the dock. Its acceleration is −1/4·tm/s2. Let's determine the procedure to calculate the velocity and position function of the motorboat.
Let's take time, t = 0, when the boat starts to decelerate. Now, the velocity function can be calculated using the integral of the acceleration function

Using the expression of acceleration in the above equation, the velocity as a function of time is calculated to be

The constant of integration C1 is calculated to be 5 m/s using the value of initial time and velocity.
Hence, the velocity as a function of time reduces to

Integrating the derived velocity function with respect to time, the position function is calculated. The position as a function of time is
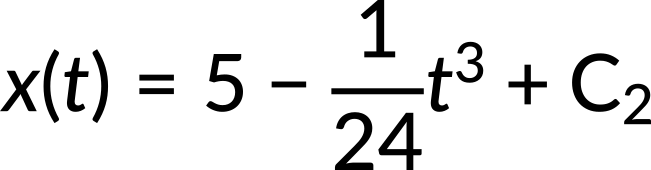
Again, using the initial conditions, the constant of integration C2 is calculated to be zero.
Thus, the position as a function of time reduces to

This text is adapted from Openstax, University Physics Volume 1, Section 3.6: Finding Velocity and Displacement from Acceleration.
Z rozdziału 3:

Now Playing
3.14 : Velocity and Position by Integral Method
Motion Along a Straight Line
5.8K Wyświetleń

3.1 : Położenie i przemieszczenie
Motion Along a Straight Line
17.0K Wyświetleń

3.2 : Średnia prędkość
Motion Along a Straight Line
17.9K Wyświetleń

3.3 : Prędkość chwilowa - I
Motion Along a Straight Line
12.2K Wyświetleń

3.4 : Prędkość chwilowa - II
Motion Along a Straight Line
9.0K Wyświetleń

3.5 : Średnie przyspieszenie
Motion Along a Straight Line
9.3K Wyświetleń

3.6 : Natychmiastowe przyspieszenie
Motion Along a Straight Line
7.5K Wyświetleń

3.7 : Równania kinematyczne - I
Motion Along a Straight Line
10.1K Wyświetleń

3.8 : Równania kinematyczne - II
Motion Along a Straight Line
9.1K Wyświetleń

3.9 : Równania kinematyczne - III
Motion Along a Straight Line
7.3K Wyświetleń

3.10 : Równania kinematyczne: rozwiązywanie problemów
Motion Along a Straight Line
11.7K Wyświetleń

3.11 : Ciała swobodnie spadające: Wprowadzenie
Motion Along a Straight Line
7.7K Wyświetleń

3.12 : Ciała swobodnie spadające: Przykład
Motion Along a Straight Line
15.3K Wyświetleń

3.13 : Prędkość i położenie metodą graficzną
Motion Along a Straight Line
7.1K Wyświetleń
Copyright © 2025 MyJoVE Corporation. Wszelkie prawa zastrzeżone