If acceleration as a function of time is known, then velocity and position functions can be derived using integral calculus. For constant acceleration, the integral equations refer to the first and second kinematic equations for velocity and position functions, respectively.

Consider an example to calculate the velocity and position from the acceleration function. A motorboat is traveling at a constant velocity of 5.0 m/s when it starts to decelerate to arrive at the dock. Its acceleration is −1/4·tm/s². Let's determine the procedure to calculate the velocity and position function of the motorboat.

Let's take time, t = 0, when the boat starts to decelerate. Now, the velocity function can be calculated using the integral of the acceleration function

Using the expression of acceleration in the above equation, the velocity as a function of time is calculated to be

The constant of integration C₁ is calculated to be 5 m/s using the value of initial time and velocity.

Hence, the velocity as a function of time reduces to

Integrating the derived velocity function with respect to time, the position function is calculated. The position as a function of time is

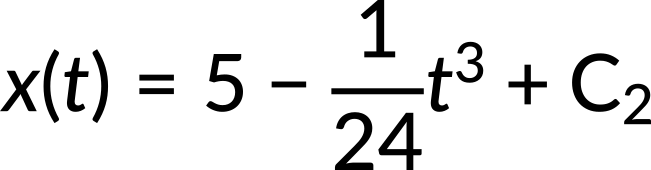
Again, using the initial conditions, the constant of integration C₂ is calculated to be zero.

Thus, the position as a function of time reduces to

This text is adapted from Openstax, University Physics Volume 1, Section 3.6: Finding Velocity and Displacement from Acceleration.