Consider an external electric field propagating through a homogeneous medium. When the electric field crosses the surface boundary of the medium, it undergoes a discontinuity. The electric field can be resolved into normal and tangential components. The amount by which the field changes at any boundary is given by the difference between the field components above and below the surface boundary.
The surface integral of an electric field is given by Gauss's law in integral form and is related to the total enclosed charge. Consider a Gaussian pillbox on the surface boundary. The surface integral of the field is the sum of the integrals over all the surfaces of the pillbox. If the thickness of the pillbox tends to zero, then the surface integral includes only the contributions of the pillbox faces above and below the boundary. Solving this gives the discontinuity of the normal component of the electric field at any surface boundary.
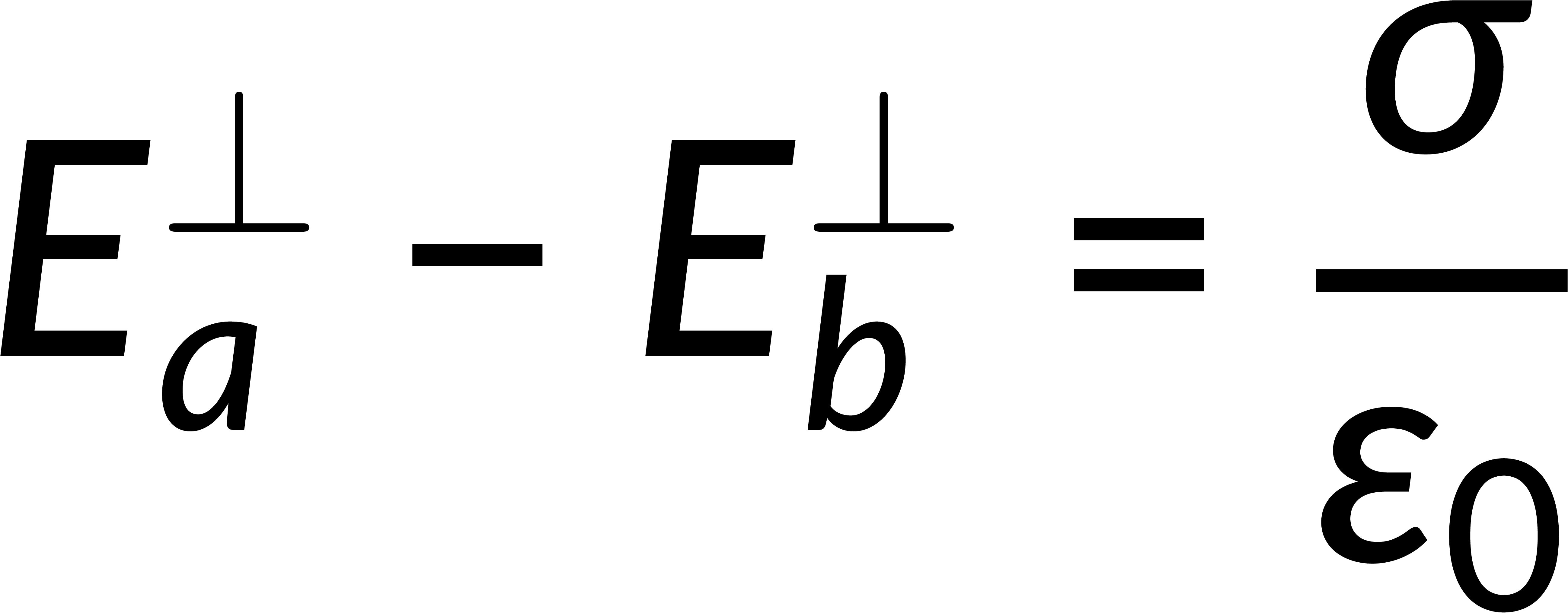
To estimate the discontinuity of the tangential component, consider a loop on the surface boundary. The integration of the electric field over this closed path is zero. Breaking this into the contributions from four parts of the loop and applying the condition that the thickness of the loop tends to zero implies that the tangential component of the electric field is continuous across the boundary.
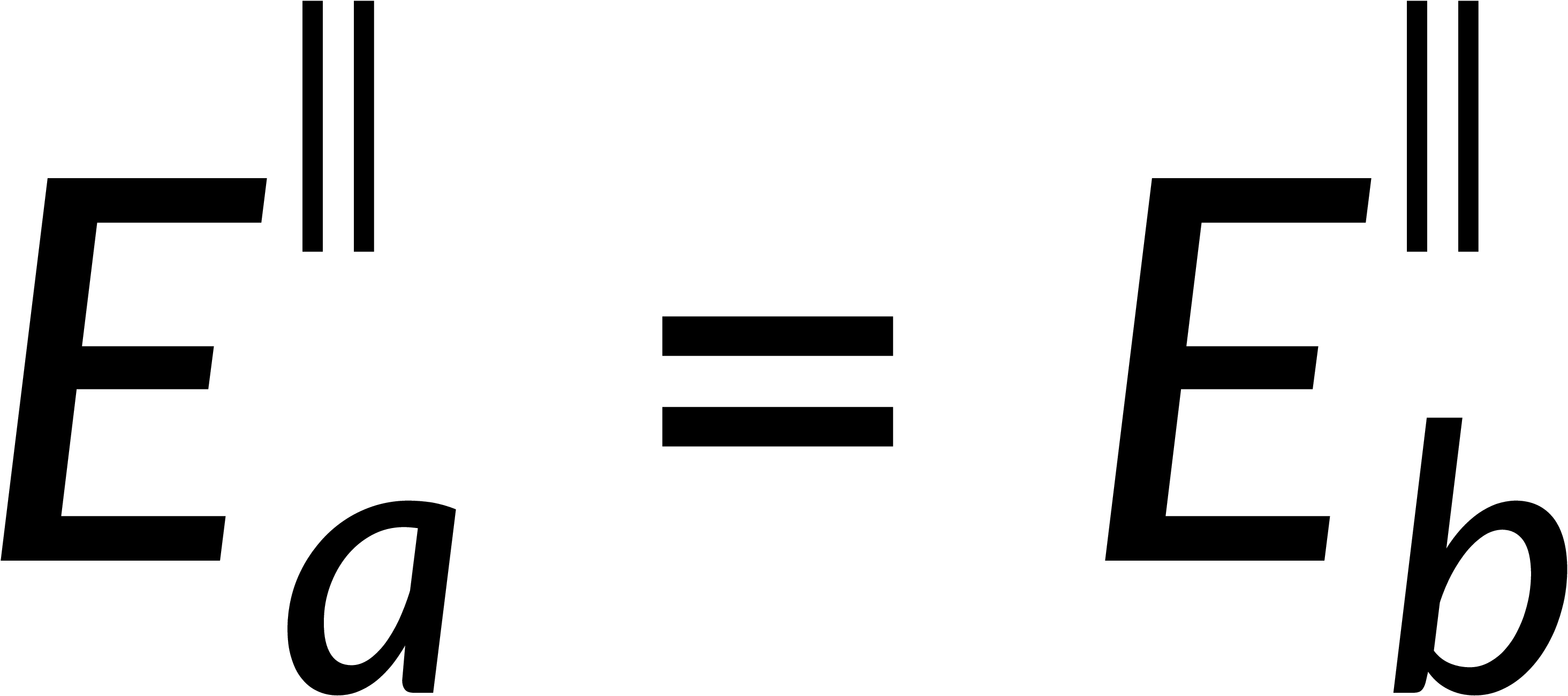
Combining the normal and tangential equations, the field at the boundary can be written by defining the unit vector perpendicular to the surface. It is known that the electric field is the negative gradient of the potential. The line integral of the field from below to above the boundary tends to zero, implying that the potential is continuous across any boundary.
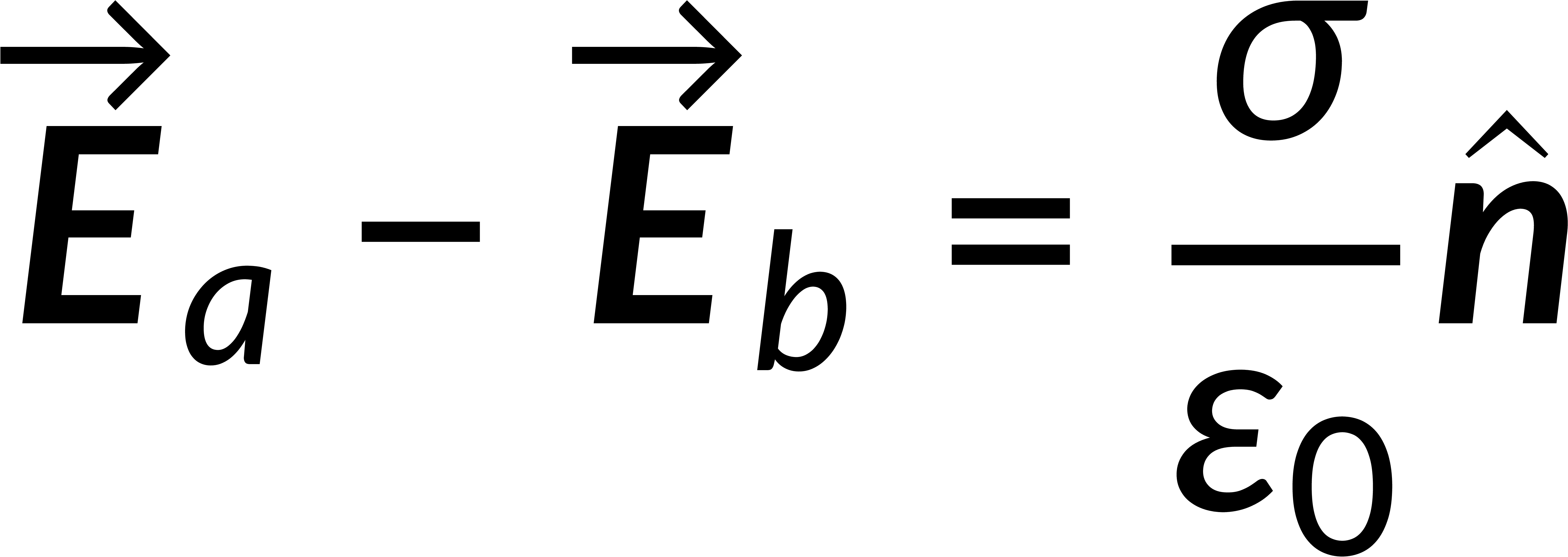
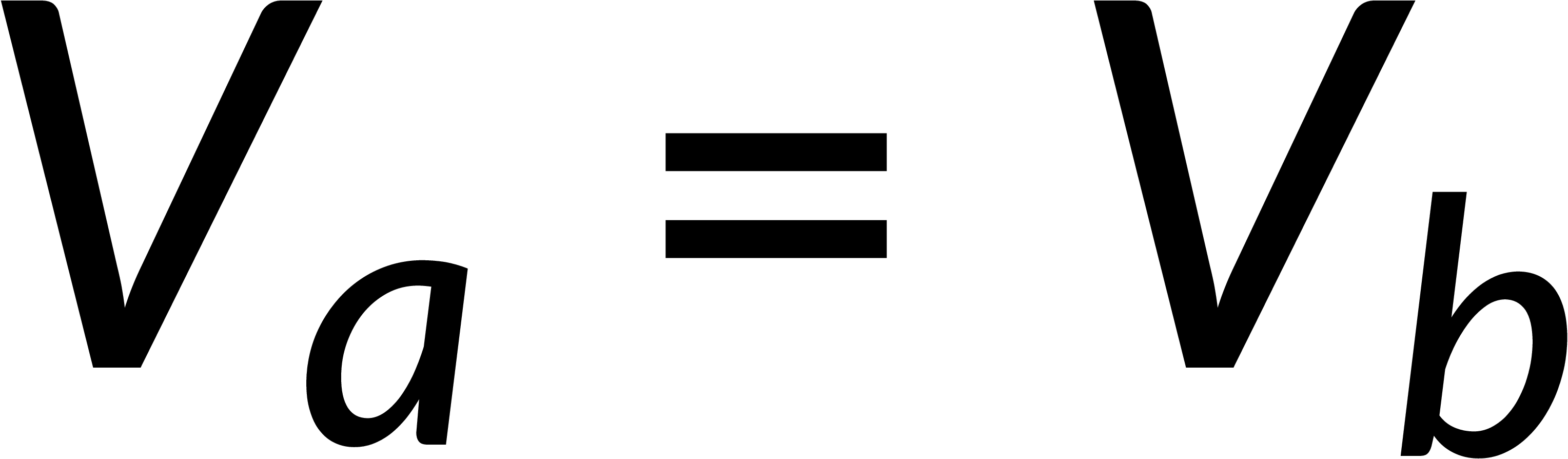
Do Capítulo 24:

Now Playing
24.14 : Condições de Contorno Eletrostáticas
Potencial elétrico
375 Visualizações

24.1 : Energia Potencial Elétrica
Potencial elétrico
5.3K Visualizações

24.2 : Energia Potencial Elétrica em um Campo Elétrico Uniforme
Potencial elétrico
4.4K Visualizações

24.3 : Energia Potencial Elétrica de duas Cargas Puntiformes
Potencial elétrico
4.3K Visualizações

24.4 : Potencial Elétrico e Diferença de Potencial
Potencial elétrico
4.1K Visualizações

24.5 : Encontrando o Potencial Elétrico a partir do Campo Elétrico
Potencial elétrico
3.9K Visualizações

24.6 : Cálculos do Potencial Elétrico I
Potencial elétrico
1.8K Visualizações

24.7 : Cálculos do Potencial Elétrico II
Potencial elétrico
1.5K Visualizações

24.8 : Superfícies Equipotenciais e Linhas de Campo
Potencial elétrico
3.5K Visualizações

24.9 : Superfícies Equipotenciais e Condutores
Potencial elétrico
3.3K Visualizações

24.10 : Determinando o Campo Elétrico a partir do Potencial Elétrico
Potencial elétrico
4.3K Visualizações

24.11 : Equações de Poisson e Laplace
Potencial elétrico
2.5K Visualizações

24.12 : Gerador de Van de Graaff
Potencial elétrico
1.6K Visualizações

24.13 : Energia Associada a uma Distribuição de Cargas
Potencial elétrico
1.4K Visualizações

24.15 : Segundo Teorema da Unicidade
Potencial elétrico
933 Visualizações
Copyright © 2025 MyJoVE Corporation. Todos os direitos reservados