Consider an external electric field propagating through a homogeneous medium. When the electric field crosses the surface boundary of the medium, it undergoes a discontinuity. The electric field can be resolved into normal and tangential components. The amount by which the field changes at any boundary is given by the difference between the field components above and below the surface boundary.
The surface integral of an electric field is given by Gauss's law in integral form and is related to the total enclosed charge. Consider a Gaussian pillbox on the surface boundary. The surface integral of the field is the sum of the integrals over all the surfaces of the pillbox. If the thickness of the pillbox tends to zero, then the surface integral includes only the contributions of the pillbox faces above and below the boundary. Solving this gives the discontinuity of the normal component of the electric field at any surface boundary.
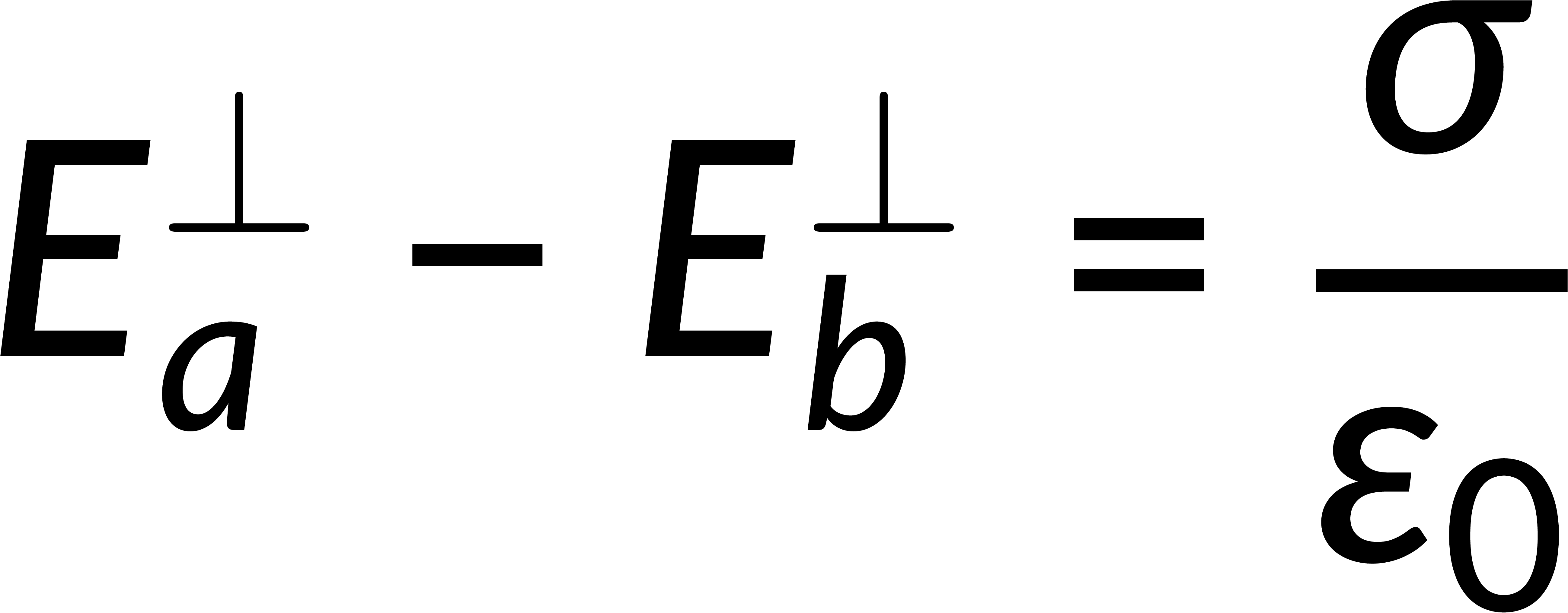
To estimate the discontinuity of the tangential component, consider a loop on the surface boundary. The integration of the electric field over this closed path is zero. Breaking this into the contributions from four parts of the loop and applying the condition that the thickness of the loop tends to zero implies that the tangential component of the electric field is continuous across the boundary.
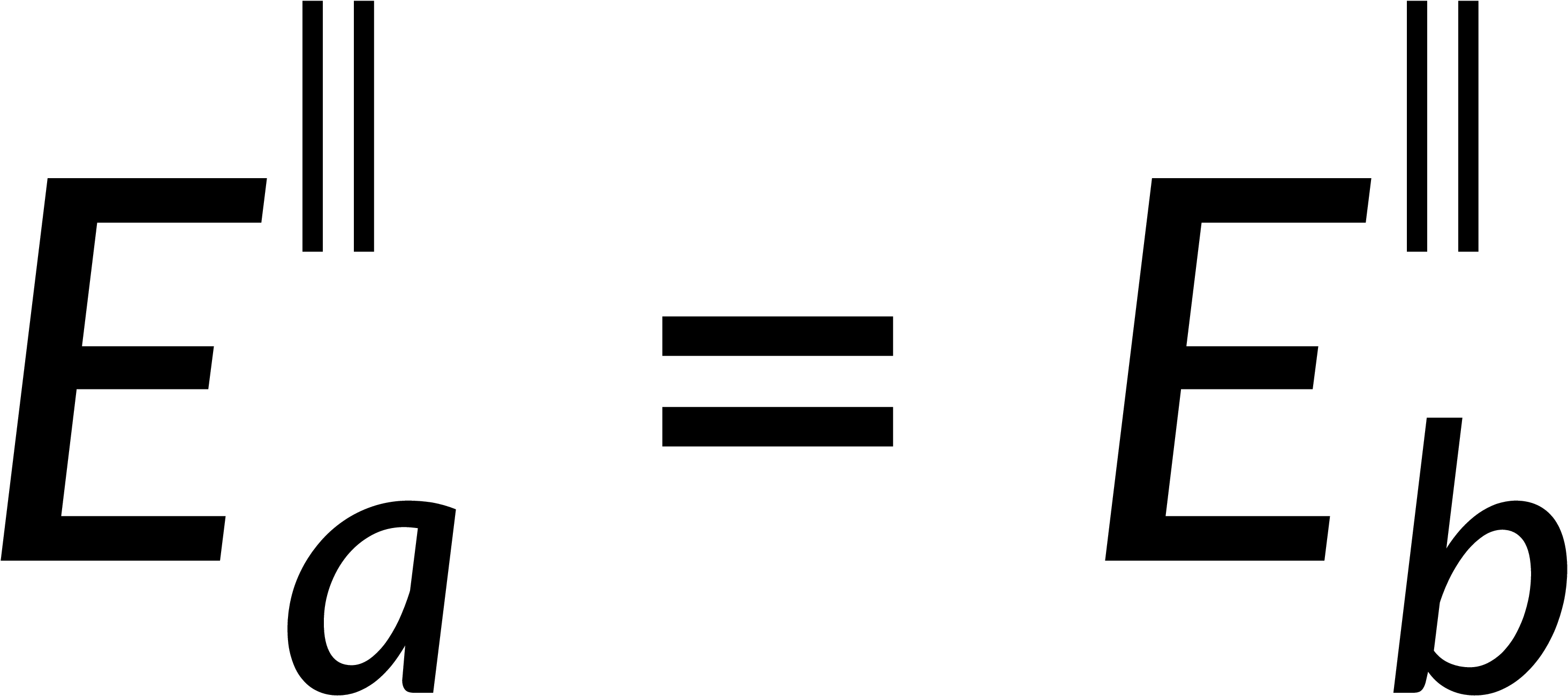
Combining the normal and tangential equations, the field at the boundary can be written by defining the unit vector perpendicular to the surface. It is known that the electric field is the negative gradient of the potential. The line integral of the field from below to above the boundary tends to zero, implying that the potential is continuous across any boundary.
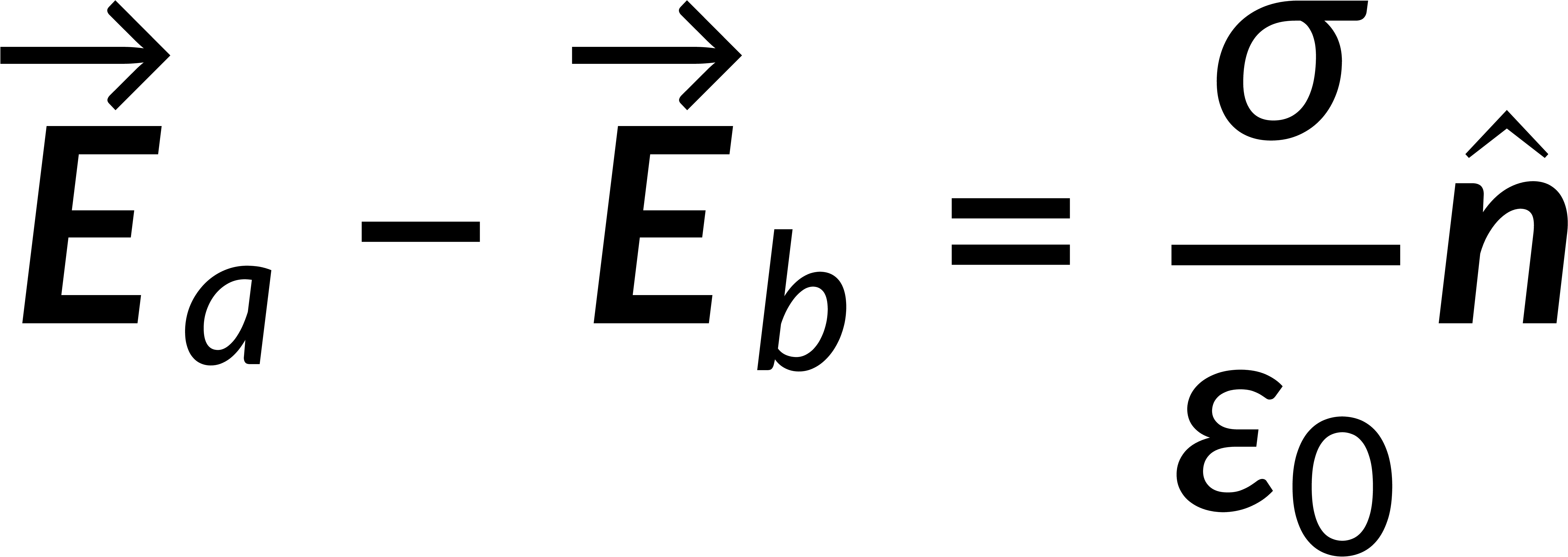
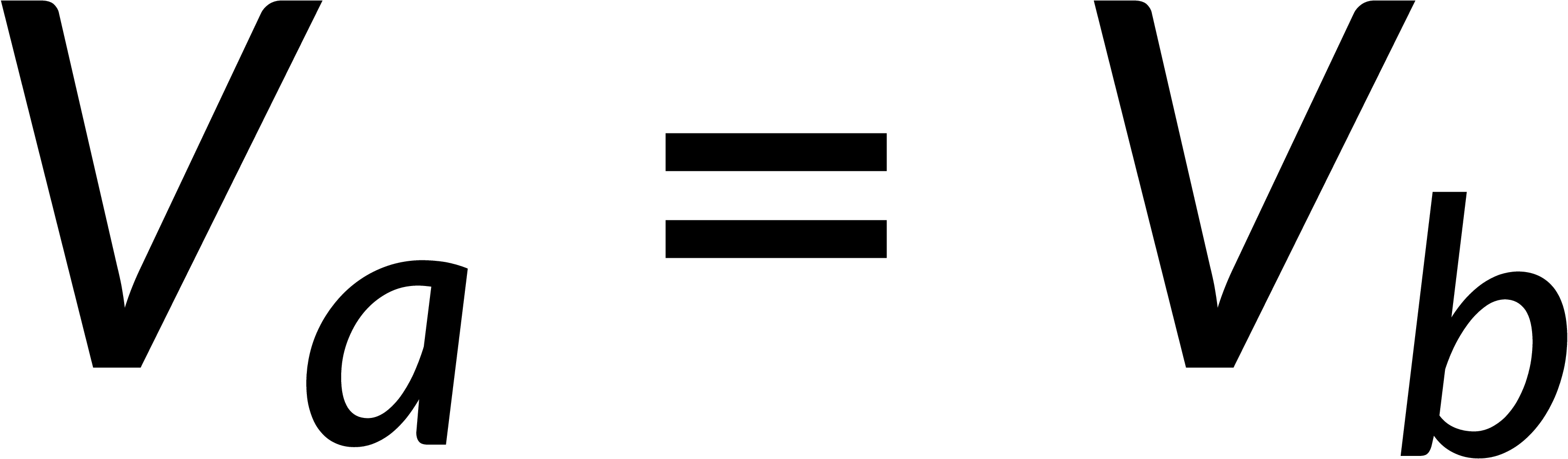
来自章节 24:

Now Playing
24.14 : Electrostatic Boundary Conditions
Electric Potential
372 Views

24.1 : 电势能
Electric Potential
5.3K Views

24.2 : 均匀电场中的电势能
Electric Potential
4.3K Views

24.3 : 两点电荷的势能
Electric Potential
4.3K Views

24.4 : 电位和电位差
Electric Potential
4.1K Views

24.5 : 从电场中寻找电势
Electric Potential
3.9K Views

24.6 : 电势 I 的计算
Electric Potential
1.8K Views

24.7 : 电势计算 II
Electric Potential
1.5K Views

24.8 : 等势面和磁力线
Electric Potential
3.5K Views

24.9 : 等电位表面和导体
Electric Potential
3.3K Views

24.10 : 根据电势确定电场
Electric Potential
4.3K Views

24.11 : 泊松和拉普拉斯方程
Electric Potential
2.5K Views

24.12 : Van de Graaff 生成器
Electric Potential
1.6K Views

24.13 : 与电荷分布相关的能量
Electric Potential
1.4K Views

24.15 : 第二唯一性定理
Electric Potential
931 Views
版权所属 © 2025 MyJoVE 公司版权所有,本公司不涉及任何医疗业务和医疗服务。