A buffer can prevent a sudden drop or increase in the pH of a solution after the addition of a strong acid or base up to its buffering capacity; however, such addition of a strong acid or base does result in the slight pH change of the solution. The small pH change can be calculated by determining the resulting change in the concentration of buffer components, i.e., a weak acid and its conjugate base or vice versa. The concentrations obtained using these stoichiometric calculations can be used to determine the solution’s final pH using the Henderson-Hasselbalch equation or an ICE table.
For example, a buffered solution contains 0.65 mol of formic acid and sodium formate. As the concentration of the weak acid and its conjugate base is the same here, the solution’s pH is equal to the pKa of the weak acid, which is 3.74 in this case. If 0.05 mol HNO3 is added into this solution, the resultant changes in the concentration of the formic acid and sodium formate can be determined by stoichiometric calculations as shown in the table below.
| H+ (aq) | HCOO− (aq) | HCOOH (aq) | |
| Before addition (M) | ~0.00 mol | 0.65 mol | 0.65 mol |
| Addition (M) | 0.050 mol | - | - |
| After addition (M) | ~0.00 mol | 0.60 mol | 0.70 mol |
The solution’s final pH can then be determined by plugging in changed concentrations of formic acid and sodium formate into the Henderson-Hasselbalch equation.
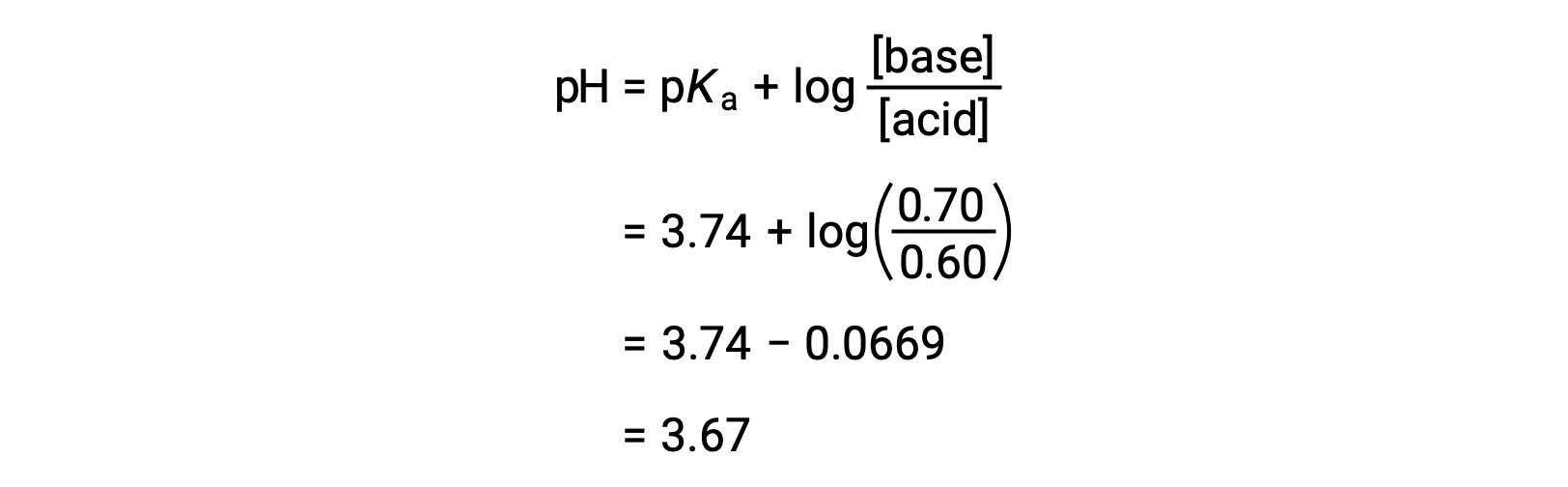
Thus, the addition of 0.05 mol of HNO3 reduces the pH of the solution from 3.74 to 3.67.
Similarly, if 0.10 mol NaOH is added into the same solution, the resultant changes in the concentration of the formic acid and sodium formate can be determined by stoichiometric calculations as shown in the table below.
| OH− (aq) | HCOOH (aq) | HCOO− (aq) | H2O (l) | |
| Before addition (M) | ~0.00 mol | 0.65 mol | 0.65 mol | - |
| Addition (M) | 0.10 mol | - | - | - |
| After addition (M) | ~0.00 mol | 0.55 mol | 0.75 mol | - |
The final pH of the solution can then be determined by plugging in changed concentrations of formic acid and sodium formate into the Henderson-Hasselbalch equation.

Thus, the addition of 0.10 mol NaOH increases the pH of the solution from 3.74 to 3.87.
Z rozdziału 16:

Now Playing
16.4 : Calculating pH Changes in a Buffer Solution
Acid-base and Solubility Equilibria
52.2K Wyświetleń

16.1 : Wspólny efekt jonowy
Acid-base and Solubility Equilibria
40.6K Wyświetleń

16.2 : Buffers
Acid-base and Solubility Equilibria
162.9K Wyświetleń

16.3 : Równanie Hendersona-Hasselbalcha
Acid-base and Solubility Equilibria
67.5K Wyświetleń

16.5 : Skuteczność bufora
Acid-base and Solubility Equilibria
48.1K Wyświetleń

16.6 : Obliczenia miareczkowania: mocny kwas - mocna zasada
Acid-base and Solubility Equilibria
28.7K Wyświetleń

16.7 : Obliczenia miareczkowania: słaby kwas - mocna zasada
Acid-base and Solubility Equilibria
43.2K Wyświetleń

16.8 : Wskaźniki
Acid-base and Solubility Equilibria
47.5K Wyświetleń

16.9 : Miareczkowanie kwasu poliprotonowego
Acid-base and Solubility Equilibria
95.3K Wyświetleń

16.10 : Równowaga rozpuszczalności
Acid-base and Solubility Equilibria
51.0K Wyświetleń

16.11 : Czynniki wpływające na rozpuszczalność
Acid-base and Solubility Equilibria
32.7K Wyświetleń

16.12 : Powstawanie jonów złożonych
Acid-base and Solubility Equilibria
22.9K Wyświetleń

16.13 : Wytrącanie jonów
Acid-base and Solubility Equilibria
27.3K Wyświetleń

16.14 : Analiza jakościowa
Acid-base and Solubility Equilibria
19.7K Wyświetleń

16.15 : Krzywe miareczkowania kwasowo-zasadowego
Acid-base and Solubility Equilibria
125.3K Wyświetleń
Copyright © 2025 MyJoVE Corporation. Wszelkie prawa zastrzeżone