Arrhenius denklemi, kimyasal reaksiyonlar için aktivasyon enerjisi ve hız sabiti k'yi ilişkilendirir.Arrhenius denkleminde, k = Ae^−Ea/RT, R, R 8.314 J / mol·K değerine sahip ideal gaz sabitidir, T kelvin ölçeğindeki sıcaklık, E_a J / mol cinsinden aktivasyon enerjisidir. e, 2.7183 sabitidir ve A, çarpışmaların sıklığı ve reaksiyona giren moleküllerin yönelimi ile ilgili olan ve frekans faktörü olarak adlandırılan bir sabittir.

Arrhenius denklemi, deneysel kinetik verilerden bir reaksiyonun aktivasyon enerjisini hesaplamak için kullanılabilir. Bir reaksiyon için E_a'nın belirlenmesine yönelik uygun bir yaklaşım, k'nın iki veya daha fazla farklı sıcaklıkta ölçülmesini içerir. Doğrusal bir denklem şeklini alan Arrhenius denkleminin değiştirilmiş bir versiyonunu kullanır:

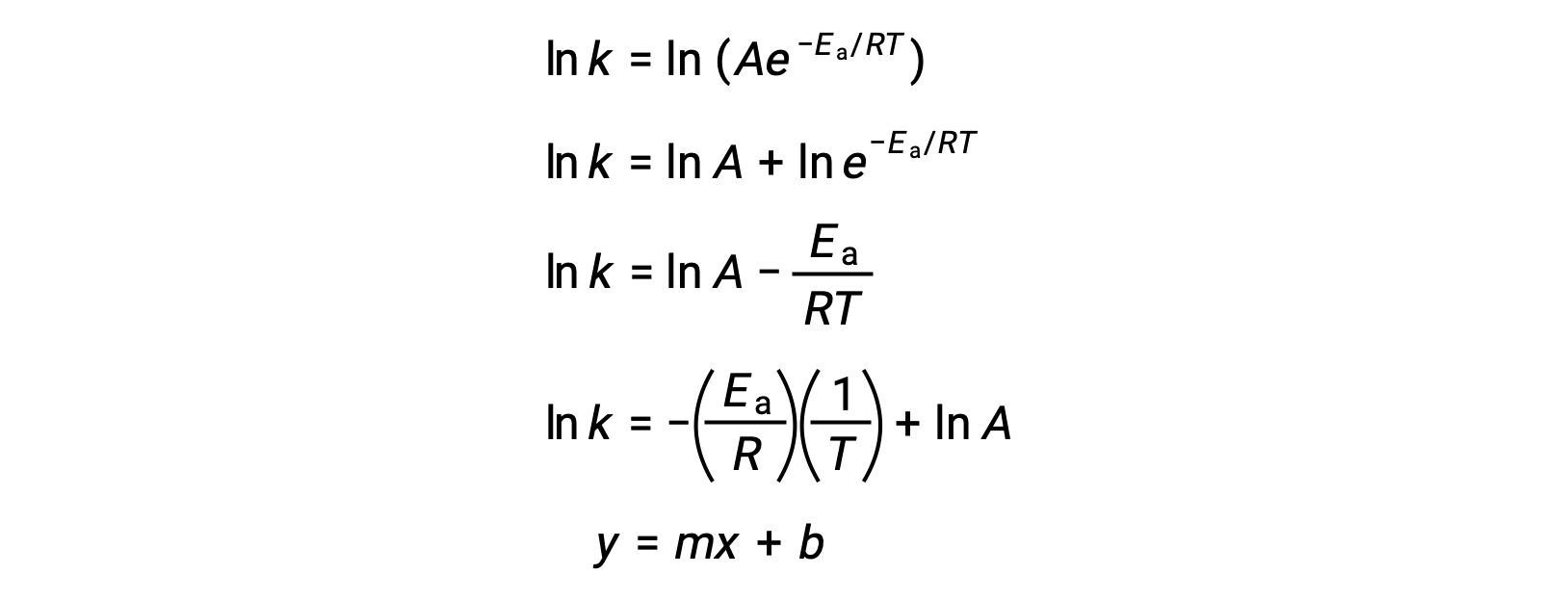
1/T'ye karşılık lnk'nin bir grafiği doğrusaldır ve eğimi −E_a/R 'ye eşittir ve y kesme noktası lnA'ya eşittir.

Şu reaksiyonu düşünün:

Bu reaksiyonun aktivasyon enerjisi, sıcaklık ile hız sabitindeki değişim gösterildiği gibi reaksiyon kinetik verilerinden biliniyorsa belirlenebilir.

Sıcaklık (K)	Hız sabiti (L/mol/s)
555	3,52 × 10–7
575	1,22 × 10–6
645	8,59 × 10–5
700	1,16 × 10–3
781	3,95× 10–2

Sağlanan veriler, sıcaklığın tersi (1/T) ve doğal log k (ln k)değerlerini türetmek için kullanılabilir.

1/T (K–1)	ln k
1,80 × 10–3	–14,860
1,74 × 10–3	–13,617
1,55 × 10–3	–9,362
1,43 × 10–3	–6,759
1,28 × 10–3	–3,231

Türetilmiş veri noktalarının 1/T'ye karşı ln k ile grafiğini çizerken, gösterildiği gibi lnk ve 1/Tarasında doğrusal bir ilişki sergileyen bir çizgi grafiği oluşturulur.

Aktivasyon enerjisine karşılık gelen çizginin eğimi, deneysel veri çiftlerinden herhangi ikisi kullanılarak tahmin edilebilir.

Aktivasyon enerjisinin türetilmesinde alternatif bir yaklaşım, iki farklı sıcaklıkta hız sabitinin kullanılmasını içerir. Bu yaklaşımda, Arrhenius denklemi iki noktalı uygun bir biçimde yeniden düzenlenir:

Denklemi yeniden düzenlerken, aktivasyon enerjisi için bir ifade üretilir.

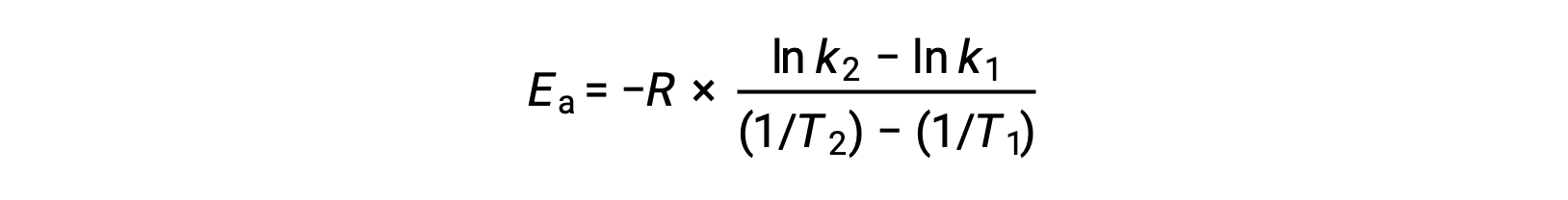
Herhangi iki veri çiftini ikame ederek ve ileri hesaplamalar, mol başına joule veya mol başına kilojoule cinsinden aktivasyon enerjisi değerini verir.

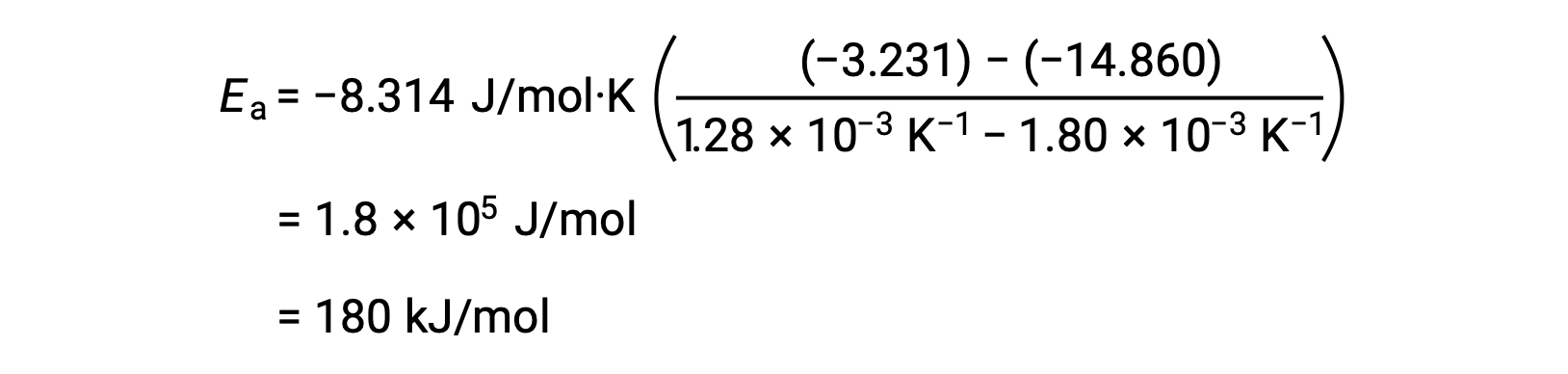
Bu alternatif iki noktalı yaklaşım, grafiksel yaklaşımla aynı sonucu verir. Bununla birlikte, pratikte, grafiksel yaklaşım, gerçek deneysel verilerle çalışırken tipik olarak daha güvenilir sonuçlar sağlar.

Bu metin bu kaynaktan uyarlanmıştır Openstax, Chemistry 2e, Section 12.5: Collision Theory.