29.5 : Magnetic Field Due to Two Straight Wires
Consider two parallel straight wires carrying a current of 10 A and 20 A in the same direction and separated by a distance of 20 cm. Calculate the magnetic field at a point "P2", midway between the wires. Also, evaluate the magnetic field when the direction of the current is reversed in the second wire.
The current flowing in the wires and the separation distance between the wires are the known quantities. The magnetic field at a point 10 cm from each wire must be evaluated.
The magnetic field lines form counterclockwise concentric circles around the wires. The expression for the magnetic field due to wire 1 and wire 2 is given by,
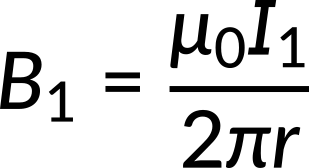
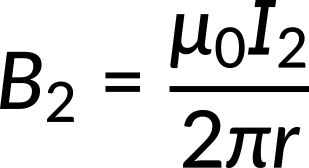
The magnetic fields due to both the current-carrying wires point in opposite directions at the midpoint between both wires. According to the principle of magnetic field superposition, the net magnetic field due to multiple conductors is the vector sum of the field due to the individual conductors. Thus, the net magnetic field is the difference between the magnetic fields for both wires. When the expression for the magnetic field for the individual wires is substituted, the net magnetic field expression reduces to,

After substituting the current and distance values, the net magnetic field is calculated as −2 x 10−5 T when the current flows in the same direction in both wires.
When the current direction is reversed in the second wire, the magnetic fields due to both wires point in the same direction at the midpoint. Therefore, applying the principle of magnetic field superposition, the net magnetic field at the midpoint is expressed as,

After substituting the current and distance values, the net magnetic field is calculated as 6 x 10−5 T when the current flows in opposite directions in both wires.
장에서 29:

Now Playing
29.5 : Magnetic Field Due to Two Straight Wires
Sources of Magnetic Fields
2.4K Views

29.1 : 움직이는 전하로 인한 자기장
Sources of Magnetic Fields
8.4K Views

29.2 : 비오-사바트 법칙
Sources of Magnetic Fields
5.8K Views

29.3 : Biot-Savart Law: 문제 해결
Sources of Magnetic Fields
2.5K Views

29.4 : 얇은 직선 와이어로 인한 자기장
Sources of Magnetic Fields
4.7K Views

29.6 : 두 개의 병렬 전류 사이의 자기력
Sources of Magnetic Fields
3.5K Views

29.7 : 전류 루프의 자기장
Sources of Magnetic Fields
4.4K Views

29.8 : 자기장의 발산(Divergence and Curl)
Sources of Magnetic Fields
2.8K Views

29.9 : 암페어의 법칙
Sources of Magnetic Fields
3.7K Views

29.10 : 암페어의 법칙: 문제 해결
Sources of Magnetic Fields
3.5K Views

29.11 : 솔레노이드
Sources of Magnetic Fields
2.5K Views

29.12 : 솔레노이드의 자기장
Sources of Magnetic Fields
3.8K Views

29.13 : 토로이드
Sources of Magnetic Fields
2.9K Views

29.14 : 자기 벡터 전위
Sources of Magnetic Fields
546 Views

29.15 : 자화된 물체로 인한 전위
Sources of Magnetic Fields
259 Views
See More
Copyright © 2025 MyJoVE Corporation. 판권 소유