The magnetic field due to a volume current distribution given by the Biot–Savart Law can be expressed as follows:

To evaluate the divergence of the magnetic field, the divergence is applied to both sides of the Biot–Savart equation:
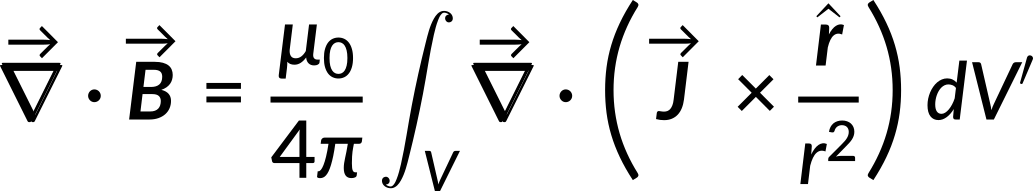
Applying the vector product rule, the term within the integral is simplified to the following equation:
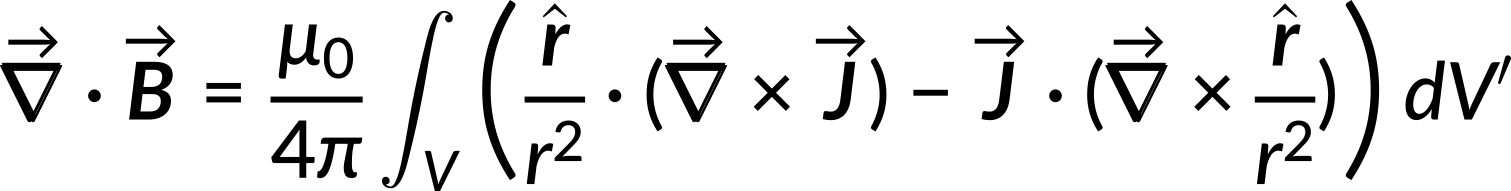
The first term involving the curl of the current density function is zero since the current density is independent of the field coordinates. Using vector analysis, the second term in the above equation also reduces to zero. Hence, the divergence of a magnetic field is zero:
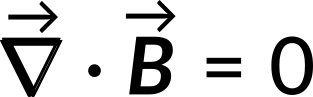
The zero divergence of the magnetic field is valid for any field, irrespective of whether the field is static or time-dependent. This equation states that the magnetic flux that passes through an arbitrary closed surface is zero. This is possible only if the number of magnetic field lines that enter the closed surface equals the number of field lines that exit through this closed surface. Thus, magnetic field lines always form closed loops. It also implies that magnetic monopoles do not exist.
To evaluate the curl of the magnetic field, the curl is applied to both sides of the Biot–Savart equation:

Again, by applying vector analysis, the equation is simplified:
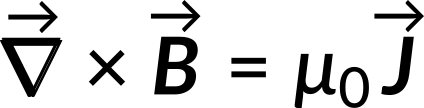
The curl of the magnetic field equals the vacuum permeability multiplied by the current density. The same result is obtained by applying Stoke's theorem to the integral form of Ampere's Law:

Since the above relation holds for any closed loop, the integrands are equal. This equation is called the differential form of Ampere's Law.
章から 29:

Now Playing
29.8 : Divergence and Curl of Magnetic Field
磁場の発生源
2.7K 閲覧数

29.1 : 移動電荷による磁場
磁場の発生源
8.2K 閲覧数

29.2 : ビオ・サバール法
磁場の発生源
5.6K 閲覧数

29.3 : ビオ・サバールの法則:問題解決
磁場の発生源
2.4K 閲覧数

29.4 : 細い直線ワイヤーによる磁場
磁場の発生源
4.6K 閲覧数

29.5 : 2本の直線ワイヤによる磁場
磁場の発生源
2.3K 閲覧数

29.6 : 2つの並列電流間の磁力
磁場の発生源
3.4K 閲覧数

29.7 : 電流ループの磁場
磁場の発生源
4.2K 閲覧数

29.9 : アンペアの法則
磁場の発生源
3.6K 閲覧数

29.10 : アンペアの法則:問題解決
磁場の発生源
3.5K 閲覧数

29.11 : ソレノイド
磁場の発生源
2.4K 閲覧数

29.12 : ソレノイドの磁場
磁場の発生源
3.6K 閲覧数

29.13 : トロイド
磁場の発生源
2.8K 閲覧数

29.14 : 磁気ベクトルポテンシャル
磁場の発生源
488 閲覧数

29.15 : 磁化された物体による電位
磁場の発生源
243 閲覧数
See More
Copyright © 2023 MyJoVE Corporation. All rights reserved