26.11 : Boundary Conditions for Current Density
Current density becomes discontinuous across an interface of materials with different electrical conductivities. The normal component of the current density is continuous across the boundary.
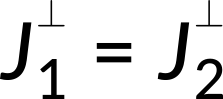
However, the tangential components of the current density are discontinuous across the interface.

Consider an interface separated by two conducting media with conductivities σ1 and σ2. The steady current density at the interface is ![]() , in medium 1 at a point P1. It makes an angle α1 with the normal. The current density
, in medium 1 at a point P1. It makes an angle α1 with the normal. The current density ![]() at point P2 in medium 2 makes an angle α2 with the normal.
at point P2 in medium 2 makes an angle α2 with the normal.
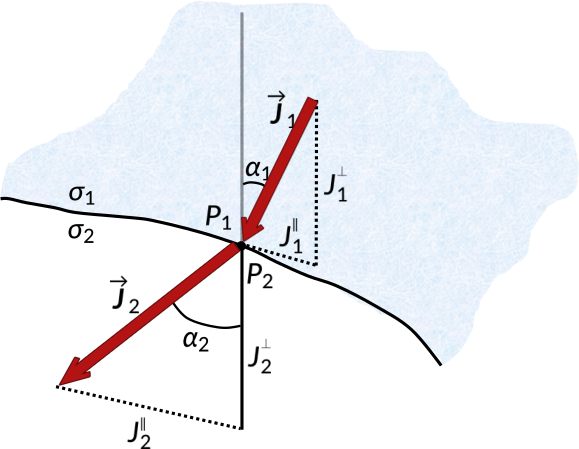
The normal and tangential components of the current density give the equations as follows:
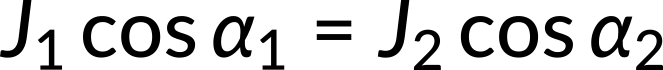
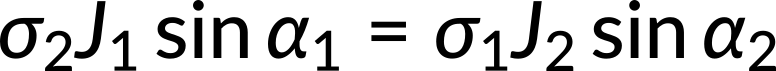
Taking the ratio of the two equations, the expression for the electrical conductivities in both the media is obtained.
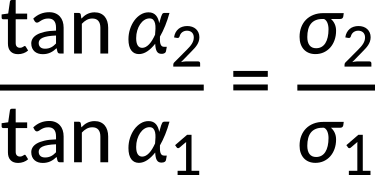
If the electrical conductivity of medium 1 is greater than that of medium 2, the angle α2 approaches zero. This implies that the current density ![]() is normal to the surface of conductor 1.
is normal to the surface of conductor 1.
章から 26:

Now Playing
26.11 : Boundary Conditions for Current Density
電流と抵抗
778 閲覧数

26.1 : 電流
電流と抵抗
5.6K 閲覧数

26.2 : ドリフト速度
電流と抵抗
4.0K 閲覧数

26.3 : 電流密度
電流と抵抗
3.8K 閲覧数

26.4 : 比 抵抗
電流と抵抗
3.3K 閲覧数

26.5 : 抵抗
電流と抵抗
4.3K 閲覧数

26.6 : オームの法則
電流と抵抗
5.4K 閲覧数

26.7 : 非オーミックデバイス
電流と抵抗
1.0K 閲覧数

26.8 : 電力
電流と抵抗
3.0K 閲覧数

26.9 : 電気エネルギー
電流と抵抗
1.2K 閲覧数

26.10 : 連続方程式
電流と抵抗
781 閲覧数

26.12 : 電気伝導率
電流と抵抗
1.1K 閲覧数

26.13 : 金属伝導の理論
電流と抵抗
1.3K 閲覧数
Copyright © 2023 MyJoVE Corporation. All rights reserved