16.12 : 錯体イオンの形成
ルイス酸塩基化学の一種である錯体イオン(または配位錯体)は、中心原子(典型的には遷移金属陽イオン)が配位子と呼ばれるイオンや分子に囲まれて構成されたものです。これらの配位子は、H2OやNH3のような中性分子であったり、CN−やOH−のようなイオンの場合もあります。多くの場合、配位子はルイス塩基として働き、中心原子に一対の電子を供与します。このようなルイス酸塩基反応は、配位化学と呼ばれる幅広い分野の一例であり、この記事の別の章のテーマでも紹介しています。
金属イオンが1つ以上の配位子と反応して配位錯体を形成する際の平衡定数を生成定数(Kf)と呼ぶ(安定定数と呼ばれることもある)。例えば、錯体イオン[Cu(CN)2]−は次のような反応で生成します。

この反応の生成定数は、

また、逆の反応(錯イオンの分解)も考えられ、その場合の平衡定数は解離定数(Kd)と呼ばれます。前述の相互反応における平衡定数の関係のように、解離定数は生成定数の逆数です。(Kd=Kf−1)
錯イオン形成による溶解の例として、塩化銀と水の混合物にアンモニア水を加えた場合を考えましょう。塩化銀は水にわずかに溶解し、わずかな濃度のAg+([Ag+]=1.3 × 10−5 M)が得られます。
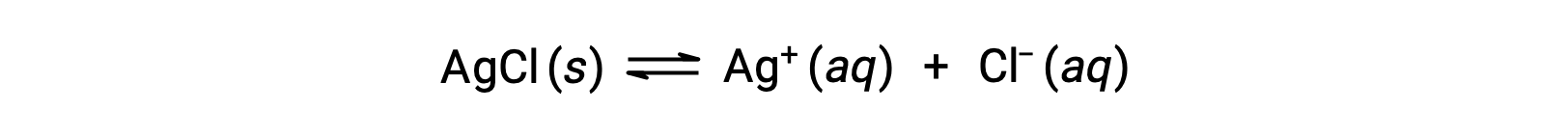
しかし、水中にNH3が存在すると、次式に従って錯イオンである[Ag(NH3)2]+が形成されます。
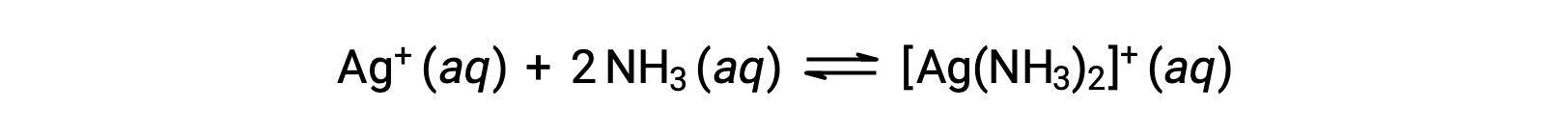
上記の文章は以下から引用しました。Openstax, Chemistry 2e, Section 15.2: Lewis Acids and Bases.
章から 16:

Now Playing
16.12 : 錯体イオンの形成
酸塩基と溶解度平衡
23.4K 閲覧数

16.1 : 共通イオン効果
酸塩基と溶解度平衡
41.1K 閲覧数

16.2 : 緩衝液
酸塩基と溶解度平衡
163.7K 閲覧数

16.3 : ヘンダーソン-ハッセルバルヒ式
酸塩基と溶解度平衡
68.4K 閲覧数

16.4 : 緩衝液中のpHの変化の計算
酸塩基と溶解度平衡
52.8K 閲覧数

16.5 : 緩衝液の有効性
酸塩基と溶解度平衡
48.6K 閲覧数

16.6 : 滴定計算:強酸-強塩基
酸塩基と溶解度平衡
29.2K 閲覧数

16.7 : 滴定計算:弱酸-弱塩基
酸塩基と溶解度平衡
43.9K 閲覧数

16.8 : 指示薬
酸塩基と溶解度平衡
48.0K 閲覧数

16.9 : 多価酸の滴定
酸塩基と溶解度平衡
95.9K 閲覧数

16.10 : 溶解平衡
酸塩基と溶解度平衡
52.2K 閲覧数

16.11 : 溶解性に影響する因子
酸塩基と溶解度平衡
33.2K 閲覧数

16.13 : イオンの沈殿
酸塩基と溶解度平衡
27.7K 閲覧数

16.14 : 定性分析
酸塩基と溶解度平衡
22.0K 閲覧数

16.15 : 酸塩基滴定曲線
酸塩基と溶解度平衡
126.8K 閲覧数
Copyright © 2023 MyJoVE Corporation. All rights reserved