29.15 : Potential Due to a Magnetized Object

Magnetic dipoles in magnetic materials are aligned when placed under an external magnetic field. For paramagnets and ferromagnets, dipole alignment occurs in the direction of the magnetic field. However, the dipoles align opposite to the field in the case of diamagnets. This state of magnetic polarization due to the external field is called magnetization. Magnetization is defined as the dipole moment per unit volume. It plays a similar role to polarization in electrostatics.

The vector potential due to a single magnetic dipole at a field point is given by,

The vector potential can be rewritten in terms of magnetization for a magnetized material with aligned dipole moments.

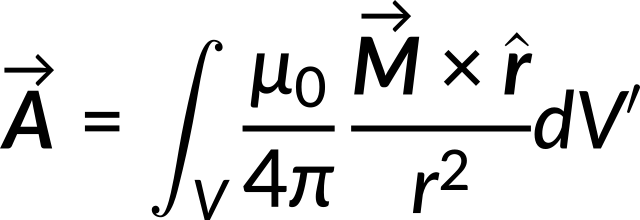
The equation becomes simplified using vector analysis.

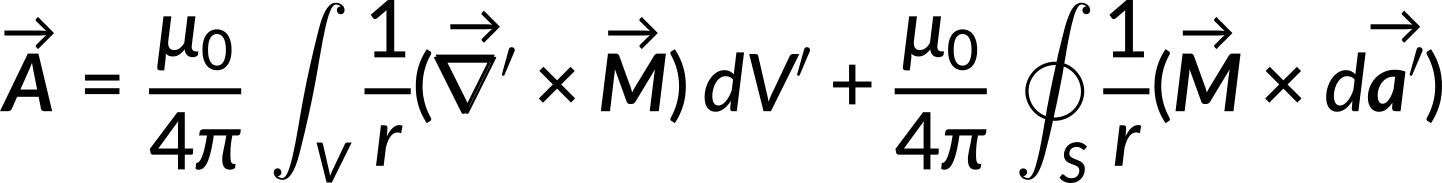
The first term in the above expression is the potential due to the volume current, while the second term is the potential due to the surface current.

Now, the volume current is defined as the curl of the magnetization vector. The surface current is defined as the cross product of the magnetization vector and the unit vector along the area vector. By substituting the expressions for the volume and surface currents, the potential expression reduces to,

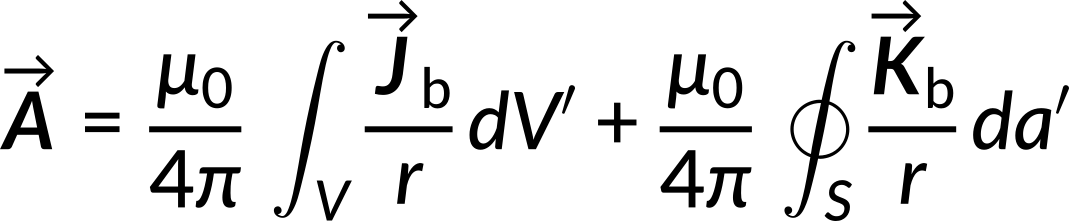
This expression bears an analogy with an electrostatic case, where the field of a polarized object constitutes the field due to bound volume and surface charges.

If the applied magnetic field is uniform, the volume currents become zero, and only the surface current at the boundary of the material exists. When the field applied is non-uniform, the volume currents persist.

Like any steady current, the bound volume current obeys the conservation law. The bound volume current divergence is zero since the divergence of a curl is zero.