16.3 : Equations of Wave Motion
Mathematically, the motion of a wave can be studied using a wavefunction. Consider a string oscillating up and down in simple harmonic motion, having a period T. The wave on the string is sinusoidal and is translated in the positive x-direction as time progresses. Sine is a function of the angle θ, oscillating between +A and −A and repeating every 2π radians. To construct a wave model, the ratio of the angle θ and the position x is considered.

From the ratio, using the value of θ, and multiplying the sine function with amplitude A, we can model the y-position of the string as a function of position x.

The wave on the string travels with a constant velocity and moves a distance equal to vt in time t, so we can modify the wave function using this. Further, multiplying by the term 2π/λ simplifies the equation.
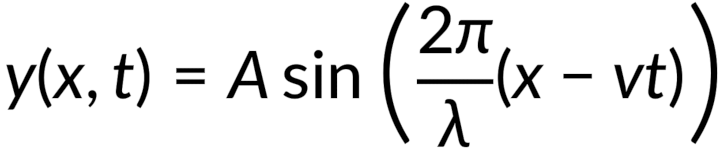
Recall the expressions for wave number and angular frequency, which modify the first and second terms of the above equation, respectively. Hence the reduced expression for the wavefunction of a simple harmonic wave on a string is obtained.
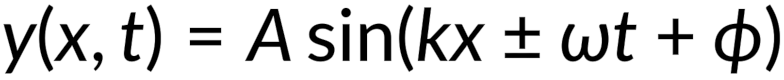
An angle φ that corresponds to the initial phase of the wave is added to the wave function. It is an indicator of the initial position of the particle just before the start of wave motion and is used to determine various wave parameters.
This text is adapted from Openstax, University Physics Volume 1, Section 16.2: Mathematics of Waves.
Dal capitolo 16:

Now Playing
16.3 : Equations of Wave Motion
Waves
5.6K Visualizzazioni

16.1 : Onde in viaggio
Waves
5.1K Visualizzazioni

16.2 : Parametri dell'onda
Waves
7.6K Visualizzazioni

16.4 : Rappresentazione grafica della funzione d'onda
Waves
1.6K Visualizzazioni

16.5 : Velocità e accelerazione di un'onda
Waves
3.8K Visualizzazioni

16.6 : Velocità di un'onda trasversale
Waves
1.5K Visualizzazioni

16.7 : Risoluzione dei problemi: accordatura di una corda di chitarra
Waves
399 Visualizzazioni

16.8 : Energia cinetica e potenziale di un'onda
Waves
3.6K Visualizzazioni

16.9 : Energia e potenza di un'onda
Waves
3.5K Visualizzazioni

16.10 : Interferenza e sovrapposizione delle onde
Waves
4.8K Visualizzazioni

16.11 : Riflessione delle onde
Waves
3.7K Visualizzazioni

16.12 : Propagazione delle onde
Waves
2.3K Visualizzazioni

16.13 : Onde stazionarie
Waves
4.4K Visualizzazioni

16.14 : Modalità delle onde stazionarie - I
Waves
2.8K Visualizzazioni

16.15 : Modalità delle onde stazionarie: II
Waves
826 Visualizzazioni